Электрохимическая катодная защита (КЗ) является важнейшим средством продления срока службы подземных металлических конструкций, в том числе нефте- и газопроводов. КЗ основана на смещении электрического потенциала защищаемого объекта в отрицательную область относительно потенциала грунта. Постоянное электрическое поле в системе «анод–грунт–защищаемое сооружение» создается катодной станцией с помощью анодных заземлителей, погруженных в грунт. В практике КЗ применяются различные типы заземлителей: гибкие протяженные аноды, длиной в десятки километров, прокладываемые вдоль магистральных трубопроводов при их первичной укладке [1, 5]; глубинные аноды, соединенные из отдельных анодных блоков в «гирлянду», опущенную в вертикальную скважину [6, 7] и другие.
Для обеспечения эффективной защиты от коррозии необходимо, чтобы потенциал металла трубы относительно грунта находился в заданном интервале: при его сдвиге в положительную сторону эффективность КЗ снижается; при смещении в отрицательную сторону возникает «эффект перезащиты», что приводит к повышенному расходу электроэнергии, усиленному газообразованию на поверхности металла, отслоению и преждевременному износу изоляции трубопровода [7, 8].
В начальный период эксплуатации поверхностное сопротивление изоляции имеет максимальное значение и может достигать 300000 Ом·м2. С течением времени этот показатель непрерывно падает под действием влияния грунтовых вод, перепадов температуры и других внешних факторов. В этих условиях для обеспечения эффективной защиты необходимо соответствующее повышение напряжения катодной станции, и как следствие, – увеличение плотности тока, стекающего с анода в грунт. В свою очередь, превышение предельной плотности тока приводит к интенсивному растворению анодного материала, и тем самым к сокращению срока службы анода [4, 5]. Локальные повреждения (дефекты) в изоляции трубопровода возникают, как правило, при механических повреждениях в процессе первичной укладки трубы, а также при осадке, промерзании и оттаивании грунта.
Целью данной работы является разработка математической модели, алгоритма и программы для компьютерного моделирования и исследования электрических полей в системах КЗ трубопроводов с поврежденной изоляцией.
Математическая модель электрического поля
Пусть участок длины 2Lt горизонтального трубопровода защищен вертикальным глубинным анодом длины La, расположенным на расстоянии Lat от средней точки (x = 0) защищаемого участка трубы. Тогда потенциал u(p) постоянного электрического поля в области
,
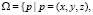
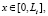
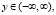
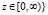удовлетворяет уравнению эллиптического типа [3, 5]:
; 
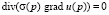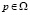, (1)
где σ(p) – удельная электропроводность среды, См/м.
К границам-изоляторам (Si) отнесем поверхность грунта (z = 0), вертикальные плоскости симметрии в грунте (x = 0 и x = Lt) и нижнюю границу анод-грунт (z = La), для которых потребуем выполнения краевых условий:
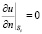, (2)
где n – вектор нормали к границе.
На границах «анод-грунт» (Sa) и «грунт-труба» (St) должны выполняться краевые условия третьего рода:
, 
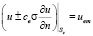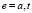, (3)
где u – потенциал в грунте, В; ca, ct – удельные сопротивления оболочки анода и изоляции трубы, Ом·м2; σ – электропроводность грунта, См/м; uam, utm – потенциалы металлов анода и трубы, В; здесь и далее индекс «a» относится к аноду, «t» – к трубе.
В граничных условиях (3) перед вторым слагаемым знак «+» соответствует условиям на аноде, знак «–» на трубе, так как направление электрического тока в системе принято положительным от анода в грунт, и от грунта к трубе.
Если зависимости плотности тока от разности потенциалов на границах Sa и St линейны, и при этом параметры анода и трубопровода не зависят от продольной координаты, то ca и ct – константы. Параметр ca зависит от координат точки на поверхности анода (ca = ca(z)), например, при моделировании составных анодов переменного радиуса, или при учете в модели процесса растворения оболочки анода. Параметр ct зависит от координат точки трубы (ct = ct (x)) при наличии неоднородностей изоляции, что является необходимым условием в задаче моделирования КЗ трубопровода с дефектами в изоляции.
Учитывая, что длины анода и трубы на несколько порядков превышают их диаметры, потенциалы металлов будем полагать постоянными в сечениях, т.е. зависящими только от продольной координаты: uam = uam(z), utm = utm(x).
Так как точка подключения анода к катодной станции находится в сечении z = 0, а точка подключения трубы – в сечении x = 0, то в качестве краевых условий в указанных сечениях примем:
; 
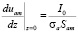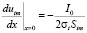, (4)
где σa, σt – удельные электропроводности металлов анода и трубы; Sam, Stm – площади их «металлических» сечений; I0 – ток катодной станции, А.
Полагая, что участок трубы, защищаемый одним анодом, симметричен относительно плоскости Y0Z, все расчеты проводятся для одной половины этого участка (0 ≤ x ≤ Lt), поэтому в знаменателе второй формулы (4) присутствует коэффициент «2».
Условием
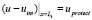(5)
обеспечивается необходимое значение защитного потенциала (uprotect) в точке трубопровода, наиболее удаленной от анода.
Алгоритм решения задачи (1)–(5) состоит из двух этапов. На первом этапе решается трехмерная задача, в которой отыскивается распределение потенциала и плотности тока вдоль трубопровода с учетом имеющихся отдельных дефектов в изоляции (участков с пониженным сопротивлением). На втором этапе алгоритма решается двумерная задача в нормальном сечении к трубопроводу на участке поврежденной изоляции, в которой моделируется электрическое поле с учетом углового расположения дефекта по окружности трубопровода.
Алгоритм решения трехмерной задачи
Для решения задачи (1)–(5) использован метод фиктивных источников, который применялся в расчетах электрических полей параллельных протяженных электродов без учета неоднородностей [8]. Аналогичный подход ранее применялся в [9].
Для перехода от непрерывной модели к дискретной представим глубинный анод в виде N конечных объемных элементов (КОЭ) длины La/N, а защищаемый участок трубопровода условно разобьем на M элементов длины Lt/M. Далее для каждого КОЭ будем оперировать средними значениями неизвестных параметров:
Uam, Utm – потенциал в металле КОЭ анода или трубы;
Uag, Utg – потенциал в грунте, граничащим с КОЭ;
Iaz, Itx – продольный ток в металле между соседними КОЭ;
Iag, Itg – ток, протекающий через боковую поверхность КОЭ.
При построении алгоритма каждый КОЭ анода (трубопровода) будем ассоциировать с фиктивным источником (стоком), расположенным в геометрическом центре КОЭ.
Применяя 1-й закон Кирхгофа к каждому КОЭ, с учетом (2), сформируем первый блок N+M уравнений:
, 
; 
, 
,
, 
; 
, 
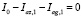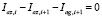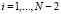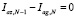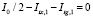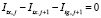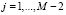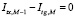. (6)
В соответствии с условиями (3) сформируем второй блок N+M уравнений:
; 
, 
; 
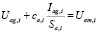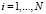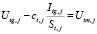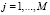, (7)
где Sa,i, St,j – площади боковых поверхностей КОЭ; ca,i, ct,j – сопротивления боковых поверхностей КОЭ.
Третий блок N+M–2 уравнений формируется из условия выполнения закона Ома:
; 
, 
; 
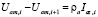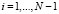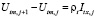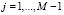, (8)
где ρa, ρt – продольные сопротивления сердечника анода и металла трубы между соседними фиктивными источниками, Ом.
Следующий блок N + M уравнений связывает потенциалы в грунте на границах КОЭ с интенсивностями точечных фиктивных источников (стоков):
; 
,
; 
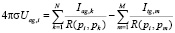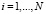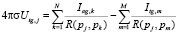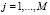, (9)
где R(pi, pk) – расстояние от точки pi, в которой определяется потенциал, до точки pk, в которой находится фиктивный источник (сток).
Применение формул (9) обосновано принципом электростатической аналогии [10] для пространственных задач распределения электрического поля. Для корректного применения соотношений (9) в алгоритме дополнительно используется метод зеркальных отражений [10], позволяющий перевести задачу из полупространства в пространство: при вычислении (9) суммируются слагаемые не только от реальных анода и трубы, но и от их зеркально-симметричных отражений относительно поверхности земли. Отметим, что последнее дополнение не увеличивает размерности итоговой системы уравнений.
Из условия (5) имеем последнее уравнение:
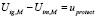. (10)
Таким образом, сформирована система линейных алгебраических уравнений (6)–(10), в которой число уравнений и неизвестных равно 4·(N+M).
Моделирование дефектных участков изоляции трубы
Определим несплошность изоляции трубопровода на КОЭ (ηiso) и коэффициент остаточного сопротивления дефектов (Kost):
; 
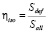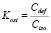, (11)
где Sdef – суммарная площадь дефектов в изоляции КОЭ; Sall = π·dt·Lt / M – площадь боковой поверхности КОЭ трубы; Siso = Sall − Sdef – площадь изоляции КОЭ без дефектов; Cdef – среднее удельное сопротивление дефектов; Ciso – удельное сопротивление изоляции.
Отметим, что безразмерный коэффициент (0 < Kost ≤ 1) при некоторых упрощающих предположениях можно трактовать как отношение средней толщины дефектной изоляции к толщине изоляции без дефектов.
Учитывая, что сопротивление изоляции без дефектов (Riso) и суммарное сопротивление дефектов на КОЭ (Rdef) определяются как
, 
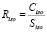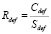, (12)
и, воспользовавшись соотношением для сопротивлений параллельных проводников [10], получим полное сопротивление боковой поверхности КОЭ:
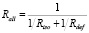. (14)
Численные результаты решения трехмерной задачи
Приведем пример расчета электрического поля КЗ трубопровода с тремя дефектами в изоляции, расположенными на различных расстояниях от точки подключения катодной станции. В таблице приведены значения основных параметров.
Значения основных параметров
|
Параметр |
Значение |
|
Длина защищаемого участка трубы (половина), км |
4 |
|
Внешний диаметр трубы, м |
1.22 |
|
Толщина стенки трубы, мм |
22 |
|
Уд. сопротивление стали, Ом·м |
2.45·10-7 |
|
Сопротивление неповрежденной изоляции трубы, Ом·м2 |
40000 |
|
Коэффициенты Kost для трех дефектов |
0.17; 0.16; 0.15 |
|
Расстояние между анодом и трубой, м |
200 |
|
Длина анода, м |
24 |
|
Диаметр стального сердечника анода, мм |
25 |
|
Внешний диаметр анода, мм |
120 |
|
Уд. сопротивление анодного композита, Ом·м |
0.01 |
На рис. 1 представлены функции распределения потенциала по границе трубопровод-грунт и в верхнем слое грунта параллельно оси трубы.
Из рисунков видно, что при минимальном защитном потенциале 0,3 В (значение потенциала в точке x = 4 км) на участках трубопровода с дефектной изоляцией значения защитного потенциала значительно ниже минимального, что является причиной усиленной коррозии.
Алгоритм и результаты численного решения двумерной задачи
Для решения задачи (1)–(5) в двумерном сечении, нормальном к оси трубопровода, применяется метод граничных элементов [2]. Для построения граничного интегрального уравнения воспользуемся интегральной формулой Грина, которая с учетом уравнения (1), для точек p и q, лежащих на границе S, примет вид:
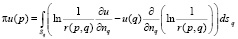, (15)
где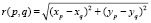 
– расстояние между точками p и q.
Из формулы (15) с учетом граничных условий (3), после некоторых преобразований будем иметь интегральное уравнение относительно неизвестной функции потенциала u(p)
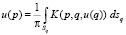, (16)
в котором ядро K(p, q, u(q)) определяется следующими соотношениями (аргументы p и q для краткости опущены):
; 
; 
,
; 
.
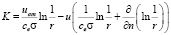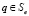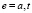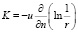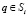Алгоритм решения построен на основе метода конечных сумм [2, 3] сведением граничного интегрального уравнения (16) к системе линейных алгебраических уравнений.
На рис. 2 представлены графики распределения потенциала по окружности трубы и в верхнем слое грунта по прямой, перпендикулярной оси трубопровода.
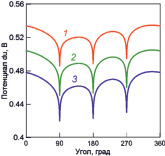
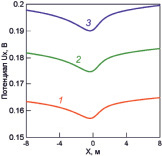
а) б)
Рис. 2. Распределения потенциала при угловых расположениях дефектов 90, 180 и 270 град; коэффициенте дефектности 0.001 и удельном сопротивлении грунта, равном, Ом·м: 1 – 500; 2 – 600; 3 – 700; (а) – грунт-труба; (б) – в верхнем слое грунта перпендикулярно оси трубопровода
Заключение
Предложена математическая модель и алгоритм расчета электрических полей в системах катодной защиты трубопроводов с повреждениями в изоляции. На основе метода фиктивных источников реализован алгоритм расчета электрического поля КЗ в трехмерной постановке. Уточнение углового расположения дефекта на окружности трубы осуществляется методом граничных элементов. Алгоритм программно реализован на языке C++ в кроссплатформенной интегрированной среде разработки приложений Code Blocks, распространяемой по лицензии GPL. Приведенные примеры расчетов служат иллюстрацией возможностей программы.