В последних два десятилетия внимание специалистов, изучающих тепловую сторону кристаллизации стальных слитков, занято созданием расчетных методов, позволяющих предсказать структуру слитка и в частности, конфигурацию усадочной раковины по его исходным параметрам – массе, размерам, температуре заливки металла в изложницу, химическому составу и т.д. В результате подобных исследований появилось большое количество статей, докладов, монографий [1–14]. Авторы подобных работ, решая проблему расчетными методами, часто получают результаты, более чем на порядок отличающиеся от фактических, что, конечно же, далеко от требуемого. По-прежнему, наиболее достоверными остаются экспериментальные результаты, однако задача теоретических направлений исследования с повестки дня не снимается. На наш взгляд несовпадение расчетных методов с экспериментальными по кинетике затвердевания, распределение температурных полей в слитке и т.д. происходит из-за приближенного или достаточно произвольного выбора граничных условий при решении уравнения теплопроводности из-за невозможности учета ряда сложнейших явлении, протекающих в системе слиток – изложница – окружающая среда. Нет никакого сомнения в том, что теоретически проблему кристаллизации слитка необходимо рассматривать с позиции и теплопроводности и массопереноса. При этом недопустимо исключить из рассмотрения следующие вопросы:
1) гравитационное перемещение жидкого металла в сердцевине слитка с учетом изменения его вязкостных характеристик вследствие изменения его состава и температуры;
2) конвективное перемещение металла в жидкой сердцевине по направлению противоположному гравитационному перемещению;
3) процессы массопереноса примесей при кристаллизации и связанные с ними ликвационные явления и изменения физических свойств расплавов;
4) физические и химические процессы, протекающие в двухфазной области и их влияние на процессы теплоотвода от слитка.
Разработанные в настоящее время математические модели учитывают слабо или не учитывают вообще выше перечисленные процессы, что и является основной причиной получения заведомо неточных результатов.
Наиболее точную информацию о протекающих сложных процессах при формировании стальных слитков дают экспериментальные методы исследования: изучение структуры слитков, измерение температурных полей в затвердевающем слитке и другие. Сочетание экспериментальных и расчетных методов является в настоящее время одним из оптимальных вариантов, позволяющих лучше объяснить наблюдающиеся закономерности кристаллизации стальных слитков.
Цель работы
Разработка математической модели формирования конфигурации усадочной раковине в слитке спокойной стали для прогнозирования уровня головной обрези и выхода годного.
Методика проведения исследований
В данной работе по имеющимся топографиям осевых темплетов 9 слитков спокойной стали строили уравнения кривой, описывающее конфигурацию усадочной раковины в слитке посредством решения системы дифференциальных уравнений. В плоском узком сечении слитка это линия пересечения фронта кристаллизации с одной стороны и уровня опускания жидкого металла в сердцевине слитка вследствие охлаждения и усадки с другой. Значения коэффициентов в итоговом уравнении находили подбором, варьируя значениями теплофизических параметров, отражающих условия теплопередачи от жидкого металла чугунной стенке и различных теплоизоляционных материалов. Признаком адекватности полученной математической модели являлось совпадение экспериментальной и расчетной формы раковины, когда сходимость соответственных значений не превышала + 5 %.
Затем по имеющимся уравнениям конфигурации усадочной раковины решалась обратная задача – определение тепловых потерь от головной части при различных режимах утепления. В качестве базовых вариантов были выбраны два способа утепления зеркала металла головной части асбеститом и отсевами алюминиевой стружки (ОАС) при утеплении внутренних боковых граней изложницы в верхней части теплоизоляционными плитами.
Самым существенным моментом в расчете конфигурации усадочной раковины является знание кинетики затвердевания металла в слитке. Затвердевание металла посредине широких граней бесконечной призмы прямоугольного сечения происходит почти так же, как и в бесконечной плите той же толщины. Затвердевание металла посредине граней призмы квадратного сечения приблизительно соответствует затвердеванию металла под слоем теплоизолирующей смеси и посредине широких граней изложницы и утеплителя в «листовом» слитке приближается к затвердеванию пластины.
Листовым считается слиток, в котором отношение широкой грани к узкой удовлетворяет условию: А2 /А1 ≥ 1,5. Для таких слитков затвердевание металла посредине узких граней и дна приближено заменяют затвердеванием цилиндрической отливки радиусом А1.
Построение математической модели и обсуждение результатов моделирования
Методика расчета конфигурации усадочной раковины предусматривает:
1. Расчет толщины слоя металла, затвердевшего за определенное время посредине одной из граней слитка или головной части (j = 1–6):
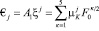(1)
где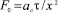 
– безмерное время; 
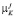– коэффициент, отражающий влияние теплофизическихпараметров материалов стенки, её толщины и формы слитка.
2. Расчет времени затвердевания расплава на любом горизонте Н слитка и h головной части:
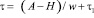и 
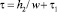(2)
где t1 – время, отсчитываемое с момента окончания наполнения слитка;
w – линейные скорости наполнения изложницы и головной части соответственно.
3. Расчет толщины Yj затвердевшего слоя металла от соответствующих граней слитка и головной части, измеренной горизонтальной плоскости:
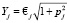(3)
где pj – тангенс угла наклона j – той грани к вертикали (j = 1,2,5,6,).
4. Приближенное сглаживание фронта вблизи границы раздела слиток-головная часть.
Для расчета сглаживания вводят величину dj и функции Z1 и Z2
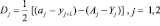(4)
где yj – значение на границе изложница – головная часть:
; 
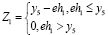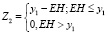(5)
Операцию сглаживания фронта выполняют по формулам:
Yj = Yj – dj(Z1/Y1)2
Yj+4 = Y j+4 + (Z1/Y)2, j =1,2 (6)
Здесь e и Е – вспомогательные эмпирические константы, определяющие степень взаимного влияния условий охлаждения металла в изложнице и утеплителе. Наиболее точное совпадение экспериментальной и расчетной формы раковины для различных слитков и при различных способах утепления получено при e ≈ 0,1 и Е ≈ 1.
5. Учет эффекта скругления углов.
Пусть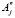 2
и 2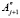
при j = 1,5 – размеры поперечного сечения слитка или головной части на некотором горизонте. Тогда максимальные размеры поперечного сечения жидкого расплава на том же горизонте в момент времени t будут 2(
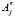– Yj) и 2(
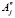– Yj+1).
Площадь S(h) (h = h или h = Н) жидкого металла на соответствующем горизонте
S(h) = [С –(c – p)Yj /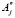
] (
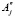– Yj) (
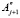– Yj+1), j = 1,5 (7)
где: константа С задается равной 4 для прямоугольного и 3,14 для j эллиптического (или круглого) сечения.
6. Усадка металла при образовании поверхностной корочки – слоя металла, затвердевшего в изложнице и головной части при их наполнении, полостью компенсируется вновь поступающими порциями расплава. Поэтому при расчете усадочной раковины принимают во внимание только объем жидкого металла в изложнице и головной части (V0h и V0П) к моменту окончания наполнения.
7. Изменение объема расплава в головной части обусловлено как его затвердеванием, так и расходом на компенсацию усадки металла, затвердевшего к данному моменту времени в изложнице и в самом утеплители. Объем металла Vn, затвердевшего за время t > 0 в головной части после ее наполнения:
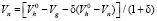(8)
8. Вывод уравнения движения зеркала металла в головной части основан на балансе металла в процессе затвердевания слитка. При выводе принимают, что движение расплава в головной части обусловлено уменьшением объема стали при переходе ее из жидкого состояния в твердое и соответствующим потоком жидкости из головной части в тело слитка. При принятых обозначениях скорость опускания мениска жидкого металла в утеплителе составит [(dh1)/ (dτ)], а объемный расход металла из утеплителя S(h1) [(dh1)/(dτ)].
Снижение уровня расплава в утеплителе происходит за счет: питания металла, затвердевшего в изложнице:
(dVh)/(dτ)=δ{[d(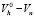
)]/dτ};
компенсации усадки металла, затвердевшего в утеплителе:
δ[(dVh)/dτ);
толщения моста Y4 на мениске:
S(h1){[d Y4(τ)/(dτ)}
Итак, расход жидкого металла из головной части при h1 > 0 определяется уравнением:
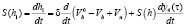(9)
а при h1 < 0,т.е. при проникновении усадочной раковины в тело слитка, – уравнением:
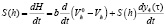(10)
Уравнения (9) и (10) представляют собой требования баланса расхода металла и являются ключевыми при расчете конфигурации усадочной раковины. В качестве граничного условия можно принимать либо уровень металла в головной части в начальный момент процесса:
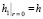(11)
либо уровень металла в головной части в момент окончания затвердевания слитка:
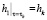(12)
По физическому смыслу граничное условие (11) соответствует заданному объему металла в головной части, для которого расчетом определяют форму усадочной раковины и положение ее дна. Граничное условие (12) соответствует положению дна усадочной раковины, которая определяется требуемым запасом металла в головной части. В этом случае расчетом определяют высоту налива металла в головной части, а, следовательно, и ее первоначальный объем, обеспечивающий заданную глубину усадочной раковины.
Объем жидкого металла в изложнице для любого момента времени определяем по формуле:
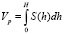(13)
объем жидкого металла в головной части:
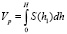(14)
Решая уравнение (9) относительно (dh1)/(dτ), получим изменение во времени уровня жидкого металла в утеплителе h1 а также положение и количество жидкой фазы к концу затвердевания тела слитка.
Конфигурация самой усадочной раковины в слитке существенно зависит от поведения твердого металла «моста», образующегося при затвердевании стали сверху. В расчете принимают, что корочка затвердевшего сверху металла (мост) пластична. При опускании расплава и сужении площади жидкого металла под мостом материал на краях равномерно «размазывается» по корочке, намерзшей на боковых гранях утеплителя, увеличивая ее толщину.
Пусть r1 и r – координаты границ видимой усадочной раковины вдоль осей симметрии на уровне h = h1 + Y4 = h2. За время dτ уровень металла в головной части опускается на величину dh; на столько же опустится мост затвердевшего сверху металла. Если при этом сечение утеплителя сужается, то в новом положении края моста окажутся избыточными. Произойдет «намазывание» избыточного объема металла на твердую корочку, застывшую от боковых стенок головной части.
Рассчитываем время приращения этого избыточного объема на узкой (j = 1) и широкой (i = 2) сторонах утеплителя:
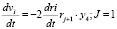(15)
В то же время это приращение избыточного объема может быть определено по толщине намазанного слоя bj (j = 1,2 по узкой и широкой стороне утеплителя соответственно):
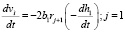
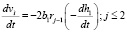(16)
Из уравнений (15) и (16) определяем толщину b с двух сторон слоя: bj= y4[(drj)/(dh)] j = 1,2. Обозначим (drj)/(dh)=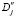 
Dj =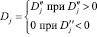 
Тогда координаты видимой усадочной раковины можно рассчитать по формуле:
rj+2 = rj + y4(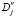
) (17)
Если при опускания мениска размеры его не уменьшаются (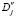
≤ 0,) то размазы-вание моста происходить не будет (rj+2 = r).
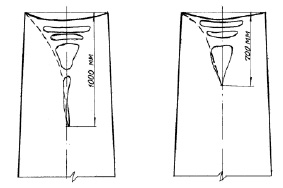
а) б)
Сопоставление расчетной (------) и фактических данных ( —— ) по форме усадочной раковине слитков, утепленных асбеститом (а) и отсевами алюминиевой стружки (б)
Таким образом, наряды с координатами зеркала расплава, опускающегося по мере затвердевания слитка, получаем координаты видимой усадочной раковины.
Расчет кинетики затвердевания слитков с различным режимом утепления головной части осуществляли по программе, составленной по уравнениям (1–17). Результаты расчета конфигурации усадочной раковины сопоставляли с конфигурацией реальных усадочных раковин слитков, отлитых в изложницы 16Н и 21Н, показаны на рисунке. Оба слитка отлиты в уширенные книзу изложницы с теплоизоляционными плитами, утепленными соответственно асбеститом и отсевами алюминиевой стружки (ОАС).
Размеры изложницы16Н принимались 1177х764 мм, 21Н-1574х764 мм, высота налива металла в обеих изложницах 2400 мм. Температура металла по окончании наполнения изложницы для всех вариантов принималась 1525 °С. Толщина теплоизоляционных плит – 40 мм, глубина погружения в металл 400 мм, толщина слоя наружного утеплителя 100, конусность изложницы 2 %.
Подбор коэффициентов в результирующем уравнении прекращался, когда различие в расчетных и фактических значениях по горизонтальной координате не превышал 5 %. Обращает на себя внимание, что касательная к продвижению фронта кристаллизации на начальном этапе затвердевания наклонена к горизонтали (вершинами) под углом 45°. Это свидетельствует о примерном равенстве скоростей кристаллизации от стенки изложницы и от теплоизоляционной засыпки. Действительно, после образования газового зазора между изложницей и слитком теплоотвод от слитка резко сокращается и становится примерно равным потерям через зеркало металла и теплоизоляционную засыпку.