Под сетями Чебышева подразумеваются сети с равносторонними ячейками. Их удобно использовать при проектировании геометрии раскроя тентовых оболочек, в связи с аналогией поведения тентовых материалов в процессе формообразования криволинейных поверхностей. Теоретические аспекты и вопросы практического расчета наложения сетей Чебышева на сложные поверхности рассмотрены авторами в ряде работ [1–2, 4]. В настоящей статье описывается способ практического расчета изменения углов между нитями сети при наложении ее на криволинейную поверхность. Учитывая, что реальные тентовые материалы имеют ограничения в трансформации сетевых углов, необходимы расчет и определение на поверхности оболочки зон возможного применения материалов – допустимых границ раскроя.
Рассмотрим участок сети Чебышева на криволинейной поверхности (рис. 1). Линии сети являются системой криволинейных координат u,v на поверхности.
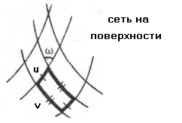
Рис. 1. Участок сети Чебышева
Известно [3], что длина линейного элемента в такой координатной сети определяется соотношением (1), предложенным Чебышёвым:
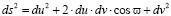 (1)
(1)
Здесь: ώ – сетевой угол,
ds – длина линейного элемента на поверхности между узлами i + 1, j и i, j + 1.
Сетевой угол – это угол между координатными линиями сети на поверхности.
В работе [4] показано, что при малых значениях размеров сторон сети по сравнению с радиусами кривизны поверхности, для практических задач расчета и проектирования оболочек строительного назначения, допустима замена криволинейных дуг прямолинейными хордами, стягивающими эти дуги. Схематически такая замена показана на рис. 2.
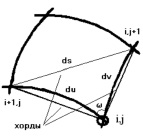
Рис. 2. Схема замены дуг сети хордами
Такая замена позволяет значительно упростить алгоритм вычисления значений искомых сетевых углов при известных декартовых координатах узлов сети. Алгоритм расчета в этом случае имеет вид:
1. обозначив в декартовой системе, значения координат смежных узлов ячейки сети через:
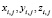 ;
; 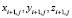 ;
;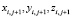 ,
,
вычислить приращения координат узлов:
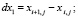
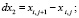
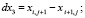
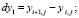
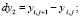
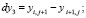
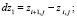
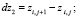
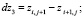
2. вычислить квадраты длин дуг, как квадраты длин хорд:
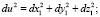
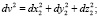
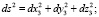
3. вычислить искомый сетевой угол по формуле (2), выведенной из уравнения (1):
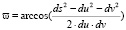 (2)
(2)
Этот алгоритм был реализован в разработанной авторами программе исследования возможностей наложения сетей Чебышева на некоторые поверхности отрицательной кривизны (рис. 3). Программа содержит модуль «сетевые углы» для вычислений по приведенному алгоритму и блок «границы», который позволяет графически отображать результаты расчета в виде точечного выделения областей сети, в которых изменение сетевого угла не превышает задаваемого предела.
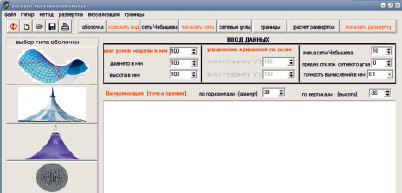
Рис. 3. Общий вид главного окна программы, разработанной авторами для исследования и проектирования тентовых оболочек
На рис. 4 и 5 приводится графическое представление результатов решения такой задачи на примере компьютерного проектирования тентовых оболочек разной геометрии.
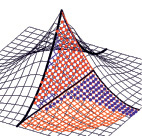
Рис. 4. Узлы сети Чебышева с допустимыми значениями сетевых углов на параболическом шатре (показаны узлы на ¼ поверхности)
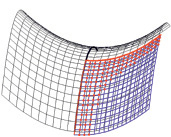
Рис. 5. Узлы сети Чебышева с допустимыми значениями сетевых углов на гиперболическом параболоиде (показаны узлы на ¼ поверхности)
Таким образом, получены формулы, а также разработаны алгоритм и компьютерная программа, показывающие возможность автоматизированного расчета допустимых границ наложения плоских пленочно-тканевых заготовок на криволинейные поверхности тентовых покрытий строительных сооружений по предлагаемой выше методике.

