Ведущиеся в последние годы активные исследования различных искусственных магнитодиэлектрических структур – электромагнитных кристаллов (ЭК), связаны с появившимися технологическими возможностями их изготовления и применения в микроволновом и оптическом диапазонах. Основное свойство, привлекающее внимание исследователей и обуславливающее возможность разнообразных практических приложений ЭК, – существование запрещенных зон в спектре собственных электромагнитных состояний таких объектов, т.е. частотных диапазонов, в пределах которых полностью подавляется распространение излучения через кристалл. Конструктивно, как правило, подобные структуры представляют собой решетки диэлектрических либо металлических элементов, периодически распределенных в пространстве. При этом регулярность расположения, наряду с формой элементов, является фактором, определяющим особые электродинамические свойства таких материалов [2].
Следует, однако, отметить, что в настоящее время не существует принципиальной возможности создания абсолютно регулярных наноразмерных объектов. В свою очередь любые нарушения внутренней структуры ЭК должны вызывать изменение его характеристик. Настоящая работа посвящена изучению влияния неупорядоченности ЭК на их электродинамические характеристики.
Методика численного моделирования и обсуждение результатов
Рассмотрим сказанное на примере двумерного ЭК, состоящего из тонких металлических проводников, ориентированных параллельно друг другу. Такая структура обладает полосой непропускания излучения – запрещенной зоной – в области низких частот. Предполагалось, что ЭК возбуждается плоской волной. Размеры кристалла – 11 рядов элементов вдоль направления прихода излучения и 21 ряд поперек.
Методика расчета поля в таких ЭК основывалась на методе разделения переменных, не налагающем ограничений на взаимное положение цилиндров и источника поля. При этом поле в структуре представлялось в виде суммы известного первичного поля и неизвестного вторичного поля, рассеянного на элементах. Последнее записывалось в виде бесконечных рядов по элементарным волновым функциям с неизвестными коэффициентами. В частности, поле, рассеянное на N элементах, искалось в виде суммы N дифракционных рядов, в которой один из рядов составлен из волновых функций одного тела, а волновые функции в остальных рядах при помощи теорем сложения выражены через собственные волновые функции первого тела. Далее из удовлетворения граничным условиям на поверхности каждого цилиндра получались бесконечные системы уравнений с бесконечным числом неизвестных – искомых коэффициентов разложения. Данные уравнения разрешались при усечении рядов на основе допущения о малости геометрических размеров элементов структуры [3].
На рис. 1 сплошной линией представлена рассчитанная таким образом частотная зависимость коэффициента прохождения волн через ЭК, полученная для Е – поляризации (вектор напряженности электрического поля ориентирован параллельно осям элементов) в предположении, что период расположения элементов d составляет 1,4 см, радиус – 0,05 см. Штриховая линия описывает спектр пропускания аналогичной структуры, но с нарушенной упорядоченностью за счет случайного смещения элементов в интервале значений [-d/5, d/5] относительно исходных в регулярной структуре. Следовательно, рассматривается случай весьма малой неупорядоченности. Здесь и далее данные усреднены по 600 структурным реализациям.
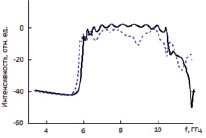
Рис. 1. Спектры пропускания регулярного и слабо неупорядоченного ЭК
Сравнение представленных кривых демонстрирует крайне незначительное изменение спектральной картины прошедшего через структуру излучения при малых нарушениях в периодичности размещения элементов. Важно, что при этом положения запрещенной и разрешенной зон на частотной оси практически не меняются.
Рассмотрим данную ситуацию, анализируя пространственное распределение поля внутри ЭК. Известно [1], что для подобных структур характерна возможность локализации излучения во внутренних областях, особенно ярко проявляющаяся на частотах, близких к границе запрещенной и разрешенной зон. Это позволяет говорить о наличии у металлических ЭК ярко выраженных резонансных свойств.
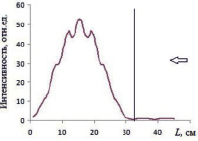
Рис. 2. Пространственное распределение излучения в регулярном ЭК
На рис. 2 представлено пространственное распределение интенсивности поля вдоль упорядоченного ЭК, полученное на частоте 6,1 ГГц. Вертикальной линией на рисунке обозначена облучаемая граница структуры, стрелкой – направление прихода излучения. Наблюдается значительная концентрация энергии в центральной области кристалла, связанная с формированием в структуре стоячей волны, что позволяет использовать его в качестве своеобразного объемного резонатора, способного функционировать в широком диапазоне частот.
На рис. 3 изображено подобное распределение в структуре с нарушениями регулярности. Кривая 1 здесь описывает полную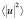 
, кривая 2 – когерентную 
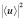интенсивности излучения, где u – амплитуда поля в отдельной реализации.
Известно, что полная интенсивность, имеющая смысл плотности энергии поля, может быть представлена в виде суммы двух составляющих: когерентной и флуктуационной (диффузионной). Когерентная часть определяется степенью фазовой согласованности суммарных рассеянных полей во всех реализациях размещения элементов, т.е. характеризует наличие какой-либо регулярности в расположении элементов кристалла.
Из рис. 3 очевидно резкое уменьшение степени локализации излучения, хотя формы кривых полной и когерентной интенсивностей еще сохраняют взаимное подобие с максимумом в центральной области ЭК.
Сравнение с абсолютными значениями интенсивности поля, представленными на рис. 2, указывает на практическую невозможность использовать подобную структуру в качестве резонаторной системы. Здесь же следует отметить повышение уровня излучения, отраженного от структуры, что свидетельствует об увеличении ее рассогласованности с окружающим пространством.
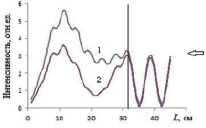
Рис. 3. Пространственное распределение излучения в неупорядоченном ЭК (1 – полная, 2 – когерентная интенсивности)
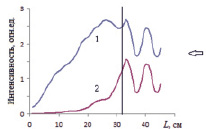
Рис. 4. Пространственное распределение интенсивности поля в абсолютно неупорядоченной структуре. Обозначения кривых – аналогично рис. 3
Интересным представляется рассмотрение свойств аналогичного объекта на тех же частотах, но уже в случае абсолютной неупорядоченности в расположении элементов. Со структурами, описанными выше, такую систему объединяет только средняя плотность компоновки элементов на той же площади. На рис. 4 представлены результаты расчета поля в такой структуре, из которых, во-первых, следует исчезновение когерентной составляющей излучения при прохождении поля через случайную структуру, что физически достаточно очевидно. Во-вторых, видно, что энергия локализуется вблизи облучаемой границы системы цилиндров, что позволяет считать неупорядоченную дискретную среду своеобразным экраном, отражающим электромагнитное излучение.
Заключение
Таким образом, на примере металлических ЭК показано, что привнесение даже малых неупорядоченностей во внутреннюю структуру таких материалов может приводить к существенному изменению их электродинамических свойств. Увеличение же степени неупорядоченности приводит к абсолютному изменению их характеристик, в частности, коэффициентов отражения и похождения, а также пространственного распределения поля внутри кристаллов.
Работа поддержана грантом РФФИ № 12-02-98010.