Напряженное состояние волнового нагруженного тела может изменяться так быстро, что возникающие деформации и разрушения еще не успевают распространиться. После трехкратного или четырехкратного прохождения и отражения волн напряжений в теле процесс распространения возмущений становится установившимся, напряжения и деформации усредняются, тело находится в колебательном движении.
В работе [1] приводится следующая информация: «Если здание расположено близко к центру взрыва, то взрывная волна может его разрушить. С другой стороны, если здание находится на достаточном расстоянии, то оно может испытать лишь сотрясение. Когда атомная бомба была взорвана над Японией в конце второй мировой войны, это чудовищное оружие разрушило большое число сооружений, но – удивительное исключение – многие высокие трубы оказались неповрежденными. На фото XXIX показан город Нагасаки, снятый с точки, над которой разорвалась бомба (около полутора километров в стороне от центра группы заводских труб). На фото видны несколько труб, которые выстояли, несмотря на общее опустошение
вокруг них».
На рис. 1 [10] показан город Нагасаки, снятый с расстояния около полутора километров в сторону от центра группы заводских труб, над которой разорвалась бомба. Видны несколько труб, которые выстояли (рис. 1).
Рассмотрим задачу о взрывном воздействии на сооружение (дымовая труба), которое находится в грунтовой и воздушной средах.
Рис. 1. Город Нагасаки после взрыва атомной бомбы в 1945 году
В работах [2–9] приведена информация о применении численного моделирования нестационарных волн напряжений в областях сложной формы.
Постановка задачи
Рассматриваемые физические процессы решаются с помощью методов математического моделирования. Рассмотрим некоторое тело, состоящее из двух разных областей Г(1) (воздушная среда) и Г(2) (грунтовая среда) (рис. 2) в прямоугольной декартовой системе координат XOY, которому в начальный момент времени t = 0 сообщается механическое
воздействие.
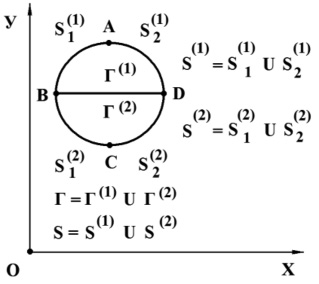
Рис. 2. Некоторое тело, состоящее из двух разных областей Г(1) и Г(2) в прямоугольной декартовой системе координат XOY
Предположим, что тело Г(1) изготовлено из деформируемой воздушной среды и является однородным изотропным материалом, подчиняющегося упругому закону Гука при малых упругих деформациях. Если в деформируемом твердом теле предположим, что поперечная скорость распространения равна нулю, то можно получить уравнения состояния для воздушной среды.
Точные уравнения двумерной плоской динамической теории упругости для области Г(1) имеют вид
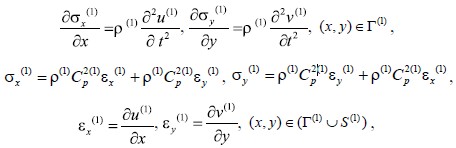(1)
где: σx(1) и σy(1) – компоненты тензора упругих напряжений; εx (1) и ε y(1) – компоненты тензора упругих деформаций; u(1) и v(1) – составляющие вектора упругих перемещений вдоль осей OX и OY соответственно; ρ(1) – плотность материала; Cp(1) – скорость продольной упругой волны; 
– граничный контур тела Г(1).
Систему (1) в области, занимаемой телом Г(1), следует интегрировать при начальных и граничных условиях.
Точные уравнения двумерной плоской динамической теории упругости для области Г(2) имеют вид
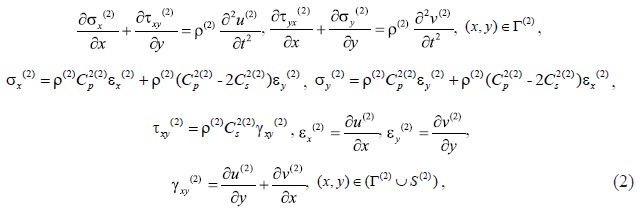
где: σx(2), σy(2) и τxy(2) – компоненты тензора упругих напряжений; εx(2), εy(2) и γxy(2) – компоненты тензора упругих деформаций; u(2) и v(2) – составляющие вектора упругих перемещений вдоль осей OX и OY соответственно; ρ(2) – плотность материала; Cp(2) – скорость продольной упругой волны; 
– скорость поперечной упругой волны; 
– граничный
контур тела Г(2).
Систему (2) в области, занимаемой телом Г(2), следует интегрировать при начальных и граничных условиях. Для решения краевой задачи используется метод конечных элементов в перемещениях.
Решение задачи о сосредоточенном упругом взрывном воздействии
Рассмотрим задачу о сосредоточенном упругом взрывном воздействии на границе воздушной и грунтовой сред (рис. 3–5).
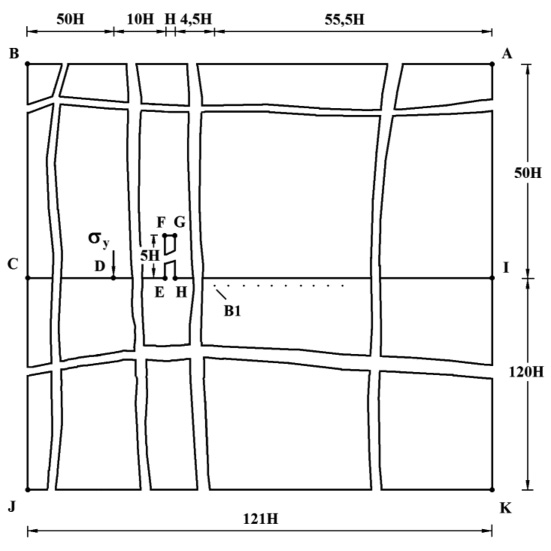
Рис. 3. Постановка задачи для сооружения (дымовая труба) при соотношении ширины к высоте один к пяти
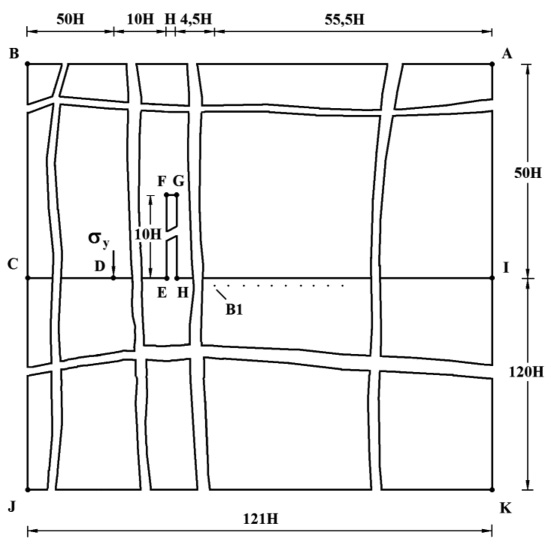
Рис. 4. Постановка задачи для сооружения (дымовая труба) при соотношении ширины к высоте один к десяти
В работе рассмотрены три варианта сооружения (дымовых труб): соотношение ширины к высоте один к пяти (рис. 3); соотношение ширины к высоте один к десяти (рис. 4); соотношение ширины к высоте один к пятнадцати (рис. 5).
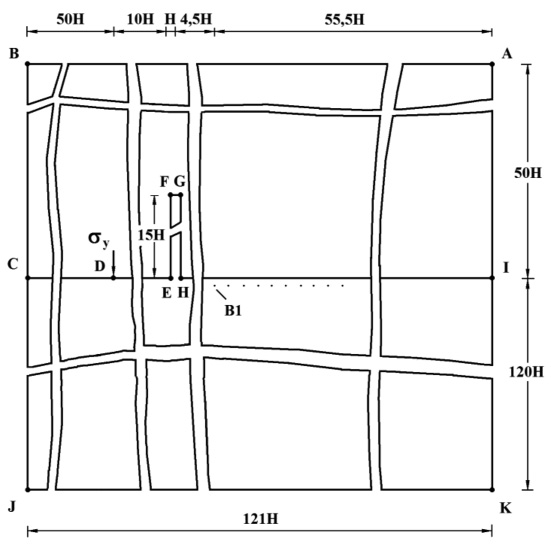
Рис. 5. Постановка задачи для сооружения (дымовая труба) при соотношении ширины к высоте один к пятнадцати
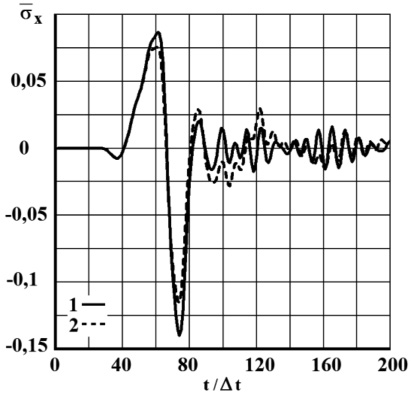
Рис. 6. Изменение упругого нормального напряжения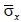 
во времени t/∆t в точке B1: 1 – в задаче без сооружения; 2 – в задаче с сооружением (дымовая труба) при соотношении ширины к высоте один к пяти
В точке D перпендикулярно поверхности грунтовой среды IHEDC приложено нормальное напряжение σy, которое при 0 ≤ n ≤ 10 (n = t/∆t) изменяется линейно от 0 до P, а при 10 ≤ n ≤ 20 изменяется от P до 0 (P = σ0, σ0 = – 0,1 МПа (– 1 кгс/см2)). Граничные условия для контура ABCJKI при t > 0 
.
Отраженные волны от контура ABCJKI не доходят до исследуемых точек при 0 ≤ n ≤ 200. На границе IHGFEDC приняты условия непрерывности перемещений.
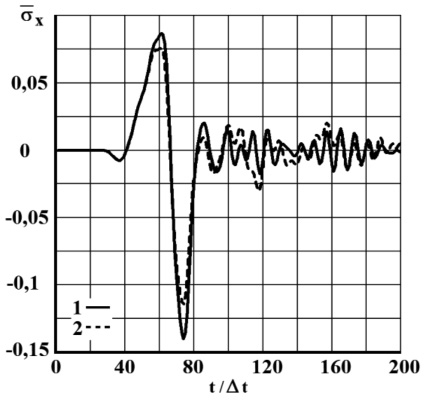
Рис. 7. Изменение упругого нормального напряжения 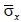во времени t/∆t в точке B1: 1 – в задаче без сооружения; 2 – в задаче с сооружением (дымовая труба) при соотношении ширины к высоте один к десяти
Для области ABCDEFGHI приняты следующие исходные данные: H = ∆x = ∆y; ∆t = 0,147×10-4 с; ρ = 1,22 кг/м3 (1,22×10-9 кгс с2/см4); Cp = 340 м/с. Для области IHGFEDCJK приняты следующие исходные данные: H = ∆x = ∆y; ∆t = 0,125×10-4 с; ρ = 1,469×103 кг/м3 (1,469×10-6 кгс с2/см4); Cp = 400 м/с; Cs = 250 м/с. В расчетах принимается минимальный шаг по времени, то есть ∆t = 0,125×10-4 с. Исследуемая расчетная область имеет 20862 узловых точек. Решается система уравнений из 83448 неизвестных. На рис. 6–8 показано изменение упругого нормального напряжения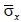 
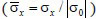во времени n в точках B1, находящихся около свободной поверхности упругой полуплоскости.
Полученные результаты показывают, что дымовые трубы уменьшают нормальные напряжения на границе сред в окрестности сооружения.
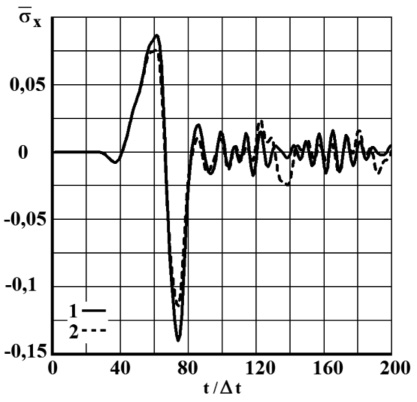
Рис. 8. Изменение упругого нормального напряжения 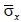во времени t/∆t в точке B1: 1 – в задаче без сооружения; 2 – в задаче с сооружением (дымовая труба) при соотношении ширины к высоте один к пятнадцати