Обозначаемая нормативными образовательными документами практико-ориентированная направленность подготовки бакалавров, безусловно, отвечает требованиям современного рынка труда. Однако, проводимое на этой образовательной доктрине резкое секвестирование рабочих программ по математике обозначило проблему резкого снижения качества фундаментальной подготовки, особенно в системе гуманитарного образования образования. Математическое образование следует рассматривать как важнейшую составляющую фундаментальной подготовки бакалавра любого профиля. Современный специалист работает в условиях математизации и информатизации профессиональной сферы, когда при решении прикладных задач не обойтись без информационных технологий, связанных с использованием персонального компьютера и компьютерных сетей. В то же время математика является не только мощным средством решения прикладных задач, но и элементом общей культуры. Изучение математики интеллектуально обогащает студента, развивая гибкость и строгость мышления, необходимые для будущего бакалавра. Чтобы грамотно поставить прикладную задачу и подготовить ее к решению на компьютере, необходимо знать основы математического и компьютерного моделирования, а это в свою очередь требует знания основ теории множеств, математической логики и других разделов математической науки.
Таким образом, практико-ориентированная математическая компетентность бакалавра предполагает овладение фундаментальными математическими методами на уровне, достаточном для успешного решения социально-ориентированных, профессионально-направленных задач в соответствующей сфере деятельности.
Анализ характера математизации различных областей профессиональной деятельности позволяет условно разделить все существующие направления подготовки высшего профессионального образования на три группы. К первой группе можно отнести специальности, для которых математические знания и умения составляют существо будущей профессиональной деятельности – «математико-ориентированные» направления подготовки. Ко второй группе отнесем «математико-профильные» направления подготовки, в которых уже разработаны и используются математические модели, а одной из целей преподавания математики является подготовка студентов к изучению таких моделей и выработка навыков их использования. Третью группу составляют направления подготовки «латентно-профильные» по отношению к математике, для которых основной целью преподавания дисциплины, является интеллектуальное развитие личности средствами математики. Однако, учитывая тот факт, что стремительное развитие прикладной математики и информатики приводит к постепенному переходу все новых направлений подготовки из третьей группы во вторую, целесообразно их объединить в одну группу, условно названную нематематическое направление подготовки. Именно для этого класса направлений подготовки особенно актуально стоит задача разработки таких подходов к проектированию содержания дисциплины «Математика», которые обеспечивали бы единство и взаимосвязь фундаментальной и прикладной компонент математического знания.
В данной статье представлены концептуальные основы и результаты внедрения в образовательную практику такого дуального подхода к проектированию системы математического образования для бакалавров нематематических специальностей.
Методология предлагаемого подхода. При определении концептуальных основ совершенствования системы математической подготовки была сформулирована система принципов, условно названных «проектировочными»:
• принцип информационной целостности учебного содержания, обеспечивающий сохранение логической структуры предметной области «Математика»;
• принцип социальной эффективности, предполагающий научную обоснованность отбора профессионально-значимого содержания предметной области «Математика»;
• принцип единства фундаментальной и профессионально- ориентированной компонент учебного содержания при построении рабочих программ курса «Математика»;
• принцип взаимосвязи содержательной и процессуальной сторон образовательного процесса при организации системы предметной подготовки по дисциплине.
Последовательное соблюдение этих принципов позволило предложить и реализовать процедурную схему реализации предлагаемого подхода, состоящую из четырех этапов:
1. Построение модели предметной области «Математика».
2. Проведение профессиографической экспертизы специалистов с целью определения математического знания, необходимого для успешного освоения соответствующей профессиональной деятельности.
3. Построение модели соответствующей ННП в виде подмодели предметной области «Математика».
4. Определение макета рабочей программы для всего множества ННП и формирование рабочей программы конкретной ННП.
Первый этап. Для построения модели предметной области «Математика» использовался аппарат теории графов [1]. Для наглядного отображения взаимосвязей между отдельными элементами предметной области структура ее модели была представлена в виде размеченного графа с тремя типами вершин и тремя типами дуг. К первому типу относятся вершины, представляющие разделы и подразделы математики, определяющие логику построения дисциплины; ко второму – классы задач, определяющие умения, которые необходимо получить студентам на практических занятиях; к третьему – математические пакеты прикладных программ (МППП), с помощью которых студенты могут решать более сложные задачи. Связи между этими вершинами изображаются с помощью следующих типов дуг структурная связь, логическая связь, вычислительная связь.
На основании анализа федеральных государственных образовательных стандартов было выделено семь разделов математики, обязательных для изучения в том или ином объеме на всех специальностях. Структурирование учебного материала каждого раздела и установление взаимосвязей между их учебными элементами, позволило представить схемы каждого подраздела в виде соответствующих подграфов, в которых представлено содержание всех типов вершин и установлены соответствующие типы связей между ними. Процесс структурирования в каждом разделе заканчивался нахождением учебного элемента, который представляет собой наименьшую, самостоятельную дидактическую единицу, т.е. дальше не структурируется. На рис.1 в качестве примера представлена часть общего графа модели –
раздел.
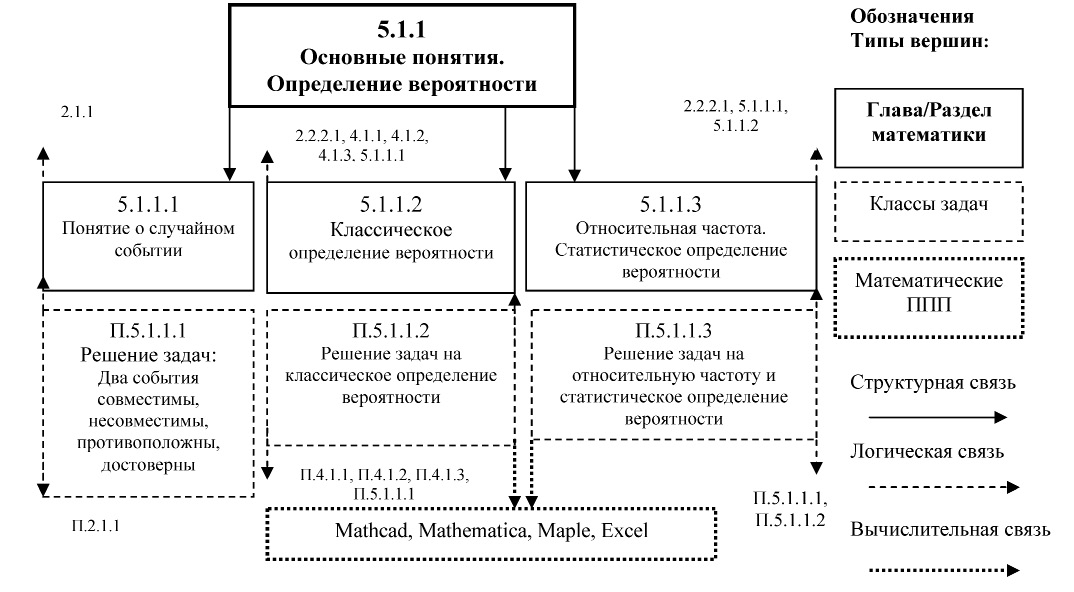
Рис. 1. Модель математики. Схема раздела 5.1.1
5.1.1. «Основные понятия. Определение вероятности» [2,3].
Второй этап. Для определения концептуального ядра математического знания, необходимого для успешного осуществления профессиональной деятельности по соответствующей специальности, была разработана процедура анкетирования экспертов и методика обработки экспертных оценок [4]. В качестве экспертов выступали преподаватели вузов и специалисты соответствующих профессиональных областей, условно разделенные на две группы – преподаватели и работодатели. Обработка экспертных оценок состояла из двух этапов.
1. Фиксирование уровня компетентности экспертов. Степень компетентности экспертов в области математики определялась на основе их ответов на вопросы о частоте использования математических знаний и пакетов прикладных программ в их работе. Было принято, что эксперты, постоянно использующие математические знания в своей работе, имеют степень компетентности, равную 1, использующие их иногда – степень компетентности, равную 0,6, не использующие их – 0,3. Суммарная компетентность экспертов рассчитывается по формуле:
![]() , (1)
, (1)
где n2, n3 – количество экспертов с соответствующими степенями компетентности.
2. Определение коэффициента важности элементов модели. Для согласования мнений разных экспертов, выбравших один и тот же ответ на некоторый вопрос, использовалась следующая формула:
![]() , (2)
, (2)
где ![]() – количество экспертов, которые положительно ответили на данный вопрос анкеты с соответствующей степенью компетентности.
– количество экспертов, которые положительно ответили на данный вопрос анкеты с соответствующей степенью компетентности.
Третий этап. Проведенное анкетирование специалистов позволило определить коэффициенты важности каждой вершины соответствующего типа в общей модели предметной области «Математика» и построить, тем самым, профессионально-ориентированные модели математики. Каждой вершине графа приписывается ее «вес», соответствующий вычисленным коэффициентам важности данных элементов модели. Отдельно проставляются коэффициенты важности теоретической части раздела – математических понятий и практической части – соответствующих классов задач.
Четвертый этап. Информация, полученная от экспертов-профессионалов, интерпретируется экспертами-математиками – формируется модель программы курса «Математика» для конкретной специальности в виде соответствующих подграфов общего графа модели предметной области. Вершины типа «раздел математики» в модели программы курса «Математика» определяют структуру программы этого курса и содержание его теоретической части, вершины типа «класс задач» – содержание практической части курса. Вершины типа «математические пакеты прикладных программ» определяют рекомендации по использованию математических пакетов прикладных программ для поддержки этого курса. Рассчитанные коэффициенты важности этих вершин определяют рекомендации по степени детализации изучения соответствующих разделов курса. Для возможности однозначной интерпретации получаемых значений при отображении учебной информации соответствующих разделов в рабочих программах по математике, была разработана шкала соответствия коэффициентов важности уровням представления и усвоения учебной информации [5].
Важным этапом построения любой рабочей программы является тематическое планирование курса, предполагающее распределение учебного времени на различные формы аудиторных занятий. Введение коэффициентов важности каждого учебного элемента потребовало перераспределения часов, отводимых на изучение каждого раздела дисциплины (его теоретической и практической частей). В результате всех проведенных мероприятий была предложена новая форма рабочей программы курса «Математика», универсальная для всех нематематических специальностей, по которым ведется обучение в классическом университете. В программах, помимо учебного содержания, приводятся подробные рекомендации по уровню изучения каждого учебного элемента, возможным классам задач, которые можно использовать для закрепления теоретического материала, предлагаются пакеты прикладных программ, использование которых способствует закреплению основных математических знаний и умений.
Основные результаты педагогического эксперимента. Эффективность предлагаемого подхода проверялась в ходе педагогического эксперимента, проведенного на трех нематематических специальностях Дальневосточного федерального университета – «География», «Управление персоналом» и «Социально-культурный сервис и туризм».
1. Внутрипредметный этап эксперимента. Для обеспечения принципа взаимосвязи содержательной и процессуальной сторон образовательного процесса была предложена система рейтингового оценивания знаний студентов. Предварительно, для унификации процедуры сравнения и анализа показателей различных видов учебной деятельности, была разработана единая схема предметной подготовки по курсу «Математика», определены виды контролирующих мероприятий, по каждому из которых разработаны оценочные шкалы. Для каждого вида отчетности было разработано соответствующее дидактическое обеспечение. В результате такой организации учебного процесса к концу семестра по каждому разделу/подразделу курса у студентов имелась определённая совокупность оценок, которые суммировались в интегральный показатель успеваемости.
На всех специальностях значение показателя в экспериментальных группах практически по всем разделам хоть незначительно, но превышает соответствующие значения в контрольных. Полученные положительные результаты можно связать с верным подходом к построению модели предметной области и методики отбора профессионально-значимого математического содержания, которые послужили основанием для формирования логической основы рабочей программы.
2.Межпредметный этап эксперимента. На этом этапе проверялось предположение о том, что обучение математике по реформированным рабочим программам способствует более осознанному использованию математического знания при изучении общепрофессиональных и специальных дисциплин. По согласованию с представителями выпускающих кафедр для каждой специальности выбирались учебные дисциплины, существенно «нагруженные» математическим аппаратом. Для каждой дисциплины была разработана комплексная лабораторная работа, состоящая из двух частей. Задания первой части были направлены на проверку остаточных знаний по математике, но сформулированы в терминах данной дисциплины. Задания второй части лабораторной работы проверяли знания уже непосредственно по самой дисциплине, но для своего выполнения требовали широкого использования математического аппарата.
Еще одним подтверждением выдвинутой гипотезы послужили результаты специально разработанных тестовых заданий, в которых оценивался уровень трансформации знаний. Уровень трансформации считается высшим уровнем усвоения знаний и характеризуется способностью переносить усвоенные знания с одной предметной области на другую, что в свою очередь, отражает сформированность высших уровней мышления (изоморфизм мышления). Процесс обучения математике и должен быть направлен на формирование структурно-аналитических компонент мышления.
Тестовое задание по каждой дисциплине состояло из трёх усложняющихся заданий. При ответе на первый вопрос студенты должны четко представлять, из каких разделов математики требуются знания для выполнения предлагаемой задачи по специальности. Во втором задании необходимо было установить соответствие между разделами курса математики и разделами изучаемой дисциплины. Третье задание предполагало переформулировку профессиональной задачи на язык математики. В качестве показателя успешности выполнения тестового задания был введен коэффициент трансформации, который измерялся по десятибалльной шкале.
Результаты выполнения тестового задания представлены на рис. 2.
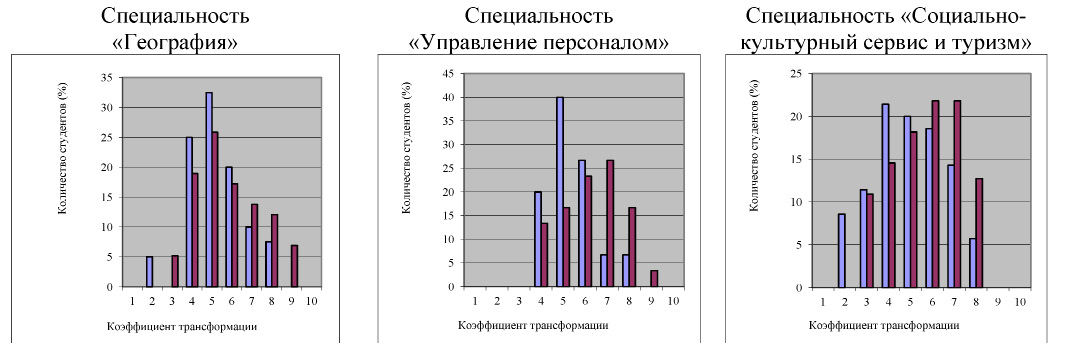
Рис. 2. Распределение коэффициента трансформации знаний:
![]() – контрольная группа;
– контрольная группа; ![]() – экспериментальная группа
– экспериментальная группа
По этому показателю наблюдались самые значительные расхождения: успешность выполнения 65,5 % в экспериментальной выборке и 36,2 % – в контрольной (приведены средние значения по трем специальностям). Этот результат можно напрямую связать с предлагаемыми нововведениями в структуру и содержание предметной подготовки по математике. Осознание студентами логических принципов, лежащих в основе построения курса математики, способствуют, на наш взгляд, формированию системного типа ориентировки в изучении последующих дисциплин. Целенаправленное включение профессионально-ориентированной компоненты в учебное содержание определенных видов учебных занятий по математике способствует созданию квазипрофессиональной среды и, тем самым, позволяет реализовать принцип осознанной перспективы в процессе изучения дисциплины.
В статье предложен дуальный подход к проектированию системы математического образования в системе бакалавриата для широкого спектра специальностей, обозначенных в статье, как «нематематические». Суть этого подхода заключается в следующем: содержание математического образования должно быть представлено как в логике современной математики, так и в логике будущей профессиональной деятельности студента. В таком случае целью учебной деятельности студента является не только овладение математическим аппаратом как целостной научной системой, но и формирование профессионально значимых видов деятельности на основе логики математики. Именно такой подход обеспечивает оптимальные условия для формирования познавательного интереса к высшей математике у студентов и, тем самым, создает предпосылки к эффективной организации процесса обучения математическим дисциплинам.
Все полученные результаты, их качественная и количественная (с применением методов математической статистики) интерпретации в целом подтвердили правильность выбранной образовательной стратегии по отбору профессионально-ориентированного содержания и последовательности его включения в рабочие программы по математике. Взаимодействие экспертов-математиков и экспертов-профессионалов привело к формированию рабочих программ по математике, в которых отражен фундаментальный характер образовательной области «Математика» и представлено профессионально-обоснованное прикладное содержание дисциплины.

