Scientific journal

International Journal of Applied and fundamental research

ISSN 1996-3955

ИФ РИНЦ = 0,593

Электромагнитное поле

Энергия электромагнитных волн. Электромагнитные волны переносят энергию. Объемная плотность энергии складывается из плотностей электрического ϖэл и магнитного ϖм полей:

ϖ = ϖэл + ϖм = ε ε0·Е2/2 + μ μ0·Н2/2, (1)

где ε и μ соответственно диэлектрическая и магнитная проницаемости среды, ε0 и μ0 – электрическая и магнитная постоянные вакуума, Е и Н – напряженности электрического и магнитного полей.

Учитывая, что

ϖэл = ϖм (2)

и 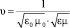, (3)

то ϖ = 2 ϖэл = ε ε0·Е2 = 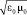··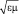Е·Н. (4)

Откуда получим:

I = ϖ·υ = Е·Н,

в вакууме:

I = ϖ·с, (5)

где с – скорость света в вакууме.

Это интенсивность электромагнитной волны или вектор плотности потока электромагнитной энергии, называемой вектором Умова-Пойнтинга:

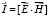. (6)

Вектор 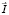направлен в сторону распространения электромагнитной волны, а его модуль равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространению волны, [I] = Вт/м2.

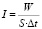, (7)

где W/Δt – мощность э/м излучения, переносимая через площадку S [1, 2].

Если в уравнении (5) для вакуума выразить ϖ только через одну величину, напряженность электрического поля

ϖ = ε0·Е2, (8)

то получим:

I = ε0·Е2·c. (9)

Давление электромагнитных волн. При падении на тела электромагнитные волны оказывают давление:

pэм = (1 + k)·ϖ (10), [pэм] = [ϖ] = Па,

k – коэффициент отражения электромагнитных волн, безразмерная величина,

k = 1 для зеркальной поверхности,

k = 0 для чёрной поверхности.

Из (9) и (10) вытекает:

I = p·c = (1 + k) ϖ·с. (11)

Гравитационное поле

Для гравитационного поля нам надо получить уравнения, аналогичные уравнениям (8), (9) и (10). Объемная плотность энергии гравитационного поля будет:

ϖг =g2/G, (12)

где g – напряженность гравитационного поля (ускорение свободного падения для планеты или звезды),

G – гравитационная постоянная.

Формула (12) аналогична формуле (8) для электрического поля в вакууме. Аналогия величин, входящих в формулы (8) и (12), приведена в таблице. Формула (12) вытекает из формулы (8). Положение G в знаменателе вытекает из сравнения закона Кулона и закона всемирного тяготения. Формула (13) для гравитационного поля легко может быть получена из формулы (9), а формула (15) – из формулы (10). Формула (14) вытекает из формулы (13) как доля интенсивности гравитационной волны космического тела при его взаимодействии с ядрами атомов второго космического тела. Обобщения использованных аналогий приведены в таблице.

Аналогии величин электрического и гравитационного полей

Мы считаем, что гравитационное поле переносится прямолинейно волновыми частицами этого поля – гравитонами. Сила гравитационного притяжения действует лишь на тяготеющие массы, в атомах – это ядра. На остальную площадь атомов вещества гравитационное поле не действует. Согласно планетарной модели атома площадь его ядра приблизительно в 1010 раз меньше площади атома, т.е. атом внутри пустой. Поэтому на второе тяготеющее тело от полной интенсивности действует лишь ее доля, определяемая долей площади ядер от площади атомов.

Выполним расчеты, используя формулы (13) и (14) для гравитационного поля, создаваемого Солнцем на его поверхности. Вообще-то предпочтительно использовать космические тела со значительно большей интенсивностью гравитационного поля (ориентировочно в десятки раз), но параметры Солнца измерены наиболее точно, и это обстоятельство явилось определяющим в нашем выборе.

Смысл формулы (14) заключается в том, что указанной доли интенсивности (Iд) гравитационного поля на поверхности Солнца достаточно, чтобы «погасить» вторую космическую скорость (υk) второго взаимодействующего тела.

Пусть вторым тяготеющим телом будет атом водорода, а точнее, его ядро – протон. Для формул (13) и (14) с учетом уравнения (7) очевидным является следующее соотношение: полная интенсивность гравитационного поля Солнца, пронизывающая атом водорода (Iг), во столько раз больше доли его интенсивности, пронизывающей ядро атома (Iд), во сколько раз площадь атома (Sa) больше площади ядра (Sя), т.е.:

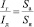, (16)

или:

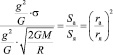
откуда

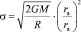. (17)

Здесь rа и rя – радиусы атома и ядра атома водорода соответственно. Напомним, что доля интенсивности (Iд) при взаимодействии гравитационного поля Солнца с ядром атома водорода приводит к гашению его второй космической скорости (υk), что отражено в уравнении (14).

Подставляя в (17) данные, получим:

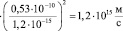. (18)

Используя выбранные нами взаимодействующие тела Солнце и ядро атома водорода, по уравнению (15) (см. таблицу) можно рассчитать коэффициент поглощения гравитационной энергии веществом (kг):

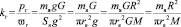,(19)

здесь 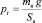, mя – масса ядра атома водорода (протона), R – радиус Солнца, M – масса Солнца. Подставляя в (19) данные, получим:

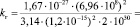
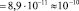. (20)

Как видно, коэффициент поглощения потока гравитационной энергии очень мал. Эффекты экранировки (поглощения) гравитационного поля были обнаружены экспериментально китайскими учеными (Вангом и его коллегами), которые зафиксировали относительное уменьшение напряженности гравитационного поля Солнца в 10–9 раз во время солнечного затмения в марте 1997 г. [3].

Поглощение телом гравитационной энергии и превращение ее в кинетическую энергию тела является неотъемлемой частью гравитационного взаимодействия.

Выводы

Полученное значение скорости распространения гравитационного поля 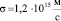соответствует «минимальному значению скорости тяготения 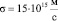» [4], полученному П.С. Лапласом «по вековому ускорению Луны». Это значение (18) намного превышает скорость света, которая принята в теории относительности за максимальную скорость. Также полученное значение (18) по использованной нами методике является заниженным, т.к. интенсивность гравитации может быть больше чем солнечная у звезд с большей массой и большей второй космической скоростью на их поверхности. Также следует отметить, что скорость гравитационного поля подобно скорости света является мировой константой и не должна зависеть от массы тяготеющего тела и интенсивности его гравитационного поля. Только очень большие массы (типа черных дыр) могут оказать заметный вклад в «гашение» скорости гравитации. Кстати, отметим, что черная дыра «гасит» свое световое излучение (скорость света), но не в состоянии «погасить» свое гравитационное излучение (скорость гравитации). Поэтому черные дыры за счет гравитационного излучения удерживают около себя звездную материю своих галактик. Из этого обстоятельства видно, что скорость гравитационного излучения значительно превышает скорость светового излучения, подтверждая наши расчеты и выводы.