Из Эмпирической Теории Вселенной (ЭТВ) [1–6] следует, что с каждым космическим телом связан стационарный гравитационный потенциал, представляющий собой суперпозицию гравитонов. Гравитон является носителем гравитационного взаимодействия и волновым пространством. Так как скорость волны не зависит от системы отсчета, то границы Вселенной расширяются с максимально возможной скоростью света (скорость гравитона существенно меньше скорости света), а каждая ее часть со скоростью пропорциональной относительному размеру. Например, если известна скорость удаления Луны от Земли DRM – E и расстояние между ними RM – E, то возраст Солнечной системы равен: t = RM – E/DRM – E млрд лет.
Поскольку стационарный гравитационный потенциал каждого космического тела связан с его массой, то при расширении пространства линейно растет масса тел. Причина удаления Луны от Земли одна – увеличение массы тел и связанное с этим расширение пространства. Само пространство является суперпозицией гравитонов и служит переносчиком взаимодействия. На самом деле космические тела не обмениваются виртуальными гравитонами (в пространстве, так как сами являются пространством), но наблюдаемые во Вселенной структуры стационарны (и при этом линейно расширяются) благодаря волновым свойствам пространства и наличию двух абсолютов – скорости света С и скорости гравитона Vg.
Теперь, чтобы вычислить прирост какого-либо параметра в Солнечной системе необходимо взять любой линейный размер или массу и разделить на возраст Солнечной системы t (10,1 млрд лет). Например, скорость удаления Земли от Солнца равна: DRE = RE/t =14,8 м/год, а скорость увеличения радиуса Земли – DrE = rE/t =0,63 мм/год. Здесь RE – средний современный радиус орбиты Земли, а rE – средний современный радиус Земли. Следует обратить внимание, что приросты постоянны по величине в течение всей эволюции Вселенной.
Линейный рост линейных размеров означает, например, что средний радиус орбиты Марса изменялся по закону RM = DRM∙t, где t – текущее значение возраста Солнечной системы. При определенных значениях текущего возраста t радиус орбиты Марса пробегал значения равные радиусу орбиты Венеры, Земли или современное значение. То есть современные значения параметров Венеры, Земли и Марса (если откладывать значение параметра от R) это в некотором роде эволюция самого Марса (если откладывать значение этого параметра от t). Для того чтобы получить законы эволюции планет необходимо знать современные параметры Венеры, Земли и Марса. Для получения законов эволюции параметров планет использовался метод наименьших квадратов.
При линейном росте линейных размеров и при линейном росте массы получаем следующую зависимость эволюции плотности материи: r ~ M/R3 ~ t–2 ~ R–2. Эта зависимость справедлива для Вселенной целиком, для каждого космического тела или для атмосферы планеты, а также для плотности излучения в единице объема пространства. Универсальность этого соотношения позволяет использовать его в качестве универсальной единицы измерения (y = f(t–2) или y = f(R–2)) при поиске законов эволюции планет (то есть в качестве единиц измерения для оси Х).
Цель данной работы состоит в том, чтобы найти общий закон эволюции температуры на твердой поверхности планеты и с его помощью вычислить эволюцию температуры на планетах: Венера, Земля [7] и Марс.
В работе [8] выполнен анализ температур на планетах Солнечной системы в предположении обогрева планеты Солнцем. Показано, что равновесная температура планеты не зависит от параметров самой планеты, но обратно пропорциональна корню квадратному от среднего радиуса орбиты. Температура на твердой поверхности планеты, обладающей атмосферой, существенно отличается от равновесной температуры. Если построить график разницы температуры поверхности планеты и ее равновесной температуры от давления атмосферы, то получим прямую зависимость при диапазоне давлений в 4 порядка (рис. 1).
Полученная зависимость хорошо согласуется с наблюдением, но не проходит через начало координат. Коэффициент детерминации R2 = 1 демонстрирует, что 100 % исходной информации объясняется полученным уравнением регрессии (приведено на рис. 1).
Исходные данные о Венере, Земле и Марсе собраны в табл. 1.
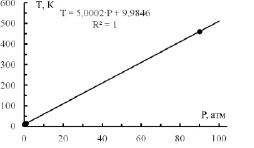
Рис. 1. Зависимость разницы температуры поверхности планеты и ее равновесной температуры от давления атмосферы
Таблица 1
Средние температуры планет и их физические параметры
|
№ п\п |
Параметр \ планета |
Венера |
Земля |
Марс |
|
1 |
T наблюдения, K |
753 |
288 |
208 |
|
2 |
T∙Δr2 |
275,6 |
114,3 |
24,0 |
|
3 |
Прирост радиуса планеты Dr, мм/год |
0,605 |
0,63 |
0,34 |
|
4 |
Радиус орбиты планеты R, а.е. |
1,082 |
1,496 |
2,279 |
|
5 |
R-2 |
0,854 |
0,447 |
0,193 |
|
6 |
Прирост радиуса орбиты DR, м/год |
10,71 |
14,81 |
22,56 |
|
7 |
ΔT |
460 |
15 |
10 |
|
8 |
Давление атмосферы, атм. |
90 |
1 |
0,0061 |
В табл. 1 R = DR∙t и DR обозначены соответственно средние радиусы орбит планет земной группы и приросты радиусов в год. Средние радиусы планет и их приросты обозначены соответственно r = Dr∙t и Dr.
На основании исходных данных табл. 1 проверим, сможет ли зависимость T = f(R) стать зависимостью эволюции температуры на Марсе (то есть зависимостью T = f(t)). С этой целью построена зависимость T = f(R) (строка 1 от строки 4 табл. 1) и по исходным точкам проведена степенная регрессионная зависимость (рис. 2).

Рис. 2. Зависимость темрературы на поверхности Венеры, Земли и Марса от радиусов их орбит
Рис. 2 демонстрирует довольно быстрый спад температуры от радиуса орбиты (показатель степени равен – 1,648) и низкий для закона коэффициент детерминации R2 = 0,894. Так как температура зависит от давления атмосферы, а плотность атмосферы быстро спадает с расширением планеты, то следует учесть разную скорость расширения указанных планет.
Выполненный выше поиск закономерностей полезен, но лучше искать соответствие между теорией (ЭТВ) и наблюдением. Поэтому на рис. 3 представлена зависимость средней температуры планеты (строка 1 табл. 1) от универсальной единицы измерения (строка 5 табл. 1 – ось Х). По исходным точкам указанной зависимости проведена линейная регрессия, проходящая через начало координат (современная собственная температура Земли равна 17,4 K [6] и несколько отличается от 0 K). Коэффициент детерминации высок, но не достаточен для признания полученной регрессии законом эволюции температуры еще и потому, что не учтено собственное различное расширение планет.
Поскольку радиус планеты линейно увеличивается, то при неизменных других условиях давление атмосферы уменьшается пропорционально r–2. На том же рис. 3 построена зависимость средней температуры планеты (строка 2 табл. 1) в зависимости от универсальной единицы измерения (строка 5 табл. 1 – ось Х) с учетом расширения планет. В этом случае точки всех трех планет легли на прямую линию очень точно (коэффициент детерминации R–2 = 0,9992), а уравнение регрессии имеет вид:
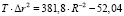 . (1)
. (1)
Коэффициент детерминации достаточно высок, чтобы считать полученную регрессию законом эволюции температуры на планетах с атмосферой. Однако в уравнении учитывается расширение планеты в левой части уравнения, а универсальные единицы учитывают свойства Вселенной справа. Кроме того, получено достаточно большое и отрицательное значение свободного члена в уравнении регрессии не имеющего смысла. Важно и то, что уравнение (1) невозможно преобразовать в достаточно простое уравнение T = f(t) или T = f(t–2) имеющее смысл. Таким образом, уравнение (1) не годится в качестве закона эволюции температуры планет.

Рис. 3. Зависимость средней температуры на поверхности планеты от универсальной единицы R–2. Линейная регрессия проходит через начало координат (черные кружки и жирная прямая линия). Зависимость средней температуры планеты в универсальных единицах с учетом расширения самой планеты (светлые кружки и тонкая прямая линия)
Если через точку температуры Земли (на рис. 3) и начало координат провести прямую линию, то уравнение регрессии для Земли имеет вид:
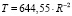 . (2)
. (2)
Аналогичные зависимости для Венеры и Марса имеют вид соответственно: T = 881,7∙R–2 и T = 1080,7∙R–2. Переход к функции температуры в зависимости от возраста осуществляется простой заменой R–2 → t–2 и вычислением коэффициента из условия нормировки функции на современное значение температуры (лучше в привычных градусах Цельсия). Соответствующая зависимость эволюции температуры для Земли приведена на рис. 4.

Рис. 4. Эволюция средней температуры на поверхности Земли. Вертикальная полоса отражает период образования твердой коры (материков)
Возраст Солнечной системы был вычислен по удалению Луны от Земли и составил 10,1 млрд лет, что близко к возрасту Вселенной и сильно отличается от общепризнанных датировок возраста планет. Исходя из этого возраста, вычислены все приросты линейных размеров в табл. 1. Теперь, зная приросты, по полученному уравнению (2) вычислена средняя температура на твердой поверхности планеты Земля в любом возрасте (рис. 4) в привычных координатах (градусы Цельсия – возраст планеты). Вертикальной градиентной линией отмечен «возраст формирования Земли» (твердой поверхности – материков) в соответствии с современными датировками. Расчетные температуры в этот период эволюции Земли свидетельствуют о том, что планета находилась в полностью расплавленном состоянии (более 4,2 млрд лет назад). Радиус планеты в этот период был почти в 2 раза меньше современного, также как и радиус орбиты. Очевидно, что наблюдаемые древние гигантские кольцевые структуры на поверхности материков – это застывшие магматические пузыри.
В данной статье получен закон эволюции средней температуры на твердой поверхности планет с атмосферой на основе физических данных Венеры, Земли и Марса, но сам закон можно распространить на любую аналогичную планету во Вселенной. Сама Солнечная система не уникальна во Вселенной, также как элемент в периодической системе атомов.

