Scientific journal

International Journal of Applied and fundamental research

ISSN 1996-3955

ИФ РИНЦ = 0,593

Одной из важных и актуальных задач в различных отраслях промышленности и энергетике является повышение эффективности проводимых процессов. Например, повышение эффективности теплообмена может выполняться с помощью как активных, так и пассивных методов. К пассивным методам относятся – создание искусственной шероховатости поверхности, выступы, кольцевые накатки, закрутка потока в канале и т.д. При этом одной из основных задач является определение коэффициентов теплоотдачи от таких поверхностей. В данной статье рассмотрен приближенный подход определения средних коэффициентов теплоотдачи в каналах с шероховатой стенкой и закруткой потока. Для этого используется модель пограничного слоя с функцией турбулентной вязкости Дайслера с учетом затихания турбулентных пульсаций по модели Ландау и Левича.

Приближенное математическое описание процессов переноса в пограничном слое связано с моделями Прандтля, Кармана, Ландау и Левича, и др., а также с развитием гидродинамической аналогии Рейнольдсом и Чилтоном – Кольборном. Причем наиболее теоретически обоснованной и перспективной является модель диффузионного пограничного слоя Ландау – Левича [3 ,8, 9]. Известно, что турбулентный пограничный слой, как и всякая устойчивая статистическая система, имеет некоторые консервативные свойства [5, 6, 11]. На важную особенность пристенной турбулентности – весьма слабую зависимость некоторых характеристик осредненного течения по отношению к внешним возмущениям – особое внимание обратил С.С. Кутателадзе совместно с А.И. Леонтьевым. На основе предельных относительных законов теплообмена и трения были созданы расчетные методы [5–7].

Теоретическая основа рассмотренного ниже подхода заключается в использовании известных свойств консервативности законов трения к продольному градиенту давления в пограничном слое, т.е. структура математического описания элементарных актов переноса инвариантна к различным возмущениям и масштабу аппарата. Влияние этих факторов не изменяет структуру математического описания пограничного слоя, а учитывается параметрически [3, 8, 9].

Определение коэффициентов теплоотдачи

Допущения к математической модели теплоотдачи:

– входной участок значительно меньше длины обтекаемого тела (канала) и поэтому им можно пренебречь. При небольшой длине канала влияние входного участка можно учесть известными поправками;

– теплофизические свойства среды поперек пограничного слоя изменяются незначительно. При больших градиентах температур влияние можно учесть известными поправками;

– турбулентное число Прандтля близко к единице;

– основное сопротивление процессу теплоотдачи сосредоточено в пограничном слое, где происходит молекулярный перенос тепла в сочетании с затухающей турбулентной диффузией (модель Ландау-Левича).

Сопротивление переносу тепла в турбулентном пограничном слое записано в виде [8, 9]:

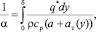(1)

где α – средний коэффициент теплоотдачи, Вт/ (м2·К); q* – относительная плотность теплового потока; ρ – плотность среды, кг/м3; cp – теплоемкость среды, Дж/(кг К); a, aт – коэффициенты молекулярной и турбулентной температуропроводности, м2/с; δ – толщина пограничного слоя, м; y – поперечная координата, м.

Коэффициент турбулентного переноса aт = vт/Prт, принят в форме функции Дайслера [11]

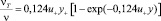, (2)

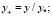
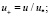
где 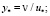u* – динамическая скорость, м/с; v – коэффициент кинематической вязкости, м2/с, /Prт = vт/aт – турбулентное число Прандтля; vт – коэффициент турбулентной вязкости, м2/с, (Prт ≈ 1).

После интегрирования (1) с функцией (2) получена формула для коэффициента теплоотдачи при осевом движении потока в канале в виде:

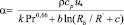, (3)

где безразмерные величины связаны с областью интегрирования и установлены в виде:

k = 13,91; b = 2,5; R’ = 30; с = 0,14; Pr – число Прандтля.

Показатель степени при числе Прандтля Pr0,66 следует из закона затухания турбулентных пульсаций в пограничном слое.

Уравнение (3) является достаточно общим и позволяет определять коэффициенты теплоотдачи для различных условий турбулентного движения среды при соответствующих вычислениях его параметров.

Теплоотдача от пластин в трубе

Первоначально выполним проверку уравнения (3) для пластины и трубы.

При движении среды в турбулентном режиме вдоль плоской поверхности параметры уравнения (3) имеют вид [7, 11]:

динамическая скорость:

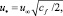(4)

коэффициент трения:

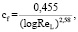(5)

число Рейнольдса:

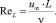(6)

где u∞ – средняя скорость среды, м/с; L – длина пластины, м.

Значение средней безразмерной толщины пограничного слоя Rδ можно определить по следующим формулам [11], [8]:

Rδ = exp[0,4(u∞/u*–5,0)], (7)

или 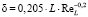, (8)

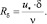(9)

Выражение (7) следует из логарифмического профиля скорости при u = u∞, у = δ.

На основе (3) запишем число Нуссельта NuL для пластины:

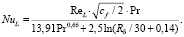(10)

Для проверки адекватности полученных значений чисел Нуссельта произведем их сравнение со значениями чисел Нуссельта по следующему известному уравнению:

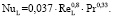(11)

Результаты расчета чисел Нуссельта по полученным значениям Rδ, которые были рассчитаны по (7) и (9) представлены в табл. 1 и табл. 2 соответственно. Длина пластины 1 м.

Таблица 1

Значения чисел Нуссельта в зависимости от числа ReL

Таблица 2

Значения чисел Нуссельта в зависимости от числа ReL

На основании результатов расчета чисел Нуссельта по (10) и (11) можно сделать вывод, что их значения имеют удовлетворительную сходимость от 0,4 % до 16,2 % при значениях средней безразмерной толщины пограничного слоя Rδ рассчитанной по (7) и от 2,7 % до 15,6 % при Rδ рассчитанной по (9).

Для круглой трубы с гладкими стенками при осесиметричном движении среды динамическая скорость и Rδ в уравнении (3) имеют вид:

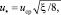(12)

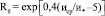, (13)

где ξ – коэффициент гидравлического сопротивления; ucp – средняя скорость, м/с.

Значение средней безразмерной толщины пограничного слоя Rδ можно вычислить по формуле (7) при u∞ = ucp. В качестве примера определим Rδ используя безразмерный профиль скорости в виде:

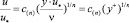, (14)

где c = 8,74, n = 7.

На границе вязкого подслоя при у = δ1 функция, (14) имеет значение:

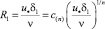. (15)

Отсюда запишем:

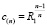. (16)

При у = δ из (15) имеем:

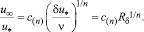(17)

Тогда

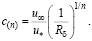(18)

В результате из (15) и (17) получим:

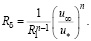(19)

Для пластины 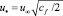и тогда:

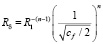(20)

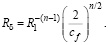или (21)

При R1 =11,6 получим (n = 7)

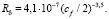(22)

Аналогично получим для трубы:

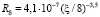. (23)

Расчеты по формулам (13) и (23) дают близкие значения Rδ. Уравнение (3) для трубы в безразмерной форме запишется в виде

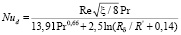. (24)

Для сравнения результатов расчетов числа Нуссельта (Nud = αd/λ) по (24) использовалась известная формула для трубы:

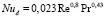, (25)

а также уравнение Петухова:

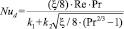, (26)

где k1 = 1+ 3,4ξ; k2 = 11,7 + 1,8Pr–1/3, ξ – по формуле Блазиуса:

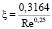, (104 < Re < 105). (27)

Значения чисел Нуссельта представлены в табл. 3.

Таблица 3

Значения чисел Нуссельта от чисел Рейнольдса (Pr = 5)

В выражении (24) можно ввести известный множитель (Pr/Prст)0,25, который учитывает зависимость физических свойств жидкости от температуры и влияние направления теплового потока.

Теплоотдача для поверхностей с элементами интенсификации

Следует отметить, что выражения для чисел Нуссельта, аналогичные (10) и (24) были получены различными авторами еще 1950–70 гг., поэтому определение коэффициентов теплоотдачи для пластины и трубы с гладкой поверхностью не имеет особой новизны. Значительно более сложной задачей является определение теоретическим путем коэффициентов теплоотдачи для поверхностей с элементами интенсификации (шероховатость, выступы, кольцевые накатки, закрутка и т.д.). В настоящее время для этого используются в основном различные полуэмпирические подходы.

Рассмотрим применение выражения (3) для закрученного потока при стационарном режиме.

Среднее значение динамической скорости в закрученном потоке следует из условия баланса сил в канале:

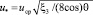, (28)

где ucp – средняя скорость в канале, м/с; θ – угол закрутки потока; ξ3 – коэффициент сопротивления потока с закруткой.

В пограничном слое с возмущениями (интенсификаций) параметры уравнения (3) имеют вид [8, 9]:

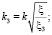
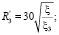
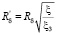. (29)

где ξ – коэффициент сопротивления для осесимметричного потока, вычисляется по известному выражению, например (27). Запишем выражение (3) в более удобном для расчетов виде. Используя значения (28), (29), получим число Нуссельта:

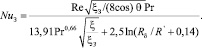(30)

Аналогично запишем число Стантона 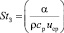для канала с закруткой:

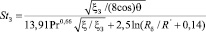. (31)

Полученные выражения также можно использовать для приближенных расчетов коэффициентов теплоотдачи в каналах с шероховатой поверхностью. Динамическая скорость в каналах с шероховатой поверхностью примерно равна

,

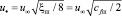где ξш, сfш – коэффициенты гидравлического сопротивления и трения с учетом шероховатости. Известно, что в режиме максимального проявления шероховатости наступает автомодельный режим и ξш ≈ 0,08.

Число Стантона для канала с шероховатой стенкой запишется в виде:

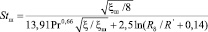. (32)

Результаты расчетов

Для расчета коэффициента гидравлического сопротивления закрученных потоков в работах [1, 2, 7, 11] представлены различные выражения и графики. На рис. 1 даны результаты расчета числа Нуссельта (30) и сравнение с обобщенными опытными данными для закрученного потока [11] Расхождение в пределах 10 %. Также удовлетворительное согласование (± 15 %) получено с экспериментальными данными, приведенными в работе [2].

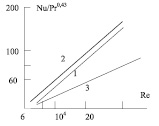
а)

б)

Рис. 1. а) зависимость комплекса Nu/Pr0,43 от числа Re в канале с ленточным завихрителем: 1 – расчет по уравнению (30); 2 – экспериментальные данные; 3 – для осевого потока; б) результаты расчета и опытные данные по теплоотдаче в канале с шероховатыми стенками 1,3 – расчет по уравнению (32), 2,4 –экспериментальные данные [4]

Рис. 2. Эффективность интенсификации теплообмена в круглом канале [2], [9]: 1 – область, занимаемая экспериментальными точками, 2 – при Nu/Nu0 = ξ/ξ0, 3 – расчет по формуле (30)

На рис. 2 представлена зависимость Nu/Nu0 от ξ/ξ0 для различных способов интенсификации теплообмена в каналах и результаты расчета с использованием формулы (30), где Nu0, ξ0 для каналов без интенсификации. Из рис. 2 следует, что рекомендуемое многими авторами отношение Nu/Nu0 = ξ/ξ0 справедливо до значения ξ/ξ0 ≤ (1,5÷2). При ξ/ξ0 > 2 начинается опережающий рост гидравлического сопротивления по сравнению с теплоотдачей.

Выводы

На основе применения модели турбулентного пограничного слоя получено выражение для расчета среднего значения коэффициента теплоотдачи. Выполнена последовательная проверка данного выражения для случаев теплоотдачи от пластины, в трубе, а также в каналах с закруткой потока и шероховатой стенкой. При переходе к потокам с возмущениями выполняется корректировка параметров уравнения в виде отношения коэффициентов гидравлического сопротивления.

Полученные выражения для чисел Нуссельта и Стантона рекомендуется для практического применения при расчетах теплообменных аппаратов.

Работа выполнена в рамках проектной части государственного задания в сфере научной деятельности (Задание № 13.405.2014/К).