Понятие об упругих столкновениях играет важную роль в физике, поскольку со столкновениями часто приходится иметь дело в физическом эксперименте в области атомных явлений, и обычные столкновения можно часто с достаточной степенью точности считать упругими [3, 9, 10]. Состояние газа определяется взаимодействием молекул между собой и с границами твердыми или жидкими телами. При взаимодействии частиц могут происходить различные процессы. Процесс столкновения сводится к изменению свойств частиц в результате взаимодействия. Законы сохранения позволяют достаточно просто устанавливать соотношения между различными физическими величинами при столкновении частиц.
Кинетическое уравнение столкновения молекул
Известное интегродифферециальное кинетическое уравнение Больцмана для парных столкновения имеет в виде [1, 5, 7]
.
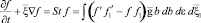f (t, x, y, z, xx, xy, xz) – функция распределения молекул по времени, координатам и скоростям, f ′, f1 ′ – функции распределения, соответствующие скоростям молекул после столкновения x′ и x1′, g – относительные скорости молекул при парных столкновениях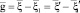 
, b, e – прицельное расстояние и азимутальный угол при столкновениях частиц.
Рассмотрим определение скорости парных упругих столкновениях молекул. Столкновение молекул в совершенном газе являются парными, т. е. столкновении участвуют только две молекулы. Упругое столкновение определяется как столкновение, в котором не происходит обмена между поступательной и внутренней энергиями. Скорости двух молекул до столкновения в типичном парном столкновении можно обозначить через x1 и x2, а после столкновения x1′ и x2′.
В процессе столкновении должны сохраняться массы, импульс, энергии и момент инерции и означает, что
,
,
,
,
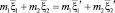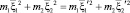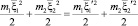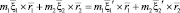здесь m1, m2 – массы двух молекул. Значения относительной скорости между молекулами до и после столкновения можно определить так:
, 
.
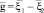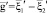уравнения можно разрешить относительно x1 и x2, скорости до столкновений могут быть выражены в виде
,
,
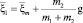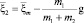где скорости центр масса
,
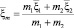Скорости до столкновения относительно центра масс ξ1–ξm и ξ2–ξm показывают, что эти скорости параллельны в системе центра масс, и если молекулы являются точечными центрами сил, то сила между ними остается в плоскости, содержащей эти скорости. Столкновение, следовательно, происходит в плоскости, проходящей через начало системы центра масс. Так и скорости молекул после столкновении можно написать
,
,
.
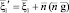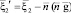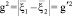где n – случайный единичный вектор
, 
.
, 
.
.
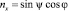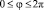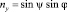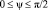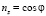Следуя формализму Гиббса, рассматривают не одну систему, ансамбль систем в 6N мерном Г-пространстве, распределённых в соответствии с N – частичной функцией распределения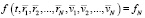 
, имеющей смысл вероятности нахождения системы в момент времени t в точке 
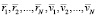в окрестности 
.
.
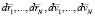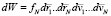Подобный ансамбль описывается известным уравнением Лиувилля:
,
.
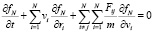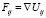И вот с этого момента уравнение Лиувилля и все последующие кинетические уравнение, следующие из цепочки Боголюбова, включая последнее её звено – уравнение Больцмана, имеют вероятностную природу. И хотя уравнение проще системы уравнения эволюции, оно учитывает N частичные столкновения молекул и также чрезвычайно сложно для практического анализа. Переход на менее детальный уровень описания связан с дальнейшим огрублением описания системы с помощью s – частичных функций распределения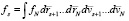 
, определяющих вероятность одновременного обнаружения s частиц независимо от состояния остальных N-s частиц.
Следуя идеям Боголюбова, получают цепочку зацепляющихся уравнений:
,
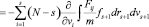для двойных столкновений можно написать в виде
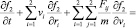
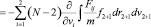
и для тройных
.
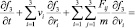
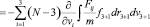Вплоть до одночастичной функции распределения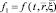 
газа Больцмана с учётом лишь парных столкновений:
.
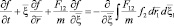Следуя Больцману, будем считать молекулы сферически симметричными, и принимая гипотезу молекулярного хаоса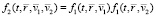 
, и приходим к уравнению Больцману.
С учетом статистической независимости частиц перед столкновением решение уравнения есть [4]
.
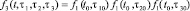где ta0 = ta0 (t, t0, t1, t2, t3) - значения координат и импульсов, которые частиц должны иметь в момент t0 для того, чтобы к моменту t попасть в заданные точки t1, t2, t3 фазового пространства.
Теперь перейдя от функций f1 к функциям f = Nf1, найдем кинетическое уравнение в виде
,
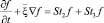где
,
.
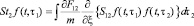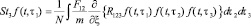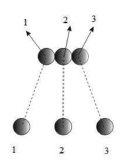
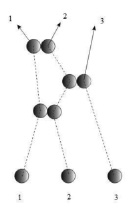
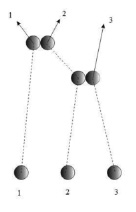
а) б) в)
Рис. 1. Основные траектории частиц тройных столкновений молекул
Первый из этих интегралов есть интеграл двойных, а второй – тройных столкновений. Здесь S12 и R123 – некоторые операторы. Рассмотрим несколько процессов столкновений, учитываемых интегралом. Прежде всего, оператор R123 обращается в нуль, если хотя бы одна частиц не взаимодействует с остальными. В число процессов, для которых R123 ≠ 0, входят не только тройные столкновения, но и совокупности нескольких двойных. Посмотрим несколькие виды столкновения.
На рис. 1, а изображен, что три частицы одновременно вступают в «сферу взаимодействия». Но оператор R123 отличен от нуля также и для таких процессов «тройных взаимодействий», которые сводятся к трем последовательным двойным столкновениям, причем одна из пар частиц сталкивается между собой дважды, такого процесса изображен на рис. 1, б. Более того, оператором R123 учитываются также и случаи, когда одно (или более) из трех столкновений является «воображаемым», т.е. возникающим, лишь если не учитывать влияния на траекторию частиц какого-либо из реальных столкновений, который изображен на рис. 1, в.
В процессе тройных столкновений должны сохраняться массы, импульс, энергии и момент инерции [2, 6].
,
,
,
.
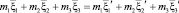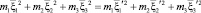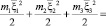
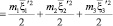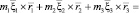
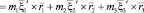Скорости частиц после тройных столкновений имеет вид
, 
,
, 
,
, 
.
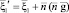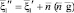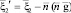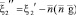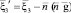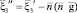Скоростное отношение до и после столкновения равны
.
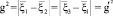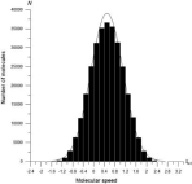
Рассмотрим нескольких результатов, полученных из функции распределения молекул. Число частиц использовал 9×105 в этой сосуде. Из графиков ясно, что скорости молекул до и после столкновения совпадали. На рис. 2 а, б, в показаны скорости молекул до столкновения и на рис. 3 а, б, в после столкновения.
Заключение
Тройное столкновение может иметь место, когда молекула столкнется с парной молекулой [11–14]. Упругое столкновение определяется как столкновение, в котором не происходит обмена между поступательной и внутрнней энергиями. Хотя потенциал Леннарда-Джонса и используется при моделировании жидкости и твёрдых тел, строго говоря, взаимодействие молекул при больших плотностях уже не является парным. В конденсированных средах на рассматриваемую пару молекул влияют молекулы окружения. Так было найдено, что для твёрдого аргона вклад в энергию от тройных взаимодействий может достигать 10 процентов [8]. Однако, учет тройных взаимодействий вычислительно слишком дорог, поэтому обычно довольствуются неким эффективным парным потенциалом, где параметры e и σ отличаются от таковых для разреженных газов.
Работа выполнена при поддержке Российского Научного Фонда (Проект № 14-11-00709).
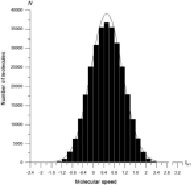
а) б)
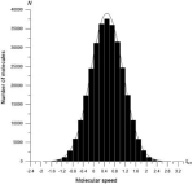
в)
Рис. 2. Распределение скорости молекул до столкновения
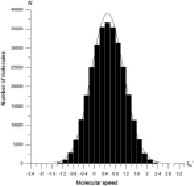
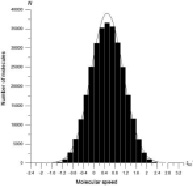
а) б)
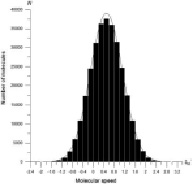
в)
Рис. 3. Распределение скорости молекул после столкновения