Вопросу теоретического описания турбулентных явлений посвящено множество монографий и научных статей, так как эта проблема оказывается неувядающей вот уже в течение более 150 лет. Время от времени появляются очень яркие новые идеи и методы, которые вдохновляют многочисленных исследователей на преодоление необычайных трудностей, связанных с пониманием сути проблемы. Тем не менее практическая важность хотя бы инженерного решения этой проблемы породила огромное число полуэмпирических моделей, в которых вопрос о сути проблемы не ставится, а делается подгонка результатов под определенный набор практически важных течений. При этом делается упор на описание средних моментов низкого порядка: средняя скорость, среднее давление, средняя кинетическая энергия, средние концентрации химических компонентов и т.п. Кроме того, развивалось моделирование, мотивацией которого была невозможность точного численного описания течений с очень большими числами Рейнольдса.
В свое время еще Прандтль обратил внимание на то, что имеется физическая аналогия между разреженным газом и турбулентной жидкостью. В качестве обобщения применения кинетических моделей в работе О.М. Белоцерковского, В.Е. Яницкого [1] была рассмотрена кинетическая модель описания турбулентности при помощи функции распределения, в которой аргументом является не молекулярная скорость x, как в разреженном газе f = (t, r, x), а v – пульсации скорости жидкой частицы f = (t, x, v). Тогда уравнение для функции распределения f = f(t, x, v) описывается уравнением Онуфриева–Лундгрена [6, 7] для одномерного случая
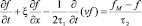(1)
здесь v = x − u – пульсационная скорость, а u = <x> – средняя скорость потока. Функция
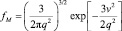
является плотностью вероятностей нормального закона распределения пульсаций скорости,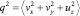 
– удвоенное среднее значение удельной кинетической энергии этих пульсаций E. Уравнение (1) очень похоже на модельное кинетическое уравнение Крука [5]:
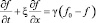(2)
где g – чистота столкновений. Форма уравнения для сплошносредных пульсаций (1), аналогичная кинетическому релаксационному уравнению, подкупает тем, что открывает возможность использовать аппарат методом Монте-Карло, хорошо развитый в динамике разреженных газов [2, 3, 8, 12, 13].
Модель описания турбулентности
В качестве обобщения применения кинетических моделей в сплошной среде была сделана попытка описания турбулентных явлений. В частности, исследовался пример диссипации турбулентного пятна. Здесь, как и в динамике разреженного газа, решается проблема на уровне функции распределения. Только теперь аргументом является не молекулярная скорость x, а пульсации скорости жидкой частицы v. Еще Прандтль обратил внимание, что имеется аналогия между разреженным газом и турбулентной жидкостью.
В модели Яницкого каждая частица в ячейке имеет новое качество (таблица). Жидкая частица, как и прежде, характеризуется физическими координатами и скоростью. Для этой функции распределения предлагается модель кинетического уравнения, аналогичная модельному уравнению в динамике разреженных газов.
1965. – V. 22, № 4. – P. 625–656.
Описание среды посредством функции распределения
|
Динамика разреженного газа |
Турбулентность |
|
Частицы |
|
|
Молекулы ri, координаты молекул ci, скорости молекул |
Жидкие частицы xi, координаты частиц vi, скорости пульсаций |
|
Функция распределения |
|
|
Для молекул f = f(t, r, c)
|
Для жидких частиц f = f(t, x, v)
|
|
Моменты |
|
|
(c–u), тепловая скорость |
(v–u), флуктуации |
, плотность
, нормировка
, макроскопическая скорость
, средняя скорость
Для описания турбулентности используется релаксационное кинетическое уравнение Онуфриева–Лундгрена [6, 7]. Главная цель рассмотрения состояла в сохранении основных принципов прямого статистического моделирования.
Задача о диссипации турбулентного пятна
Численно решалась задача о диссипации пятна, чья энергия первоначально сконцентрирована в области с характерным радиусом r0, рис. 1, характерный радиус пятна r*(t) и плотности турбулентной энергии Em (t) в центре пятна. Начальные данные:
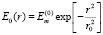
f (0, r, v) = f0 (z, v)
.
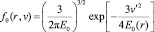Сравнение с экспериментальными данными приведено на рис. 2 (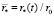
, 
).
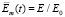Рис. 1. Диссипация турбулентного пятна (начальная область)
Кинетические модели турбулентности более информативны, так как они описывают пульсации на уровне функции распределения. Подобный подход к описанию турбулентности представляется перспективным, поскольку позволяет учитывать крупномасштабные турбулентные процессы непосредственно от схем уравнений переноса, а мелкомасштабные пульсации с помощью прямого статистического моделирования.
Интерференция турбулентных пятен
В рамках выше описанной модели Белоцерковского-Яницкого-Онуфриева решалась задача о взаимодействии эволюционирующих турбулентных пятен. Соответственно физическим процессам схема моделирования эволюции модели на малом временном интервале Dt, представляет собой последовательность трех этапов [2, 4].
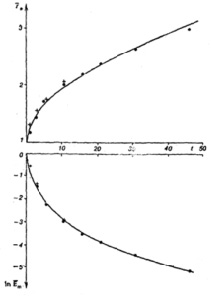
Рис. 2. Диссипация турбулентного пятна. ---- данные эксперимента (Naudasher), + прямое моделирование)
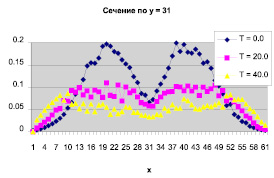
Рис. 3. Взаимодействие двух тубулентных пятен (распределение энергий) [9–11]
Ввиду большого вычислительного объёма задачи моделирование проводилось на многопроцессорной системе МВС-1000. Распараллеливание алгоритма осуществил аспирант А. Букин. Суть алгоритма, как для всех вариантов методов Монте-Карло довольно проста. На всех процессорах независимо друг от друга организовывается статистическое моделирование. По истечение времени установления решение усредняется по всем процессорам. На рис. 3 показаны распределения удельной энергии взаимодействующих пятен по времени t = 0, 20, 40 с по оси y.
Представлены графики зависимости энергии в центре пятна в зависимости от времени. На рис. 4 представлена зависимость логарифма отношения энергии в центре к его начальному значению от времени полученная из нашего эксперимента, а так же этаже зависимость, полученная из лабораторных экспериментов Наудашера [14]. На рис. 5 показаны отнормированные кривые удельной энергии в момент времени t = 0 и t = 34. Как видно, происходит «расползание» пятна вдоль радиуса.
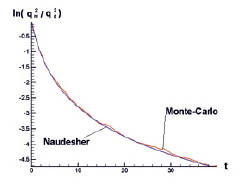
Рис. 4.
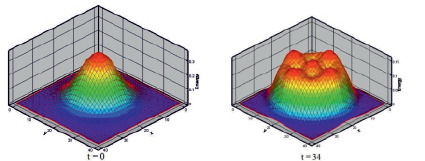
Рис. 5. Распределение удельной энергии в турбулентном пятне (t = 0 и t = 34) [9–11]
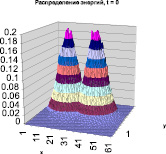
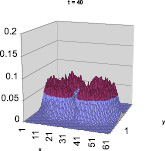
Рис. 6. Распределение удельной энергии при интерференции двух пятен [9–11]
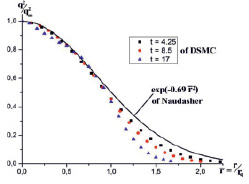
Рис. 7. Распределение энергии по относительному радиусу пятна
Это обусловлено смещением более быстрых частиц из центра к краям области. На рис. 6 приведено распределение удельной энергии пульсаций, при интерференции двух турбулентных пятен. В расчёте также получено распределение энергии по радиусу пятна в моменты времени t = 4.25, 8.5, 17 и сравнены с экспериментом Наудашера [14] (рис. 7).
Выводы
В результате проведенной работы был реализован алгоритм статистического моделирования и исследован применительно к задаче о турбулентном пятне. Тестовые задачи были обсчитаны на многопроцессорном компьютере MVS-1000 в Институте Автоматизации Проектирования РАН. Решены задачи о диссипации турбулентного пятна (проблему можно интерпретировать как дальний след в несжимаемой жидкости) и интерференции двух пятен.
Работа выполнена при поддержке Российского фонда фундаментальных исследований (РФФИ проект № 14-07-00564 А).