Конвективный теплообмен между телом и средой (жидкостной, воздушной) описывается системой уравнений гидродинамики, включающей в себя уравнения Навье-Стокса, непрерывности и переноса энергии. Эти уравнения чрезвычайно сложны и их решению (аналитическому, численному) посвящено огромное число работ. Многие работы рассматривают многочисленные частные случаи и их решения применительно к конкретным условиям [2, 3, 9]. Часть работ анализирует стохастический характер течений жидкости [4, 11, 12]. Для того, чтобы иметь возможность моделировать сложные реальные процессы конвективного теплообмена, во многих работах прибегают к допущениям, упрощающим математическую модель и ее решение.
Одно из таких принципиальных упрощений, получившее широкое распространение в инженерной практике, постулирует закон конвективного теплообмена между твердым телом и средой в форме линейной связи между потоком тепла от тела в среду P и разностью температур Tw – Ta поверхности нагретого тела Tw, с площадью теплообмена S, и среды Ta. Этот закон конвективного теплообмена, называемый еще линейным уравнением Ньютона, основывается на концепции коэффициента теплоотдачи (КТО), согласно которой коэффициент теплоотдачи α включает в себя всю сложность конвективного теплообмена и зависит от большого числа разнообразных физических и геометрических факторов, а также условий и режимов, в которых протекают процессы конвекции в конструкции реальной системы. Линейное уравнение Ньютона конвективного теплообмена имеет вид [4, 6, 7, 10] P = α S (Tw – Ta). На практике, для изучения процессов конвективного теплообмена, протекающих в реальных конструкциях, а также для получения значений коэффициента теплоотдачи, прибегают в каждом данном конкретном случае к проведению сложных и трудоемких экспериментальных исследований, с последующей обработкой полученных экспериментальных данных методами теории подобия [3, 10].
Вместе с тем конвективное взаимодействие не описывается концепцией КТО и зачастую приводит к неадекватным результатам в практике теплового моделирования и проектирования тепловых режимов систем. Для повышения адекватности моделирования конвективных процессов теплообмена в системах, необходимо заменить концепцию КТО подходом, основанном на концепции сопряженного конвективного теплообмена, согласно которой в результате взаимодействия температурных полей тела и омывающей ее среды необходимо решать совместно уравнения распространения тепловых потоков в твердом теле и в жидкости, а также уравнения движения среды Навье-Стокса.
В данной статье формулируются уравнения математической модели конвективного теплообмена в сопряженной постановке применительно к воздушной среде. В статье также приводится подход, позволяющий получать замкнутые аналитические решения конвективного теплообмена для вертикальной одномерной пластины. Полученное решение может быть использовано в программных комплексах теплового проектирования систем [8].
Математическая модель сопряженного конвективного теплообмена
Сопряженная постановка задачи конвективного теплообмена характеризуется тем, что в отличие от простой несопряженной постановки, к традиционным уравнениям Навье-Стокса, переноса энергии и неразрывности добавляются уравнения теплопроводности в твердом теле, а также граничные условия 4 рода, выражающие равенство температур и тепловых потоков в каждой точке соприкосновения жидкости и тела.
Рассмотрим свободную конвекцию в воздушную среду, Пренебрежем изменением плотности воздушной среды под влиянием изменения давления, но изменением плотности из-за неравномерности нагретого воздуха пренебрегать нельзя. Уравнения математической модели считаются стационарными и не зависящими от времени. Координата x, направлена вертикально вверх, координата y перпендикулярна пластине, вдоль координаты z изменения температурного поля и поля скоростей в среде отсутствуют. Для пограничного слоя, давление р’ = 0, vz = 0, ∂/∂z = 0 для плоскопараллельного потока, получим:
– уравнение Навье-Стокса в воздушной среде
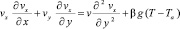, (1)
– уравнение переноса энергии в воздушной среде
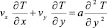, (2)
– уравнение непрерывности воздушной среды
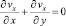, (3)
– уравнение теплопроводности пластины (∂2Tw/∂z2 = 0)
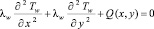, (4)
– граничные условия для скоростей воздуха:
vx = vy = 0 (y = 0);
vx = 0,
T = Ta (для y вне пограничного слоя), (5)
– граничные условия 4 рода:
,
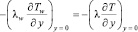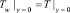(6)
где vx и vy – скорости воздуха вдоль осей x и y соответственно; T = T (x, y) и Tw = Tw (x, y) – распределения температуры в воздушной среде и пластине соответственно; Q (x, y) – объемная плотность распределения интенсивностей источников теплоты в пластине; Ta – температура воздуха за пределами пограничного слоя; Q – объемная плотность внутренних источников теплоты в теле; Ta – некоторые постоянные средние значения температуры в жидкости; Tw – трехмерное температурное поле в теле; ν – кинематическая вязкость, a = λ/ρc – температуропроводность, теплопроводность λ, плотность ρ, удельная теплоемкость c, температурный коэффициент расширения β среды; λw – теплопроводность материала тела; g – ускорение свободного падения; n – нормаль к поверхности тела.
Математическое моделирование свободного конвективного теплообмена вертикальной пластины со средой в сопряженной постановке
Рассмотрим теплообмен между вертикальной пластиной с внутренним источником теплоты и средой. Согласно концепции сопряженного моделирования конвективного теплообмена между телом и средой, сначала следует найти распределения температуры в теле Tw и среде T, при некоторых пока неизвестных тепловых потоках qw, q и температурах Tw и T на границе их раздела, а затем сшить полученные решения с помощью граничных условий четвертого рода, приравняв в каждой точке границы тепловые потоки и температуры как со стороны тела, так и со стороны среды.
Температурное поле пластины. Направим ось x вертикально вверх вдоль пластины, ось y – перпендикулярно пластине (горизонтально), а ось z – вдоль пластины в горизонтальном направлении. Распределение источников тепла будем считать равномерным по объему пластины. Это означает, что температурное поле не изменяется в пластине (на длине lz) и среде вдоль оси z, изменяется в пластине по оси y и изменяется в среде по осям x и y; другими словами температурное поле пластины одномерно, а среды – двумерно [1, 4–7].
Математическая модель свободной конвекции между вертикальной одномерной пластиной и двумерной средой описывается уравнениями (1)–(6), за исключением уравнения теплопроводности в пластине (4), в котором должен отсутствовать член со второй производной по координате x, в силу одномерности температурного поля пластины. Примем, что торцы пластины теплоизолированы, с одной поверхности пластины (при y = ly, ly – толщина пластины) происходит теплообмен со средой, а другая ее поверхность (y = 0) – теплоизолирована. Таким образом, уравнение одномерной теплопроводности вертикальной пластины с внутренним источником теплоты и указанными условиями на ее поверхностях, имеют вид [2, 3, 4]:
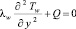, (7)
,
,
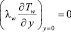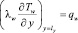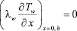, (8)
где qw – тепловой поток на границе раздела пластины и среды, qw = Q ly; lx = h – высота пластины.
Решением этих уравнений является одномерное температурное поле вертикальной пластины:
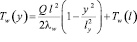, (9)
в котором Tw(l) представляет собой неизвестную пока температуру на границе раздела пластины (y = ly) и среды (y = 0) и которая определяется из решения сопряженной математической модели.
Температурное поле среды. Температурное поле в среде, пребывающей в состоянии свободной естественной конвекции с омываемой ею телом, определяется уравнениями (1)–(3), описывающими процесс взаимодействия между температурными полями тела и среды, возникающими в результате конвективных процессов, которые зависят сложным образом зависят не только от полей температуры, но и от векторного поля скоростей в каждой точке среды. Решения уравнений (1)–(3) имеют вид [3, 9] относительно безразмерных комплексов для температурного поля среды θ и координаты ξ
, 
,
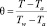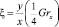где Grx – локальный безразмерный критерий Грасгофа [3].
Зависимости θ(ξ) для каждого значения критерия Pr с достаточной для практики точностью (не более 3 %) могут быть аппроксимированы многочленом второй степени (параболой). Для воздуха (Pr = 0,72) она может быть аппроксимирована параболой θ(ξ|Pr = 0,72) = 0,05(ξ – 4,5)2, откуда сразу же получается аналитическая формула для двумерного температурного поля среды T = T (x, y)
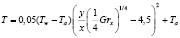. (10)
Решение задачи конвективного теплообмена в сопряженной постановке. Для получении искомого решения задачи сопряженного конвективного теплообмена приравняем на границе раздела пластины и среды тепловые потоки как со стороны среды (y = 0), так и со стороны пластины (y = ly). После несложных преобразований получим температурное поле среды T(x) на поверхности границы раздела между вертикальной пластиной и средой, вдоль оси x, которое установится в результате свободно конвективного теплообмена:
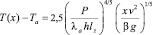. (11)
В последнем выражении введен полный тепловой поток Р внутреннего источника теплоты в теле, который связан с объемной плотность Q равенством P = Q h ly lz, где lz – длина пластины вдоль оси z. Установившееся в результате конвективного теплообмена с воздушной средой температурное поле вдоль границы раздела поверхность пластины – среда T (x) (11), приведено на рис. 1. Зависимость Tw – Ta построена для безразмерной координаты x/h вдоль вертикальной оси x, при следующих параметрах пластины и воздушной среды: Ta = 30 °С, P = 5 Вт, ρ = 1,165 кг/м3, λ = 0,026 Вт/мК, ν = 0,000016 м2/с, lx×ly×lz = = 0,16 м×0,002 м×0,2 м.
Из решения следует, что температурное поле в среде на границе раздела пластина – среда довольно сильно изменяется вдоль координаты x, даже при бесконечно большой теплопроводности пластины, при которой температура ее поверхности Tw постоянна. Поэтому замена температурных распределений их усредненными характеристиками, как в концепции КТО будет приводить к неадекватным результатам.
Сравним линейное уравнение Ньютона в концепции КТО с аналогичным приближением, но полученным на основании точного решения (11). Усреднив по высоте пластины h температуру поверхности границы раздела пластина – среда, после интегрирования (11) и несложных преобразований получим среднюю по высоте пластины температуру на границе раздела пластина – среда:
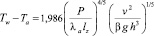. (12)
Отсюда получаем соотношение, связывающее тепловую мощность P внутренних источников теплоты в пластине с разностью температур поверхности пластины и окружающей ее средой Tw – Tа: в виде подобном закону Ньютона P = A(Tw – Tа)5/4,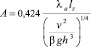 
.
Сравнение соотношений Ньютона и полученного решения показывает существенное отличие концепции КТО и линейного закона Ньютона от полученной модели (13), (14) конвективного теплообмена, так как по закону Ньютона тепловой поток Р должен быть прямо пропорционален Tw – Tа, в то время как (13), 14), он пропорционален (Tw – Tа)5/4.