За исключением квантовой жидкости гелия, теория жидкостей до сих пор остается до конца неразработанной. Наряду с этим, из полутеоретических и эмпирических соображений, а также с использованием разных моделей даны объяснения некоторым свойствам жидкостей и их зависимостям от внешних факторов. Более того, были определены аналитические функции этих зависимостей. В частности, температурная зависимость вязкости нормальных жидкостей описывается известным уравнением Френкеля-Эйринга [1, 5, 7]:
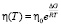. (1)
Здесь η0 – является величиной постоянной для данной жидкости и характеризует вязкость жидкости при бесконечно больших температурах, когда вся жидкость переходит в газообразное состояние. Величина этого параметра того же порядка, что и вязкость газов (10–4÷10–5 Ра∙сек), DG – свободная энергия активации вязкого течения жидкости. Формула Френкеля-Эйринга описывает температурную зависимость вязкости подавляющего большинства нормальных жидкостей с высокой степенью корреляции. Так, например, зависимость вязкости четыреххлористого углерода η от обратной температуры [2, 6], приведенная на рис. 1, очень хорошо описывается уравнением Френкеля-Эйринга (R2 = 0,9999).
Рис. 1. Зависимость вязкости четыреххлористого углерода от 1/Т
Рис. 2. Зависимость вязкости воды от обратной температуры
На рис. 2 представлена зависимость вязкости воды от температуры в координатах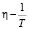 
[2, 6]. Как следует из рисунка, аналитическая кривая, выраженная формулой Френкеля-Эйринга, не описывает с достаточной точностью экспериментальные точки, которые отклоняются от теоретической кривой при сравнительно низких температурах. Естественно предположить, что причина такого отклонения связана с изменением свободной энергии активации вязкого течения (DG) с температурой в рассмотренном интервале температур (в теории Френкеля предполагается постоянство свободной энергии активации вязкого течения DG). При изменении температуры пространственная сетка водородных связей воды также изменяется: при увеличении температуры слабые водородные связи разрушаются, при уменьшении температуры, наоборот, их число увеличивается. В результате происходит систематическое отклонение экспериментальных точек от формулы Френкеля.
В начале 80-х годах ХХ столетия Уберрейтер [8] для более точного аналитического описания температурной зависимости вязкости воды и ряда водных растворов использовал эмпирическую формулу Вогеля:
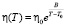. (2)
Уберрейтер исходил из соображений, что наличие водородных связей в водных растворах обуславливает большую скорость увеличения вязкости с понижением температуры, чем это происходит в бесструктурных жидкостях и как следует из выражения (2), бесконечно большое значение вязкости (η → ∞), соответствующее полному структурированию жидкости, имеет место не при абсолютной температуре Т = 0, а при более высоких температурах. Т0 – эта та самая низкая температура, при которой вязкость становится равной бесконечности. Как видно из рис. 3, график зависимости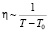 
, построенный для чистой воды, хорошо описывается уравнением (2) при значении Т0 = 146 К. Эту температуру Уберрейтер назвал структурной температурой.
Несмотря на то, что структурная температура по форме введения и численному значению является фиктивной величиной (параметром), она позволяет оценить влияние различных веществ, растворенных в воде, на структуру воды. Изучение изменения структурной температуры позволяет судить о структурных изменениях, происходящих в воде: увеличение значения структурной температуры свидетельствует о структурировании воды, уменьшение структурной температуры, наоборот, указывает на разрушение структуры воды [3, 4].
Как было отмечено выше, отклонение h(Т) от теории Френкеля-Эйринга связано зависимостью DG от температуры. Зависимость h(1/Т) для воды (рис. 2.) дает основание считать, что DG уменьшается с ростом температуры. В первом приближении эту зависимость можно представить в виде:
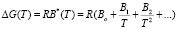. (3)
Ограничиваясь вторым членом соотношения (3) получим:
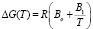. (4)
Ясно что, если температурная зависимость вязкости подчиняется уравнению Френкеля-Эйринга, то
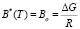. (5)
При бесконечно высоких температурах (Т → ∞) из-за отсутствия межмолекулярных взаимодействий энергия активации вязкого течения должна быть равна нулю и, следовательно, Во = 0. Тогда приняв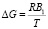 
, h(Т) можно представить в виде:
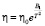. (6)
Если провести аппроксимацию экспериментальных данных согласно уравнению (6), то коэффициент корреляции достаточно высок и равен R2 = 0,9989 (рис. 4).
Рис. 3. Зависимость вязкости воды от 
Рис. 4. Зависимость вязкости воды от 1/Т2
Рис. 5. Зависимость вязкости воды от 1/Т2,72
Проведя оптимизацию по степени температуры, можно получить более высокое значение для коэффициента корреляции – при значении степени при температуре равной 2,72, величина достоверности оптимизации становится равной R2 = 0,9999 (рис. 5).
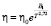. (7)
По всей вероятности, это связано с тем, что нельзя не учитывать вклад последующих членов ряда в формуле (3). Таким образом, температурная зависимость вязкости воды и водных растворов может быть описана предложенной нами формулой (7) и на основании этого могут быть найдены значения В1 и, соответственно, свободной энергии активации вязкого течения:
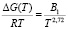(8)
и отсюда:
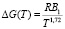. (9)
Как видно из соотношения (9) в отличие от теории, где предполагалось постоянство значения DG, свободная энергия активации вязкого течения является функцией температуры.
Рис. 6. Зависимость изменения свободной энергии активации вязкого течения водных растворов от изменения структурной температуры: Δ – водные растворы карбамида, ○ – водные растворы агарозы в присутствии бутилового спирта, ♦ – водные растворы агарозы
Например, при изменении температуры от 5 °С до 100 °С DG воды изменяется в пределах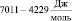 
.
При температуре Т = 300,15 K энергия активации вязкого течения для чистой воды равна: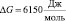 
. Вычисленные значения DG для водных растворов агарозы (полисахарид, который сильно структурирует воду) и карбамида (деструктурирует воду) при 300,15 K приведены в таблице. В таблице также приведены значения величин:
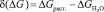(10)
и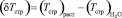 
. (11)
Свободная энергия активации вязкого течения и структурная температура воды и водных растворов
|
Вода |
Вода + карбамид моль/л |
Вода + агароза + 4 % бутиловый спирт вес. % |
Вода + агароза вес. % |
|||||||
|
1 |
2 |
3 |
5 |
0,04 |
0,08 |
0,10 |
0,10 |
0,12 |
||
|
DG, Дж/моль |
6150 |
5852 |
5740 |
5640 |
5579 |
6119 |
6780 |
6973 |
8127 |
9150 |
|
d(DG), Дж/моль |
– |
– 298 |
– 410 |
– 510 |
– 571 |
– 31 |
630 |
823 |
1977 |
3000 |
|
Tстр., К |
146 |
149 |
143 |
130 |
118 |
160 |
173 |
204 |
259 |
275 |
|
d Tстр., К |
– |
3 |
– 3 |
– 16 |
– 28 |
14 |
27 |
58 |
113 |
129 |
Как видно из соотношений (9) и (10) δ(DG) и δТстр являются, соответственно, изменениями свободной энергии активации вязкого течения (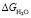
) и структурной температуры (
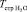) чистой воды при растворении в ней определенного количества вещества (DGраст и Тстр раст). Оба этих изменения должны быть связаны с изменениями структуры пространственной сетки водородных связей под влиянием введенного в воду вещества. Из сказанного следует, что должна существовать связь между изменением свободной энергии активации вязкого течения (δ(DG)) и изменением структурной температуры (δТстр) водных растворов. На рис. 6 представлена зависимость δ(DG) = f(δТстр) для некоторых водных растворов.
Наблюдаемая явная корреляция между указанными параметрами позволяет описать зависимость δ(DG) = f(δТстр) линейным уравнением, величина достоверности аппроксимации которого имеет вполне удовлетворительное значение (R2 = 0,9621).
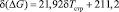. (12)
Таким образом, из зависимости вязкости водных растворов различных веществ от температуры с помощью предложенного нами соотношения (7) можно через изменения свободной энергии вязкого течения оценить структурную температуру водных растворов, а следовательно, и структурные изменения в водной фазе, что создаст возможность для классификации структурных изменений водных растворов по величине энергии активации вязкого течения.