Научные работы в сфере телекоммуникаций в основном посвящены исследованию информационных потоков, их статистических характеристик, и качественному выбору обоснованности математических моделей аналитического или имитационного характера. Необходимо учитывать, что в настоящее время есть много работ [1, 2, 3, 4] по исследованию трафика в IP-сетях, где каждому виду трафика сопоставлен закон распределения. Известно [1, 2, 3, 4], что наиболее широко применяются три вида распределений: Парето, Вейбулла и логнормальное, анализируя которые можно получить выражения для среднего времени задержки пакета в обрабатывающем устройстве и среднее время задержки пакета в сети [5, 6, 7, 8]. При этом при объединении потоков от однородных и разнородных источников трафика, сохраняется свойство самоподобия. Самоподобные процессы можно обнаружить по следующим равноценным признакам: медленно затухающая дисперсия, наличие долговременных зависимостей, наличие распределения с тяжелыми хвостами. Количественной оценкой степени самоподобия потока трафика является параметр Хёрста (от 0,5 до 1) [1, 9].
Цель исследования. Основной задачей исследования является поиск математических моделей самоподобных процессов, происходящих в мультисервисной телекоммуникационной сети, и методов определения параметров на разных узлах сети. Современные научные исследования передачи мультимедийных сообщений и оценки услуг предоставления трафика, неоднократно доказывают, что процессы, происходящие в сети, обладают неустойчивой структурой. Появление самоподобных свойств, задержек, не согласуемых с требованиями провайдера при передаче трафика, является основным вопросом, который требует решения.
Материалы и методы исследования
Как было сказано, интерес к поведению самоподобного и непрерывного трафика, особенно мультисервисной сети, является актуальной задачей. Существует несколько методов расчета показателей при данном стечении обстоятельств, но доказательств их применимости мало.
Многие исследователи стараются решить данную проблему с использованием классических методов. Например, с использованием классической теории Маркова, которая рассматривает предположения, что трафик описывается пуассоновскими распределениями. Однако доказано, что распределение трафика, описывающего самоподобные случайные процессы, отличается от пуассоновского, и превышает ожидаемые показатели качества обслуживания в несколько раз [1, 2, 3, 4]. Поэтому главной проблемой является то, что на практике не всегда удается согласовать результаты имитационного моделирования и экспериментальных наблюдений.
В данной статье мы рассматриваем вопрос описания трафика на примере частных случаев, а именно, нахождения его закона распределения, который наиболее точно показывает и приближает к его реальной структуре. При исследовании характеристик трафика использовались методы экспериментального наблюдения, анализа статистик с помощью программы-снифера WireShark.
Результаты исследования и их обсуждение
С целью исследования статистических характеристик мультимедийных потоков сети Internet, в том числе степени их самоподобия, анализировали три типа трафика:
• трафик Internet (передача данных);
• дополнительно с трафиком п. 1 добавляется трафик, формируемый просмотром видео-файла в режиме реального времени;
• дополнительно с трафиком п. 1 и 2 добавляется трафик IP-телефонии (Skype).
Все современные мультисервисные сети используют технологии, основанные на коммутации пакетов, в частности такие технологии, как АТМ и MPLS. Использование законов распределения длительности сообщений и времени их поступления на передачу позволяет оценить качество обслуживания трафика мультисервисной сети. Анализируя поступающие потоки трафика можно определить параметры функционирования обслуживающего устройства [9].
Для анализа класса распределений процессов поступления интервалов времени между пакетами и длительности пакетов была использована программа Easyfit Professional. Данный программный продукт позволяет произвести автоматическую селекцию класса статистических распределений.
В результате проведенных исследований трафика, были сопоставлены законы распределения, которые представлены в таблице.
При анализе трафика с помощью программы-снифера WireShark получаем статистические данные в форме текстовых файлов при измерении трафика. Затем выражаем по снятым статистическим данным реального потока, поступающего на вход сетевого элемента, параметры, такие как интервалы времени поступления пакетов, длины пакетов, и аппроксимируем их функции плотности распределения в виде гистограмм.
При аппроксимации снятых параметров трафика в программе Easyfit Professional получаем следующие законы распределения, представленные на рис. 1, 2, 3, 4, 5.
|
Тип трафика |
Уровень |
Закон распределения |
|
|
интервалы времени между пакетами |
длины пакетов |
||
|
Internet |
Канальный |
Парето |
Вейбулла |
|
VoIP |
Прикладной |
Парето |
Логнормальное |
|
IP |
Сетевой |
Парето |
Вейбулла |
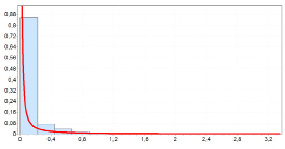
Рис. 1. Гистограмма измерений длительности поступления пакетов
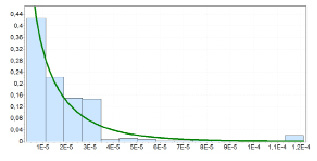
Рис. 2. Гистограмма измерений длительности обслуживания пакетов
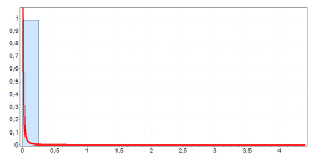
Рис. 3. Гистограмма измерений длительности поступления пакетов
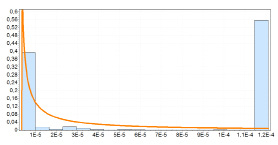
Рис. 4. Гистограмма измерений длительности обслуживания пакетов
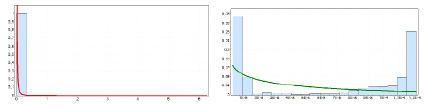
Рис. 5. Гистограмма измерений длительности поступления пакетов и длительности обслуживания пакетов
Следовательно, для первого случая интервалы времени между пакетами подчиняются закону распределения Парето с параметрами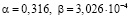 
(рис. 1), а длины пакетов – Вейбулла 
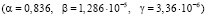(рис. 2).
Следовательно, для второго случая интервалы времени между пакетами подчиняются закону распределения Парето с параметрами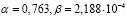 
(рис. 3)., а длины пакетов – логнормальному 
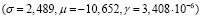(рис. 4).
Следовательно, для третьего случая интервалы времени между пакетами подчиняются закону распределения Парето с параметрами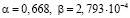 
, а длины пакетов – Вейбулла 
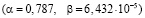(рис. 5).
Выводы
Большой практический интерес представляют оценки параметров трафика, передаваемого по каналам в период наибольшей нагрузки, которые зачастую невозможно определить. Поэтому, зная законы распределения, которым подчиняется реальный трафик, можно определить среднее время задержки пакета в сети, используя спектральный метод решения интегрального уравнения Линдли [7]. Следовательно, можно сделать вывод, что имитационное моделирование не имеет возможности подстраиваться под постоянно изменчивый характер трафика. Исследование и анализ его необходимо осуществлять средствами аналитических методов, алгоритмов, так как их применение позволяет наиболее точно оценить параметры сети.