Разработка программного обеспечения для работы на современных суперкомпьютерных системах, в силу усложнения алгоритмов обработки данных, делает задачу автоматизации одной из основных. Созданный программный комплекс предназначен для автоматического нахождения оптимальных наборов управляющих параметров весового метода конечных элементов (МКЭ) при решении краевых задач в областях с геометрией, содержащей критические точки (в которых решение становится сингулярным) с использованием возможностей вычислительного кластера.
Схема работы программного комплекса в нотации UML (рис. 1):
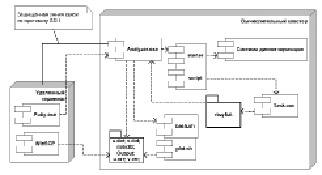
Рис. 1. Компоненты программного комплекса
В ходе разработки программного комплекса были реализованы следующие возможности:
– межплатформенное взаимодействие;
– автоматический захват свободных ресурсов кластера;
– вычисления штрафов – величин, характеризующих соответствие практической и теоретической скоростей сходимости весового МКЭ;
– процентное отношение количества узлов с абсолютной погрешностью не выше заданных предельных погрешностей;
– определение границ множества оптимальных степенейвесовой функции, при которой весовой МКЭ сходится со скорость не хуже теоретической;
– визуализация средствами кластера трехмерных поверхностей распределения абсолютной погрешности по каждой компоненте;
– автоматизация всех этапов работы программного комплекса.
Исходный код программы Analyzer.exe реализован на языке C++. Скрипты Starter и script написаны на языке командной оболочки Bash. Визуализация результатов выполняется при помощи скрипов написанных на языке командной оболочки Bash для интерактивного графопостроителя gnuplot.
При разработке программного комплекса широко использовались функции, предоставляемые стандартными библиотеками по работе с файлами и массивами данных, но большая часть алгоритмов не имеет аналогов по своему применению и была разработана нами полностью самостоятельно.
Программный комплекс прошел проверку нахождения оптимальных наборов управляющих параметров при исследовании двумерных задач теории упругости с сингулярностью, вызванной наличием на границе области входящего угла [1].
Начальные данные:
δ: 0.0-0.055 шаг 0.005
v: 2.3-2.75 шаг 0.05
v*: 0.0 -0.3 шаг 0.05
После первого этапа анализа были определены оптимальные наборы параметров, для которых построены графики распределения абсолютной погрешности (рис. 2-3):
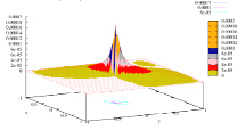
Рис. 2. График распределения абсолютной погрешности по компоненте u
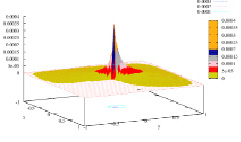
Рис. 3. График распределения абсолютной погрешности по компоненте v
Уточнённые диапазоны степени весовой функции: v[2.3,2.75] при δ=0.01, v*=0.2 и v[2.3,2.75] при δ=0.01, v*=0.25.
Использование программного комплекса позволяет значительно упростить работу по исследованию сингулярных задач. Следствием его применения на вычислительном кластере является более рациональное использование его ресурсов, а также экономия рабочего времени исследователя.

