Scientific journal

International Journal of Applied and fundamental research

ISSN 1996-3955

ИФ РИНЦ = 0,593

Применение математических методов является необходимым элементом современной экономики, не является исключением и оценочная деятельность, что подтверждает опыт оценщиков разных стран. Содержание и основная цель оценки – расчет наиболее вероятной цены объекта собственности на свободном конкурентном рынке. Методологической основой оценки являются три общепринятых подхода: сравнительный, доходный и затратный. С методологической точки зрения оценка определяется как научное направление прикладного экономического анализа, основанная задача которого состоит в установлении наиболее вероятной цены продажи или покупки актива на основе анализа динамики сил спроса на этот актив и его предложения на соответствующем сегменте рынка. Одним из направлений формализованного научного подхода является применение методов математики в оценке.

Использование математических методов в оценке предполагает следующую возможность их применения:

– в виде описательных математических моделей трех известных подходов и методов оценки, позволяющих лучше понять их сущность;

– в виде математических моделей результирующего показателя стоимости от множества ценообразующих факторов при использовании сравнительного подхода в оценке различных видов имущества [4].

Достоверная оценка стоимости необходима, в том числе для целей кредитования, страхования, вклада в уставный капитал, развития рынка ценных бумаг и т.д. Результаты недостоверной оценки залогового имущества наглядно продемонстрировал финансовый кризис 2008 года. Так, например, выборочная проверка выявила различие в стоимости одного и того же объекта, оцененного разными оценщиками. Возможными причинами подобных факторов является то, что наблюдался низкий уровень квалификации оценщиков, т.к. первоначально выдача лицензий производилась заочно на основании документов об образовании, без проведения квалификационного экзамена; в органах статистики не отслеживалась информация о ценах на различные виды имущества, показателях риска и внутренней нормы доходности различных категорий бизнеса, так как единый заказчик на эту информацию отсутствует.

Современная Концепция государственной политики в области оценки имущества направлена на поддержку оценочного сообщества и обеспечение проведения законной достоверной оценки [1]. Как известно между участниками рынка недвижимости всегда объективно существует конфликт интересов: продавец желает продать имущество как можно дороже, покупатель – купить как можно дешевле; арендодатель хотел бы, чтобы его имущество стоило дороже, а арендатор считает, что оно стоит более дешево, а значит и плата за аренду должна быть ниже; кредитор считает, что закладываемое имущество стоит дешевле, а кредитополучатель уверен, что стоимость отдаваемого в залог имущества велика, и т.п.

Разрешить данный конфликт интересов призван независимый оценщик, чья задача компетентно и беспристрастно оценить объект, аргументированно убедить участников трансакции в том, что рассчитанная им величина и есть та объективная стоимость, которая отражает ценность объекта на рынке в данный момент времени в данном месте. Таким образом, для аргументированного доказательства и достоверности оценки правомерно применение математически выверенных результатов стоимости. Для определения рыночной стоимости оцениваемой квартиры была построена регрессионная модель, описывающая взаимодействие основных ценообразующих факторов. Для этого, была собрана информация о цене предложений аналогичных квартир, расположенных в том же районе, что и объект оценки. Для построения регрессионной модели необходима оцифровка имеющейся информации по основным ценообразующим факторам. По мнению оценщика, таковыми являются: количество комнат, общая площадь, общая площадь кухни, этажность и занимаемый этаж, материал стен, тип квартиры, общее состояние квартиры. Месторасположение объектов аналогов не было выделено в качестве ценообразующего фактора, поскольку аналоги в выборке подобраны из типичного месторасположения с объектом оценки.

Следующим шагом является проверка наличия зависимости между каждой факторной переменной и результирующим показателем (цена предложения). Для оценки степени зависимости количественных переменных рассчитывался коэффициент корреляции. Расчет производился в среде MS Excel.

Таблица 1

Характеристика факторов в оцифровке

Таблица 2

Оцифровка информации по выборке

Полученные значения корреляции свидетельствуют о существовании ярко выраженной связи между общей площадью квартиры и ценой предложения, корреляция между количеством комнат и ценой предложения за 1 кв.м квартиры отсутствует, это связанно с тем, что для расчетов в качестве объектов аналогов была принята информация только по двухкомнатным квартирам [3].

Для ранговых факторов проверка значимости влияния производилась с помощью однофакторного дисперсионного анализа при расчете использовались встроенные возможности MS Excel («Сервис» → «Анализ данных» → «Однофакторный дисперсионный анализ»).

По итогам проверки можно сделать вывод о том, что приведенные в табл. 4. ценообразующие факторы не оказывают влияния удельную стоимость оцениваемой квартиры. В результате проверки тесноты, мы пришли к выводу, что на значение стоимости оказывают влияние только общая площадь. Для построения многофакторной регрессионной модели были выбраны общая площадь и стоимость за 1 кв.м. Определение параметров модели осуществлялось методом наименьших квадратов с помощью MS Excel («Сервис» → «Анализ данных» → «Регрессия»). Все параметры и показатели качества полученной модели представлены ниже.

Таблица 3

Корреляция количественных факторов

Таблица 4

Проверка значимости влияния качественных факторов

Таблица 5

Регрессионная статистика

Анализ показателей качества полученной модели: коэффициент детерминации R2=0,405, следовательно, полученная модель на 40,5% объясняет изменение стоимости под влиянием включенных в модель факторных переменных. Это высокое значение для данного показателя. Коэффициент детерминации всегда лежит в интервале от 0 до 1. Чем ближе значение коэффициента детерминации к единице, тем лучше модель описывает исходный ряд данных.Скорректированный коэффициент детерминации R2cкор=0,351, за счет поправки величина коэффициента детерминации существенно не уменьшилась, что подтверждает сделанный ранее вывод о хорошем качестве модели. F-критерий.

Таблица 6

Дисперсионный анализ

Таблица 7

Описание двухфакторной регрессионной модели

С помощью F-критерия проводится проверка значимости уравнения регрессии в целом. Эта процедура сводится к проверке статистической значимости коэффициента детерминации R2, то есть проверяется нулевая гипотеза R2=0. Эта гипотеза равносильна гипотезе β1 = β2 = … = βk = 0, F-критерий показывает следующее: если коэффициент R2 значим, следовательно, связь между y и факторными переменными действительно существует и можно приступать к ее объяснению. Если же коэффициент R2 незначим, то данные представляют собой набор не связанных между собой случайных чисел. Однако это еще не значит, что зависимости нет, возможно, просто исходных данных не достаточно для того, чтобы она проявилась. Если показатель значимости F меньше 0,05, то полученный результат является значимым. Если значимость F меньше 0,01, тогда полученный результат является высоко значимым. Если же значимость F больше 0,05, то модель является статистически незначимой. В нашем случае уровень значимости F-критерия составляет 0,019, так как данное значение существенно меньше 0,05, то полученная модель является значимой [4,5].

В итоге, после комплексного рассмотрения влияния на цену предложения 1 кв.м. объекта оценки 7-ми ценообразующих факторов, можно сделать вывод, что основной факторной переменной является общая площадь. Таким образом, модель сведена до однофакторной регрессии, в качестве факторной переменной – общая площадь, кв.м, зависимая переменная – цена предложения за 1 кв.м., тенге.

По имеющейся выборке был построен точечный график и описывающие зависимость функции средствами MS Excel. Как видно из представленного графика наибольшим коэффициентом детерминации обладает степенная зависимость (R2=0,436). Поэтому в качестве регрессионной модели была выбрана однофакторная степенная зависимость вида:

,

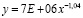где y – результирующая переменная (цена предложения, тенге/кв.м); 7Е+06 = 7·106; х – 1,04 – общая площадь объекта оценки в степени –1,04.

Коэффициент детерминации равен 0,436, что свидетельствует о статистической значимости построенной регрессионной модели. Произведем расчет стоимости объекта оценки с помощью выбранной однофакторной степенной зависимости:

7·106·43-1,04=140 052 тенге за 1 кв.м.

Таким образом, рыночная стоимость объекта оценки с использование метода математического моделирования составляет 140 052 × 43 = 6 022 236 тенге или округленно 6 022 000 тенге. В итоге применение регрессионной модели в оценке позволяет установить закономерность влияния основных ценообразующих факторов на изучаемый результирующий показатель, как в их совокупности, так и каждого фактора в отдельности. С помощью регрессионного анализа как метода математической статистики удается, во-первых, найти и описать форму аналитической зависимости результирующего показателя от факторных переменных и, во-вторых, оценить тесноту этой зависимости.