Одной из важных задач, возникающих при оптимизации различных технологических процессов является выявление условий или параметров, сдерживающих дальнейшую оптимизацию технологического режима, и установление областей более благоприятных значений этих параметров. Существующие методы, например, не пригодны для задач с базисной матрицей ограничений, близкой к вырожденной, характерных для задач с «возмущенными» или слабо различающимися между собой значениями параметров [5]. Само решение таких оптимизационных задач связано с проблемой неустойчивости полученных решений и рассматривалась многими исследователями [1, 6-9]. В частности, в предшествующих работах руководителя авторского коллектива предлагаемой статьи и его коллег [2-4] предложен метод решения оптимизационных задач распределения и размещения ресурсов между параллельными объектами с учетом возможной, но не обязательной вырожденности матриц ограничений, основанный на расширении множества допустимых значений этих задач.
1. Общая постановка задачи и структура имитационной модели
Пусть оптимальный технологический режим некоторого процесса определяется решением стандартной задачи математического программирования
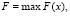 (1)
(1)
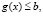 (2)
(2)
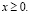 (3)
(3)
где х – n-мерный вектор, b – m-мерный вектор, g(x) – векторная функция.
Предполагается, что вектор правых частей ограничений (2) в течение заданного интервала времени (смена, сутки, декада и т.д.) может целенаправленно измениться на некоторую, в общем случае случайную, величину 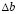 . Следовательно, необходимо разработать алгоритм для определения эффективных значений
. Следовательно, необходимо разработать алгоритм для определения эффективных значений 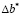 .
.
Общая структура имитационной модели для улучшения найденных ранее оптимальных режимов технологических процессов должна обеспечить выполнение следующих основных этапов.
1. Решение задачи описанной выражениями (1)-(3).
2. Моделирование возможных изменений параметров модели оптимизационной задачи [2].
3. Определение области изменений нестационарных параметров модели, приводящих к улучшению оптимального решения задачи (1)-(3).
В соответствии с приведенной структурой имитационной модели можно предложить следующий алгоритм поиска 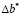 .
.
Шаг 1. Решение задачи (1)-(3).
Шаг 2. Вычисление значений 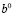 правых частей ограничения (2), соответствующих полученному оптимальному решению задачи (1)-(3). При условииповторного решения задачи (1)-(3) вычисление значения
правых частей ограничения (2), соответствующих полученному оптимальному решению задачи (1)-(3). При условииповторного решения задачи (1)-(3) вычисление значения 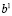 правых частей ограничения (2) и переход к шагу 6.
правых частей ограничения (2) и переход к шагу 6.
Шаг 3. Определение эффективных ограничений задачи.
Шаг 4. Моделирование 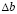 для эффективных ограничений.
для эффективных ограничений.
Шаг 5. Вычисление новых значений эффективных ограничений: 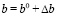 .
.
Шаг 6. Определение области изменения параметров задачи 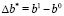 .
.
Шаг 7. Конец алгоритма.
Для задачи распределения ресурсов [3] в силу особенности её математической модели (наличие ограничения – равенства) процедура поиска оптимальных значений ∆b* может быть упрощена. Рассмотрим это на примере линейной и квадратичной задач распределения ресурсов.
2. Поиск оптимальных 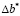 в задачах распределения ресурсов
в задачах распределения ресурсов
Рассмотрим задачу распределения ресурсов в линейной постановке:
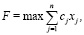 (4)
(4)
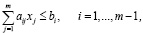 (5)
(5)
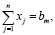 (6)
(6)
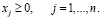 (7)
(7)
Здесь с учетом слабых различий параметров моделей параллельных процессов коэффициенты ограничений (5) могут быть представлены в виде: 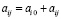 .
.
Распределение различных ресурсов, и в том числе, ресурсов, из которых формируются параллельные материальные или информационные потоки является одной из наиболее часто встречающихся проблем на практике.
Однако решение таких задач в большинстве случаев связано со значительными вычислительными проблемами.
Причина в том, что параллельные процессы обычно являются частично однотипными и это приводит к появлению малого параметра (эпсилон) в моделях этих задач и связанной с ним проблемы неустойчивости полученных решений из-за «плохой обусловленности» их матриц ограничений.
В статьях [3,4] авторов данной работы предложен метод решения оптимизационных задач распределения ресурсов между параллельными объектами с учетом возможной «плохой обусловленности» их матриц ограничений, основанный на расширении множества допустимых значений этих задач.
Суть этого подхода состоит в том, что решение исходной оптимизационной задачи (4-7) определяется путем направленного перехода к ее оптимальному решению из точки, соответствующей решению некоторой вспомогательной задачи (8)-(10) с расширенным множеством допустимых значений:
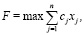 (8)
(8)
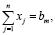 (9)
(9)
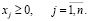 (10)
(10)
При этом вычислительная процедура становится не только нечувствительной к вырожденности матрицы ограничений задачи, но из-за специфики модели систем с параллельной структурой обеспечивает нахождение точного решения задачи.
Общая структура этапов решения задачи распределения ресурсов методом расширения имеет вид:
1. Решение расширенной задачи (8-10).
2. Проверка полученного решения на допустимость по ограничениям (5) исходной задачи. Если решение допустимо, то оно оптимально.
3. В противном случае переход к новому решению, для которого выполняются ограничения (5).
Обоснование и алгоритмы решения задачи (4)-(7) и приведенной ниже задачи с квадратичной целевой функцией (14)-(17) методом расширения приведены в статьях [3,4].
Установим, что в задаче (4)-(7) нестационарными параметрами являются ресурсы 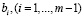 . Разложим целевую функцию (4) в ряд Тейлора в окрестности точки
. Разложим целевую функцию (4) в ряд Тейлора в окрестности точки 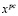 :
:
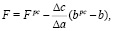 (11)
(11)
где 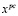 и
и 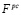 – соответственно, оптимальное решение и значение целевой функции расширенной задачи (12-14), полученные из исходной путем исключения «неудобных» ограничений (5) с возмущенными параметрами,
– соответственно, оптимальное решение и значение целевой функции расширенной задачи (12-14), полученные из исходной путем исключения «неудобных» ограничений (5) с возмущенными параметрами, 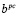 – значения правых частей ограничений (5), соответствующие решению
– значения правых частей ограничений (5), соответствующие решению 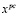
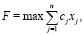 (12)
(12)
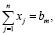 (13)
(13)
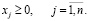 (14)
(14)
Установим связь между множествами решений 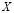 и
и 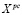 соответственно исходной и расширенной задач. Предположим, что исходная задача имеет единственное решение.
соответственно исходной и расширенной задач. Предположим, что исходная задача имеет единственное решение.
Очевидным является лемма 1 [3]: «Допустимое множество решений 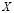 исходной задачи (4)-(7) всегда является подмножеством множества решений расширенной задачи (12)-(14), т.е.
исходной задачи (4)-(7) всегда является подмножеством множества решений расширенной задачи (12)-(14), т.е. 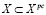 ».
».
Однако их оптимальные решения совпадут при выполнении условий следующей леммы 2 [3]: «Оптимальное решение исходной задачи совпадает с оптимальным решением расширенной задачи только тогда, когда:
1. Множества допустимых решений этих задач эквивалентны;
2. Оптимальное решение расширенной задачи принадлежит множеству 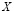 , т.е.
, т.е. 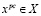 ». Доказательство приведено в [3].
». Доказательство приведено в [3].
Суть метода расширения [3,4] состоит в том, что решение исходной задачи (4)-(7) получается путем направленного перехода к ее оптимальному решению из точки, соответствующей решению расширенной задачи (12)-(14).
Поскольку анализ модели задачи (4)-(7) на чувствительность производится относительно ресурсов, то параметры 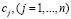 и
и 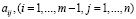 а также
а также 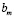 предполагаются постоянными. Следовательно, постоянными будут и величины
предполагаются постоянными. Следовательно, постоянными будут и величины 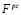 и
и 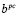 . Это, в свою очередь, приводит к линейной зависимости значения целевой функции от вектора b (см. рис. 1). Здесь
. Это, в свою очередь, приводит к линейной зависимости значения целевой функции от вектора b (см. рис. 1). Здесь 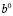 – вектор правых частей ограничений (5), соответствующий оптимальному решению задачи (4)-(7).
– вектор правых частей ограничений (5), соответствующий оптимальному решению задачи (4)-(7).
Из рис. 1 видно, что областью изменения ресурса b, в которой возможно улучшение найденного решения, является интервал 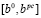 , т.е. при выборе нового значения b не должно нарушаться условие
, т.е. при выборе нового значения b не должно нарушаться условие
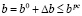 . (15)
. (15)
Очевидно, что условие справедливо и для каждой эффективной составляющей вектора b:
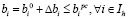 (16)
(16)
где 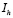 – множество индексов эффективных ограничений.
– множество индексов эффективных ограничений.
Для квадратичной задачи распределения ресурсов вида:
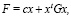 (17)
(17)
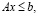 (18)
(18)
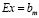 (19)
(19)
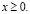 (20)
(20)
Вышеприведенные рассуждения также останутся справедливыми за исключением того, что зависимость F(b) примет нелинейный вид (рис. 2):
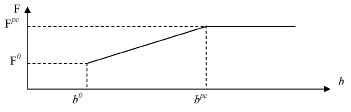
Рис. 1. Область изменения ресурса для линейной задачи
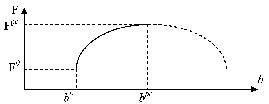
Рис. 2. Область изменения ресурса для нелинейной задачи
Специфика математической модели задач распределения ресурсов позволяет не только найти оптимальное значение (b) дефицитного ресурса, как это было сделано выше, но и установить взаимное влияние между собой нескольких дефицитных ресурсов.
3. Алгоритм поиска оптимальных 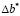 в задачах распределения ресурсов
в задачах распределения ресурсов
Алгоритм состоит из следующих шагов.
Шаг 1. Решение расширенной задачи (12)-(14).
Шаг 2. Переход к решению исходной задачи распределения ресурсов.
Шаг 3. Определение эффективных ограничений задачи. Если эффективное ограничение одно, то определение области изменения параметров по формуле: 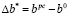 . Процесс вычислений на этом заканчивается, на шаг 6. Если же эффективных ограничений несколько, то переход к следующему шагу.
. Процесс вычислений на этом заканчивается, на шаг 6. Если же эффективных ограничений несколько, то переход к следующему шагу.
Шаг 4. Изменение основного ресурса в пределах: 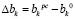 .
.
Шаг 5. Вычисление новых значений остальных ресурсов по формуле (21), на шаг 4.
Шаг 6. Конец алгоритма.
Заключение
Результаты работы были использованы при разработке информационной системы крупной компании по хранению, переработке и реализации зерна «Цесна-Астык», характеризующейся разветвленной последовательно-параллельной технологической структурой, где на каждом технологическом этапе переработка зерна осуществляется на нескольких параллельно включенных агрегатах со слабо отличающимися характеристиками. Поэтому при построении моделей этапов переработки была получена система уравнений с малыми параметрами. Экспериментальная реализация имитационного анализа эффективных значений нестационарных параметров данного производства на основе компьютерной имитации характеристик производственного процесса позволила выявить дополнительные производственные ресурсы и увеличить производственные мощности до 5,0%. Численная реализация задачи распределения ресурсов в процессе имитационного анализа также показала эффективность использованного для ее решения метода расширения допустимых значений [3,4] для моделей с малыми параметрами.

