Scientific journal

International Journal of Applied and fundamental research

ISSN 1996-3955

ИФ РИНЦ = 0,593

Транспортная задача, как и задача линейного программирования была впервые поставлена советским экономистом А.Н. Толстым в 1930 году. Разработка общих методов решения задачи линейного программирования и их математическое исследование связано с именем советского ученого Л.В. Канторовича. В 1939 году методам решения задачи линейного программирования посвящено также большое число работ зарубежных ученых. Основной метод решения задачи линейного программирования – симплекс метод – был опубликован в 1949 году Дандигом. Симплекс метод дает решение любой задачи линейного программирования, но если переменных очень много, то решение весьма затруднительно и для более сложных задач симплекс метод стали модифицировать [1].

Цель исследования. Целью работы является установление методики решения транспортно-складской задачи для механизации строительного производства и организации технологических процессов протяженного объекта.

Идея работы заключается в создании комплекса, позволяющего произвести расчет эффективной организации строительного производства по различным критериям (себестоимость работ, производительность и т.д.) на базе существующих методик решения транспортной и складской задач.

Материалы и методы исследования

Транспортная задача делится на два вида: транспортная задача по критерию стоимости – определение плана перевозок, при котором стоимость груза была бы минимальна; транспортная задача по критерию времени – более важным является выигрыш по времени [2].

Для каждого из пунктов производства задан объем производства, а для каждого пункта потребления – объем потребления. Известна стоимость перевозки из каждого пункта производства в каждый пункт потребления единицы продукта. Требуется составить план перевозок продукта, в котором все пункты потребления были бы обеспечены необходимыми продуктами, ни из какого пункта производства не вывозилось бы продуктов больше, чем там производится, а стоимость перевозки была бы минимальной.

Пусть имеется n поставщиков – строительные материалы разной продукции (присвоим им имена – ai) и m потребители – строительные бригады этой продукции (bj). Каждый поставщик может поставлять свою продукцию любому из потребителей. Известны затраты Cij на перевозку единицы продукции от каждого поставщика к каждому потребителю. Необходимо так распределить перевозки, чтобы суммарные затраты были минимальными. Элементы решения – Хij количество продукции, перевозимой от каждого поставщика к каждому потребителю [3]. Требуется составить план перевозок груза, в котором все пункты потребления были бы обеспечены необходимыми строительными материалами, ни из какого пункта производства не вывозилось бы грузов больше, чем там производится, а стоимость перевозки была бы минимальной.

Структурная схема транспортной задачи при строительстве автомобильных дорог приведена в графической постановке на рис. 1.

При этом будем иметь в виду, что строительные бригады – потребителм материалов, не закреплены в пространстве, а постоянно перемещаются вдоль объекта строительства.

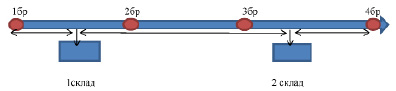
Рис. 1. Пример структурной схемы транспортной задачи

Обозначим через Ai возможности поставщиков, основных складов и через Bj строительные бригады потребности которых является строительные материалы.

Составим математическую модель задачи.

Ограничения по производственным мощностям поставщиков:

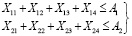(1.1)

Ограничения по производственным мощностям потребителей, строительных бригад:

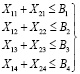(1.2)

Целевая функция – требование минимизации суммарных затрат на перевозки:

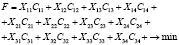. (1.3)

В краткой форме записи эта модель для связи потребителей и поставщиков имеет вид:

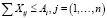(1.4)

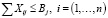; (1.5)

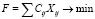. (1.6)

Закрытой моделью транспортной задачи называется такая задача, в которой суммарные потребности потребителей равны суммарным возможностям поставщиков, то есть

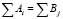. (1.7)

Построим исходный опорный план. Опорный план является основой для оптимизации процесса. Существует несколько способов его построения. Здесь описано два из них. Один из них – метод северо-западного угла – наиболее простой, но и наименее эффективен, второй – метод наименьшего элемента несколько сложнее, но значительно ближе к оптимальному [4].

Метод северо-западного угла. Существует несколько методов составления исходного опорного плана. Самый простой из них – метод «северо-западного угла». Исходные данные примера (затраты на перевозку единицы продукции от каждого поставщика к каждому потребителю) приведены в верхних правых углах табл. 1.

Таблица 1

Опорный план решения транспортной задачи, составленный методом «северо-западного угла»

* в скобках даны значения начального момент времени.

При каждой случаи строительных бригад, по мере придвижение вдоль строящегося дороги на каждые 8 часов работы расчет будет повторятся.

Метод наименьшего элемента состоит в заполнении клеток, начиная с тех, в которых стоят наименьшие затраты на перевозку (см. табл. 1.2) [5]. В данном случае минимальную стоимость имеют перевозки по каналу А₁-В₄ – 65 т. Ставим в эту клетку максимально возможное количество перевозок – 110 (т.к. возможности А1=110). Следующие по затратам на перевозку каналы А₁-В₂ и А₁-В₁. Однако, возможности А₁ уже исчерпаны, поэтому далее заполняется клетка, соответствующая каналу А₂-В₃, в которую ставим 80 единицы груза (А₂=150). Далее заполняем клетку А₂-В₄. Сюда можно поставить только 65, т.к. четвертому потребителю требуется 65, а он уже получает от А₁.

Следующие по затратам перевозки по каналу А₁-В₂ – 45 т. В эту клетку можно поставить только 45 единиц груза, т.к. А₁=110, а он уже поставил 65 единиц груза потребителю В₄, по минимальной себестоимости.

Канал А₂-В₄ мен А₁-В₃ пен А₁-В₁ не рассматриваем, т.к. возможности А₂ уже исчерпаны, а потребности В₄ полностью удовлетворены. Поэтому затем заполняется клетка, соответствующая каналу А₂-В₂ (затраты на перевозку – 150 т.)

В дальнейшем транспортная таблица заполняется аналогично.

Предположим, что строительные бригады переместились на 15 километров от первоначальной точки строительства вдоль строящейся дороги. Исходная транспортная таблица задачи с изменением местоположения строительных бригад и складов будет составлена методом наименьшего элемента.

В распределении перевозок учитывается растояние от поставщика до потребителя, и считается себестоимость этих поставок. По наименьшей себестоимости будет распределен груз для ближайших пунктов потребления.

Таблица 2

Решения транспортной задачи составленный методом «северо-западного угла» по себестоимости и по оптимальной доставке груза

Таблица 3

Транспортная задача составленная методом «наименьшего элемента», после изменение потока строительных бригад

Таблица 4

Транспортная задача составленная методом «наименьшего элемента» для нахождения оптимальной доставки груза по минимальной себестоимости, после передвижения потока строительных бригад на 15 километров

Результаты исследования и их обсуждение

Установлено методика решения транспортно-складской задачи для механизации строительного производства и организации технологических процессов строительных предприятий. На основе решения транспортной задачи на примере строительства протяженных объектов была разработана методологическая основа построения эффективных транспортно – складских систем в динамичных условиях строительных технологических процессов.

Введение переменных координат местоположения, как потребителей, так и поставщиков товаров, показывает что организация строительства протяженных объектов может быть оптимизирована по сокращению транспортных расходов на доставку всех строительных материалов.

На приведенных примерах показано, как осуществляется расчет транспортно-складской задачи при учете перемещения потребителей и поставщиков товаров в пространстве. При этом производилась постоянная проверка определения себестоимости перевозок от различных поставщиков.

Выводы

Таким образом, расчет будет производиться до тех пор, пока все строительные бригады не осуществлят полное перемещение вдоль строящейся дороги. При необходимости расчет можно производить через каждые 8 часов рабочей смены строительных бригад. Используя расчет складской задачи с переменным расположением складов можно добиться оптимального размещения строительных материалов по мере производства работ. Данная методика позволит рационально распределить материалы, которые необходимы строительным бригадам, по всей длине строящегося объекта.