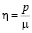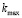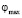В настоящее время поиск аналитических решений задач нелинейной теории упругости является достаточно сложной задачей. Одной из сложностей при построении математических моделей таких задач является учет несжимаемости материала. Условие несжимаемости несет дополнительную информацию о геометрии деформирования. В работе [1] предложена приближенная математическая модель нелинейной теории упругости для плоской деформации однородного изотропного материала, в рамках которой условие несжимаемости выполняется автоматически. В качестве метода построения приближенной модели плоской деформации используется метод возмущений, использующий разложения по степеням малого параметра объекты, описывающие напряженно-деформированное состояние. Однако из-за громоздких вычислений разложение выше второго порядка практически не используется. Появление современных пакетов символьной математики позволяет написать программы, облегчающие манипулирование с громоздкими выражениями, описывающими эффекты второго порядка при произвольном напряженно-деформированном состоянии. Эти эффекты выделяются при ограничении разложений для радиус-вектора частиц в текущей конфигурации 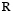 и функции гидростатического давления p членами до второго порядка по малому параметру
и функции гидростатического давления p членами до второго порядка по малому параметру 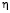 .
.
Математическая постановка задачи
В рамках рассматриваемой модели можно ограничиться выражением для потенциала энергии деформации в форме, предложенной в [2]:
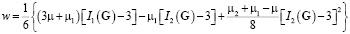 ,
,
где m, µ1 и µ2 – константы, причем m – модуль сдвига линейной теории, 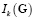 – главные инварианты меры деформации Коши G.
– главные инварианты меры деформации Коши G.
Следуя работе [3], разложение радиус-вектора точек в плоскости, ортогональной оси OZ, в текущей конфигурации представляется в виде
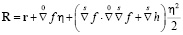 . (1)
. (1)
Здесь r – радиус-вектор точек в отсчетной конфигурации, 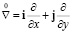 – оператор Гамильтона в базисе исходной конфигурации,
– оператор Гамильтона в базисе исходной конфигурации, 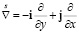 – симплектический оператор. Дифференциальные операторы действуют только на первый множитель справа, не являющийся оператором. Точка означает скалярное произведение.
– симплектический оператор. Дифференциальные операторы действуют только на первый множитель справа, не являющийся оператором. Точка означает скалярное произведение.
Используя разложение (1), получим представления в рамках эффектов второго порядка тензора напряжений Коши
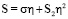 , (2)
, (2)
где 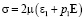 ,
, 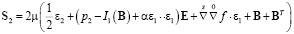 ,
,
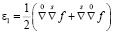 ,
, 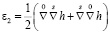 ,
, 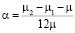 ,
,
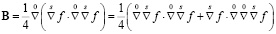 ,
,
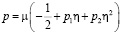 – функция, связанная с гидростатическим давлением, знак «Т» – транспонирование.
– функция, связанная с гидростатическим давлением, знак «Т» – транспонирование.
Уравнения равновесия приводятся к системам дифференциальных уравнений для эффектов первого и второго порядков соответственно:
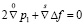 ,
,
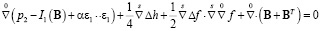 , (3)
, (3)
Условие интегрируемости системы уравнений (3) для эффектов первого, второго и третьего порядков соответственно приводит к дифференциальным уравнениям:
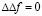 ,
, 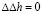 .
.
Обозначим 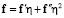 – разложение вектора плотности внешних сил, приложенного к деформированной боковой поверхности и рассчитанного на единицу площади этой поверхности. Тогда силовые граничные условия в напряжениях запишутся в виде
– разложение вектора плотности внешних сил, приложенного к деформированной боковой поверхности и рассчитанного на единицу площади этой поверхности. Тогда силовые граничные условия в напряжениях запишутся в виде
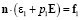 ,
,
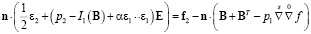 , (5)
, (5)
где 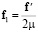 ,
, 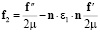 .
.
Если плотность внешних сил 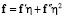 задана в отсчетной конфигурации, а нагружение «мертвое», то
задана в отсчетной конфигурации, а нагружение «мертвое», то 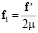 ,
, 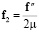 .
.
Выражения (1) – (5) представляют постановку граничной задачи нелинейной теории упругости. Так как уравнения (4) для эффектов первого и второго порядков приводят к бигармоническим уравнениям относительно искомых функций 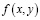 и
и 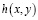 , то поиск аналитического решения краевых задач для эффектов первого и второго порядка можно проводить единым образом в автоматическом режиме.
, то поиск аналитического решения краевых задач для эффектов первого и второго порядка можно проводить единым образом в автоматическом режиме.
С помощью стандартной процедуры [4] граничные задачи линейной теории упругости для эффектов первого и второго порядков сводятся к интегральным уравнениям теории функций комплексной переменной. Рассматриваются только области, которые можно конформно отобразить на внешность окружности единичного радиуса с центром в начале координат с помощью функции вида
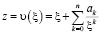 ,
,
где 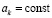 .
.
Для этих областей интегральные уравнения теории функций комплексной переменной приводятся к алгебраическим уравнениям с помощью интегралов типа Коши.
Перейдем к комплексным переменным 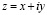 ,
, 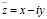 и введем комплексные потенциалы по формуле Гурса:
и введем комплексные потенциалы по формуле Гурса:
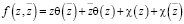 ,
,
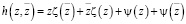 .
.
Для данных потенциалов уравнения (4) выполняются тождественно, а решением системы уравнений равновесия (3) являются функции:
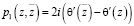 ,
,
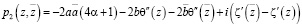 ,
,
где
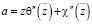 ,
, 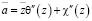 ,
, 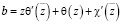 ,
, 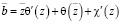 .
.
Искомые потенциалы аппроксимируются разложением в ряды Лорана, а коэффициенты находятся из условия удовлетворения граничным условиям (5) на бесконечности и на контуре отверстия. На бесконечности с помощью предельного перехода получаем конечную систему линейных алгебраических уравнений для части коэффициентов разложения. Получение уравнений для оставшихся коэффициентов требует вычисления интегралов типа Коши на контуре отверстия. Т.к. на свободном от нагрузки контуре нормальные напряжения равны нулю, то тангенциальные напряжения на контуре, потребные для вычисления коэффициента концентрации, вычисляются в виде инварианта тензора напряжений Коши
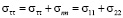 и
и 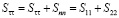
для эффектов первого и второго порядков соответственно.
Для нахождения аналитического решения задач о концентрации напряжений около отверстий на базе пакета символьной математики Maple создан комплекс программ, позволяющий автоматизировать символьные вычисления. Все операции распространены на тензоры до второго порядка включительно, компоненты которых являются рядами по малому параметру. Алгоритм позволяет находить выражение коэффициента концентрации напряжений для различных форм отверстия при различных видах деформации в рамках эффектов второго порядка.
Задача о концентрации напряжений около квадратного отверстия при равномерном растяжении на бесконечности
Без потери общности будем считать радиус отверстия равным единице. Контур отверстия свободен от напряжений. На бесконечности приложена равномерная радиальная нагрузка интенсивности p, Н/м2. Универсальным силовым параметром, имеющим ту же размерность, является модуль сдвига линейной теории упругости 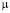 . Поэтому естественно возникает безразмерный малый параметр вида
. Поэтому естественно возникает безразмерный малый параметр вида 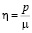 .
.
В цилиндрической системе координат 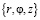 введем единичный базис
введем единичный базис 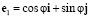 ,
, 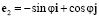 ,
, 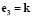 . Коэффициент концентрации напряжений в нелинейной теории, как и в классическом решении линейной теории, будем определять как
. Коэффициент концентрации напряжений в нелинейной теории, как и в классическом решении линейной теории, будем определять как
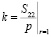 ,
,
где 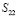 – тангенциальная компонента «плоской» части тензора истинных напряжений Коши
– тангенциальная компонента «плоской» части тензора истинных напряжений Коши 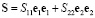 . Представление этой компоненты в рамках приближенной теории имеет вид
. Представление этой компоненты в рамках приближенной теории имеет вид 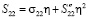 , откуда, вспоминая, что
, откуда, вспоминая, что 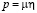 , получим выражение для коэффициента концентрации в рамках приближенной теории:
, получим выражение для коэффициента концентрации в рамках приближенной теории:
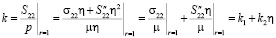 .
.
Конформное отображение внешности квадрата на внешность круга 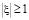 задается формулой
задается формулой 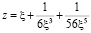 . Вершинам квадратного контура соответствуют значения полярного угла
. Вершинам квадратного контура соответствуют значения полярного угла 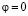 ,
, 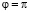 и
и 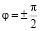 . На бесконечности приложена равномерная нагрузка интенсивности
. На бесконечности приложена равномерная нагрузка интенсивности 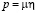 , где
, где 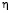 – малый параметр. Тогда на бесконечности вектор внешних сил
– малый параметр. Тогда на бесконечности вектор внешних сил 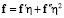 на площадках с нормальным вектором
на площадках с нормальным вектором 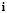 имеет разложение
имеет разложение 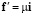 ,
, 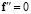 , а на площадке с нормальным вектором
, а на площадке с нормальным вектором 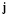 разложение –
разложение – 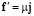 ,
, 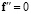 .
.
Для квадратичного приближения разложение коэффициента концентрации напряжений по малому параметру 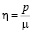 в вершинах квадратного отверстия принимает вид
в вершинах квадратного отверстия принимает вид 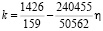 . Таким образом, наблюдаем уменьшение значения тангенциальных напряжений с увеличением величины интенсивности приложенной внешней нагрузки
. Таким образом, наблюдаем уменьшение значения тангенциальных напряжений с увеличением величины интенсивности приложенной внешней нагрузки 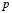 . Графики распределения относительных тангенциальных напряжений на внутреннем контуре отверстия, свободном от нагрузок, вычисленных в рамках эффектов первого и второго порядков при различных значениях параметра
. Графики распределения относительных тангенциальных напряжений на внутреннем контуре отверстия, свободном от нагрузок, вычисленных в рамках эффектов первого и второго порядков при различных значениях параметра 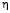 , изображены на рис. 1 и 2.
, изображены на рис. 1 и 2.
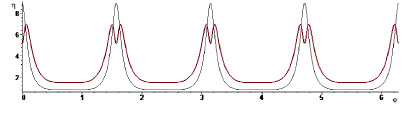
Рис. 1. Распределение относительных тангенциальных напряжений на контуре отверстия (развертка) при 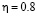 . Тонкая линия соответствует решению в рамках линейной теории, толстая линия соответствует квадратичному решению
. Тонкая линия соответствует решению в рамках линейной теории, толстая линия соответствует квадратичному решению
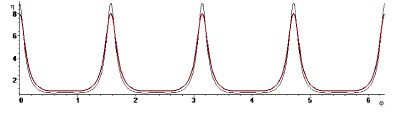
Рис. 2. Распределение относительных тангенциальных напряжений на контуре отверстия (развертка) при 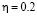 . Тонкая линия соответствует решению в рамках линейной теории, толстая линия соответствует квадратичному решению
. Тонкая линия соответствует решению в рамках линейной теории, толстая линия соответствует квадратичному решению
Как видно из графиков, в квадратичном приближении при различных значениях параметра 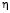 максимум величины коэффициента концентрации напряжений k достигается при различных значениях j, при этом его величина, по сравнению с классическим решением линейной теории, уменьшается. Заметим, что при учете внешней нагрузки p в разложении коэффициента концентрации напряжений наблюдаем эффект раздвоения одного максимума в вершине угловой точки на два симметричных максимума в окрестности данной вершины. При этом в самой вершине достигается минимум.
максимум величины коэффициента концентрации напряжений k достигается при различных значениях j, при этом его величина, по сравнению с классическим решением линейной теории, уменьшается. Заметим, что при учете внешней нагрузки p в разложении коэффициента концентрации напряжений наблюдаем эффект раздвоения одного максимума в вершине угловой точки на два симметричных максимума в окрестности данной вершины. При этом в самой вершине достигается минимум.
Исследовав функцию 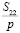 на экстремум, получаем, что значениям
на экстремум, получаем, что значениям
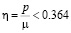
соответствует один экстремум: максимум достигается в вершинах квадратного контура. При 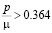 каждому значению
каждому значению 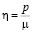 соответствует три точки экстремума: в вершинах квадрата достигается минимум, а двум другим корням производной
соответствует три точки экстремума: в вершинах квадрата достигается минимум, а двум другим корням производной 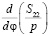 соответствуют максимумы.
соответствуют максимумы.
Максимальные значения коэффициента концентрации напряжений 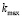 , вычисленные с точностью 10–6, и соответствующие им значения полярного угла
, вычисленные с точностью 10–6, и соответствующие им значения полярного угла 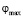 в зависимости от величины малого параметра h записаны в таблице.
в зависимости от величины малого параметра h записаны в таблице.
Экстремальные значения коэффициента концентрации 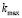 и соответствующие им значения полярного угла
и соответствующие им значения полярного угла 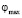
|
|
|
|
|
0.1 |
8.4929885 |
0 |
|
0.2 |
8.0174237 |
0 |
|
0.3 |
7.5418589 |
0 |
|
0.364 |
7.2374980 |
0.0031250 |
|
0.4 |
7.0911554 |
0.0236328 |
|
0.5 |
6.8714057 |
0.0437500 |
|
0.6 |
6.8041820 |
0.0500000 |
|
0.7 |
6.8603106 |
0.0633789 |
|
0.8 |
6.9618454 |
0.0696289 |
|
0.9 |
7.1029659 |
0.0750000 |
Выводы
Построенная приближенная математическая модель позволяет находить аналитическое решение плоских задач нелинейной теории упругости о концентрации напряжений около отверстий на базе математического пакета Maple.
Алгоритм применен для решения задачи о концентрации напряжений около квадратного отверстия при равномерном растяжении на бесконечности. Показано, что учет нелинейности в области концентраторов напряжений не только снижает значение тангенциальных напряжений, но и позволяет говорить об эффекте раздвоения одного максимума в вершине угловой точки на два симметричных максимума в окрестности данной вершины.