Кыргызстан – горная страна с большим количеством рек и значительным водным балансом. Широкое распространение для выработки электроэнергии в удалённых районах получают гидроэлектростанции – малой мощности, в силу экономичности получения, доступности и большего объема гидроэнергетического потенциала малых рек. Подавляющее большинство энергоустройств для выработки электричества используют в качестве гидродвигателя турбину, и лишь малая часть – водяные колеса.
Это обьясняется тем что, гидротурбины, выпускаются производством, широко распространены и имеют преимущество в скорости вращения, надёжности и технологичности производства, хотя требуют большого напора и скорости проходящей через них воды, что ограничивает область их применения полноводными реками и водохранилищами, сохраняющие, относительно, водный баланс круглый год. А водяные колеса используются в основном в качестве насоса для поднятия воды, в реках сельскохозяйственного назначеня с малым напором и скоростью.
Причины малого распространения водяных колёс – низкая частота вращения, большие габариты и сложность отбора механической энергии. В то же время простота их конструкции, доступное обслуживание, удобство в эксплуатации, низкие затраты на обустройство каналов для установки, высокая эффективность при низких напорах и малых скоростях, что широко распространено в сельских зонах (равнинных частях) Кыргызстана делает его привлекательным для использования в качестве гидродвигателя [1, 2].
По своему устройству на водные потоки водяные колеса делятся на вертикальные и горизонтальные; по использованию водной энергии – на напорные и безнапорные, по приему водного потока – верхнебойные, среднебойные и нижнебойные. Конструкцию водяного колеса условно можно разделить на три части:
1) Ось;
2) Опора (балки) для крепления лопастей, закрепленная на оси;
3) Лопасти. Обычно их КПД (всех типов) составляет в пределах 0,3–0,8 [3].
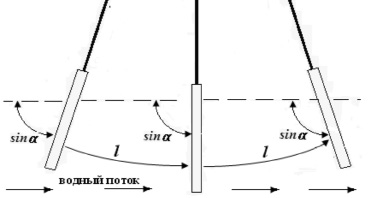
Рис. 1. Движение лопасти в водном потоке
Так как непосредственно передача энергии осуществляется через систему лопасть – опора – ось, то и эффективность водяного колеса зависит от их конструкции. В данном случае мы рассмотрим процесс передачи энергии (потенциальной и кинетической) водного потока к лопасти – вход лопасти в водный поток и силы, действующие на него со стороны потока и противодействующие ему. При расчете лопасти принимаются как удлиненные четырехугольники с прямыми сторонами.
Водный поток давит на лопасть перпендикулярно его плоскости, и угол между потоком воды и лопастью составляет 90°, когда лопасть полностью или максимально возможно погружена в водный поток [4]. В этот момент времени происходит максимальный переход энергии водного потока на лопасть, что мы собираемся показать математическим путем для единичной лопасти, погруженной в водный поток. На рис. 1 водный поток ударяется о площадь лопасти, погруженную в воду, и обтекает её. В этот момент времени водный поток совершает работу, сдвигая лопасть на определенное расстояние. Это расстояние определяет вращающий момент центральной оси водяного колеса. Кроме того, показан угол атаки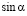 
на лопасть водным потоком. Из совокупности факторов (масса, скорость и угол атаки) изменяется полезная работа или сила единичной лопасти, что рассмотрим ниже.
Начнем с того, что совершаемая работа водного потока по вращению водяного колеса получается изменением кинетической энергии:
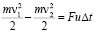, (1)
где m – масса воды, действующая на лопасть за время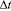 
, кг;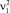 
– начальная скорость потока воды, м/с; 
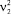– конечная скорость потока воды, м/с; F – сила, приводящая в движение водяное колесо с линейной скоростью u, H.
Изменение скорости потока воды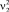 
равняется линейной скорости водяного колеса u. Тогда
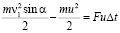, (2)
откуда
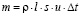, (3)
где ρ – плотность воды, кг/м3; l – глубина погружения лопасти, м; s – его поперечное сечение, м2; u – скорость входящего водного потока; ∆t – время скорости водяного колеса, с;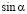 
– угол атаки лопасти к направлению потока воды.
Подставив (2) в формулу (3), получим:
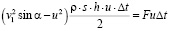. (4)
Сократим время ∆t и линейную скорость u в обеих сторонах равенства (4), тогда выражение примет вид:
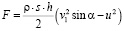. (5)
Данное выражение характеризует полезную силу единичной лопасти водяного колеса, передаваемую через вал на генератор.
Теперь рассмотрим эту силу с точки зрения скорости водяного колеса. Из уравнения (5) сила будет равна:
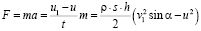, (6)
где, используя (3) получим:
.
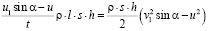Сокращая одинаковые значения, получаем:
.
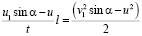Приравнивая его к расстоянию l, пройденному лопастью за время t:
.
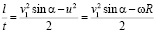Откуда,
;
;
,
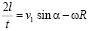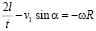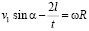где ω – угловая скорость, об/с; R – радиус водяного колеса, м.
Преобразовывая, получаем угловую скорость:
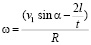. (7)
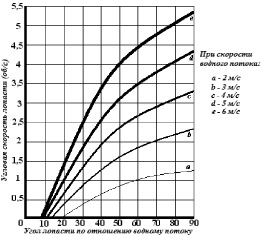
Рис. 2. Зависимость угловой скорости лопасти от его угла по отношению водному потоку
На основе (7) выведена зависимость угловой скорости лопасти от его угла к водному потоку (рис. 2). Исходя из графика, когда водный поток ударяется о поверхность лопасти строго перпендикулярно, скорость водяного колеса принимает максимальную величину. При уменьшении угла атаки угловая скорость лопасти падает, как и передаваемая сила. Правильность вывода подтверждается тем, что лопасти имеют наибольший К.П.Д при криволинейной форме исполнения, так как при этом достигается максимально близкое значение к 90° при любом положении лопасти по окружности водяного колеса в водном потоке [5].
Исходя из вышесказанного, можно сделать следующие выводы:
1. Лопасть эффективно работает, когда угол атаки к направлению водного потока максимально приближен к 90 градусам. Лопасть должна изготавливаться криволинейной формы, что обеспечит максимально близкое значение угла атаки к водяному потоку и наибольшую величину передаваемой энергии;
2. Угловая скорость увеличивается с уменьшением радиуса водяного колеса, что позволяет использовать его вместо турбины для тихоходных генераторов;
3. Использование водяных колес эффективно для генерации электроэнергии при малых скоростях водного потока и низких напорах, чем характеризуются малые реки.