Ранее было неоднократно показано [2, 3], что периодичность вообще и периодичность свойств в частности, носит ярко выраженный полиномиальный характер. Предложен общий алгоритм прогноза на основе кубического полинома и вариант формулировки ПЗ, ему соответствующий.
Обратные свойства элементов, простых тел и их соединений находятся в полиномиальной периодической зависимости от обратных значений номеров периодов, в которых эти объекты расположены.
Т.е., если n-номер периода (главное квантовое число), а P-произвольное свойство, то
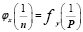 (1)
(1)
Если использовать главное квантовое число n, появляется возможность выявить общую генетическую основу периодичности, что и было сделано [5]. Отметим, что совершенно независимо от наших исследований, проблемой математизации Периодического закона занимались и другие авторы [2, 4, 7 и др.]. По нашему мнению, среди прочих следует особо выделить работу [4], в которой гносеология периодичности также выведена ab initio, предложены оригинальная концепция нуклонных блоков в строении атомов и формулы для определения Z конечных элементов периодов, их массовых чисел А, дефиниция числа нейтронов N в атомах на основе полинома.
В качестве рабочей таблицы химических элементов принят наш вариант модификации лестничной формы Бора-Томсена: секториально-слоевая система со смещениями элементов-аналогов, в которой благородные газы и параллельные им элементы расположены в слоях, а s – элементами и им параллельные – в лучах [1, 5].
Решение уравнения (1) получено в рамках естественных рядов элементов, причём необходимо учитывать неравнозначность чётного и нечётного начал, присущее свершениям Природы. Данный феномен затрагивает самые основы организации материи и уже только вследствие этого не может не вызывать различий в свойствах чётно-(е-) и нечётнопериодных (0-) объектов, подтверждением чему служит явление вторичной периодичности (ВП), открытое ещё Е.В. Бироном [1].
Поэтому поделив естественные ряды на е-о- подмножества и выбрав естественный ряд s- элементов, как наиболее изученный и содержащий наибольшее число известных членов, получаем решения в виде полиномов третьей степени. В качестве испытуемого свойства выберем заряд ядра Z, поскольку эта характеристика абсолютна, целочисленна, не содержит экспериментальных ошибок, она характеризует количество носителей свойств и известна на всём протяжении натурального ряда элементов. В качестве аргумента выбираем n- номер периода, главное квантовое число. Имеем общее решение в виде:
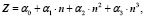 (2)
(2)
которое для семейства благородных газов принимает форму
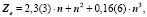 (3)
(3)
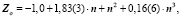 (4)
(4)
Уравнения любого слоя, параллельного благородным газам, аналогичны, за исключением свободного члена αо, который при движении вверх по рисунку [5] с каждым шагом уменьшается на единицу. Например, для галогенов получим:
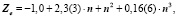 (5)
(5)
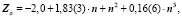 (6)
(6)
Подмножества щелочных элементов описываются уравнениями:
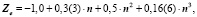 (7)
(7)
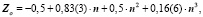 (8)
(8)
Таким образом, для щёлочноземельных имеем:
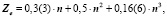 (9)
(9)
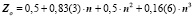 (10)
(10)
и т.д.
Таблица 1
Коэффициенты уравнения (2) для разных совокупностей элементов
|
Характер совокупности |
Примеры |
Значение коэффициентов в уравнении (2) |
||||||||
|
αo |
α1 |
α2 |
α3 |
|||||||
|
Средние элементы семейств |
n |
1 |
3 |
5 |
7 |
9 |
0,5 1,5 |
1,83(3) |
0,5 |
1,16(6) |
|
zo |
– |
15 |
43 |
95 |
179 |
|||||
|
ze |
– |
16 |
44 |
96 |
180 |
|||||
|
n |
2 |
4 |
6 |
8 |
10 |
1,0 2,0 |
1,33(3) |
|||
|
zo |
1 |
14 |
45 |
102 |
193 |
|||||
|
ze |
1 |
15 |
46 |
103 |
194 |
|||||
|
Средние элементы периодов |
n |
1 |
3 |
5 |
7 |
9 |
– 1,25 – 0,25 |
1,33(3) |
0,75 |
0,16(6) |
|
zo |
1 |
14 |
45 |
102 |
193 |
|||||
|
ze |
2 |
15 |
46 |
103 |
194 |
|||||
|
n |
2 |
4 |
6 |
8 |
10 |
– 1,0 0,0 |
||||
|
zo |
6 |
27 |
70 |
143 |
254 |
|||||
|
ze |
7 |
28 |
71 |
144 |
255 |
|||||
Примечание. Показано в [5, 6].
Зависимости для параллельных им лучей отличаются лишь величиной члена αо, который возрастает на единицу при переходе от луча к лучу вниз по рисунку. Уравнения (2)÷(10) являются математическим оправданием ПЗ, которые получают статус обязательного атрибута периодичности.
Ранее было показано [5,6], что коэффициенты αi связаны с теорией чисел, а значение α3 = 0,1666666… присуще исключительно феномену периодичности (табл. 3). Вообще же каждый член системы является пунктом, в котором пересекается множество полиномиальных маршрутов и именно полином в сочетании с явлением чётного – нечётного есть основа структуры генерального множества – Периодической системы (табл. 1).
Следует обратить внимание на несомненную связь коэффициентов уравнения Z = f(n) с константами периодической системы и теорией чисел. Обратившись к табл. 1, отметим следующее:
● разница между αo чёт и нечет в каждом семействе при последовательном движении по ним есть число членов семейства в этом периоде (за исключением s – элементов, для которых она равна – 1);
● разница между α1 чёт и нечет в тех же условиях представляет собой арифметическую прогрессию нечётных натуральных чисел (1, 3, 5, 7, 9…);
● коэффициент α2 для любого семейства равен числу членов этого семейства в периоде; исключение составляют опять – таки s – элементы, у которых α2 = 1;
● в рамках каждого семейства, за исключением s-, коэффициенты α2 одинаковы как в чётных, так и в нечётных последовательностях, поскольку представляют собой число членов данного семейства в периоде;
● суммы коэффициентов α3 в пределах каждого семейства также равны в е- и о- совокупностях, так как являются произведением числа членов семейства в периоде на 0,16(6) – характеристическую константу кубического полинома;
● сумма коэффициентов α3 от семейства к семейству возрастает на одну и ту же величину 0,66(6)…, которая представляет собою произведение характеристической константы кубической параболы на 4 – приращение числа элементов от семейства к семейству [2] и т.д.
Перейдём к прогнозу конкретных свойств веществ (Рх). При этом сразу возникает вопрос, насколько такие оценки будут близки к истине. Для контроля результатов следует прибегнуть к независимым методам, арсенал которых довольно скуден. Во – первых, это различные системы термохимических инкрементов либо чисто эмпирического характера, либо имеющих в своей основе некие модельные представления; среди последних стоит выделить работы Г. Пинаева [3]. Системам инкрементов присущ общий недостаток – необоснованная универсализация, в результате чего на одну прямую пытаются уложить в принципе все катионы при постоянном анионе и наоборот, т.е. пренебрежение о-е- феноменом. Во – вторых, это группа сравнительных методов, основанных на использовании разного рода корреляций в двух рядах свойств или соединений – эталонном (х) и искомом (у). Наибольшее распространение здесь получили параболическое и линейное соответствия. Первое вытекает из классической концепции электроотрицательности Л. Полинга и для энтальпий образования бинарных соединений может быть записано в виде
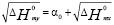 . (11)
. (11)
Недостатки – очень высокие погрешности при коррелировании свойств оксидов, сульфатов, тройных соединений.
Линейные корреляции лежат в основе метода сравнительной термодинамики Карапетьянца-Киреева в котором предполагается наличие приближённых линейных регрессий в рядах однотипных или сходных соединений:
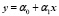 . (12)
. (12)
Однако, в подобной трактовке обсуждаемый приём имеет массу исключений. Авторы сами предостерегают от распространения его на разнотипные соединения вследствие увеличения средней дисперсии регрессии (12), а также из-за отсутствия теоретического обоснования как самой возможности, так и границ расширения способа. Вследствие эффекта кайносимметрии соблюдение формальной однотипности ещё не является гарантией низкой дисперсии регрессии (12), что и имеет место при сопоставлении оксидов с сульфидами, карбонатов с силикатами и тому подобное. Особенно резко это проявляется в сфере обратных задач прогнозирования, когда по заданной характеристике надо подобрать наиболее подходящее вещество. Кроме того, прямая непригодна для графической интерпретации всего разнообразия свойств веществ в широком интервале значений. Она описывает некоторый ограниченный участок, пределы которого указать точно не представляется возможным, поскольку для этого нет чётких критериев.
Поэтому, как стало ясным по мере накопления экспериментального материала, указанный приём в большинстве случаев давал чересчур приближённые оценки, что и стало основной причиной утраты им востребованности. В то же время идея сопоставления характеристик вещества для целей количественного прогноза неизвестных ещё свойств элементов представляется весьма привлекательной. Это побудило нас провести модификацию метода сравнительной термодинамики, согласовав его с концепцией полиномиальности.
Примем во внимание, что поскольку для эталонного ряда в этом случае справедливо
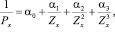 (13)
(13)
то для определяемого мы вправе ожидать
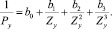 (14)
(14)
Их отношение при αi отличном от bi, или (и) Zx, не равном Z0, будет полиномом того же порядка. Таким образом, вместо (12) мы предлагаем
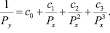 (15)
(15)
Преимущества подхода очевидны: вместо линейки – лекало с гораздо большими возможностями, нежели (12), при его использовании снимаются требования к однотипности или сходности сопоставляемых рядов соединений, и сохраняется лишь условие совместимости. В качестве эталона свойства примем первые потенциалы ионизации щелочноземельных элементов, которые измерены с высокой точностью.
Результаты расчётов по (15) приведены в табл. 2, нижняя строка. Учитывая то, что точность табличных данных для Fr в той или иной мере снижена из-за работы с микроколичествами вещества (~ 10-13М), совпадение с результатами наших расчётов следует признать хорошим. Ход вычислений был следующим. Выбиралось свойство для определения, например, первый потенциал ионизации I1 в ряду 1-11-37-87 и предпринималось сопоставление этого ряда (у) и эталонной последовательности (х). Однако здесь возникает проблема, связанная с тем, что в маршруте H, Na, Rb, Fr четвёртый член сам является определяемым и для установления кубической зависимости недостаёт одной пары х-у. Обойдём это затруднение следующим образом. Воспользуемся тем обстоятельством, что полиноминальные соотношения I1 – Pi, и φ (n) – f(Pi) для одного и того же свойства конкретного элемента должны давать одинаковые результаты. Выбрав в качестве эталона первый потенциал в качестве которого принят ряд для I1 в последовательности 2-12-38-88…, будем приближённо назначать I1 франция до тех пор, пока после нескольких итераций для произвольно выбранного контрольного элемента (мы, в частности, вели сравнение по 169) определяемого ряда он не совпадёт с необходимой точностью по обоим полиномам. Полученная при этом величина и будет являться искомой. Аналогичные операции выполним и для других свойств Fr (табл. 2).
Таблица 2
Определяемые свойства франция
|
Эталон (х) |
Свойства Py |
|||||||||||
|
n |
I1 |
I1 |
ra |
ΔH0(+1) |
ΔG0(+1) |
Тпл |
Ткип |
ΔH0пл |
ЭОо-р |
Cp |
d |
прим. |
|
1 |
24,58764 |
13,59857 |
78 |
1536,21 |
1516,99 |
14,0 |
20,3 |
0,12 |
2,20 |
28,8 |
0,087 |
|
|
3 |
7,64607 |
5,13515 |
192 |
609,60 |
574,59 |
371,2 |
1156,1 |
2,64 |
1,01 |
28,26 |
0,966 |
|
|
5 |
5,69410 |
4,17719 |
248 |
490,16 |
457,87 |
312,7 |
961 |
2,20 |
0,89 |
31,09 |
1,52 |
|
|
7 |
5,2790 |
3,98 |
270 |
462,6 |
433,53 |
291 300* |
913 950* |
2,1 |
0,86 |
31,6 |
2,44 |
табл. |
|
3,97 |
260 |
463 |
433 |
299 |
920 |
2,1 |
0,86 |
32 |
3,18 |
выч. |
||
Примечание. *Оценены разными методами.
Таблица 3
Динамика изменения отношения значений свойств ЩМ/ЩЗМ
|
Св-во Отн-е |
I1 |
r0 |
ΔH0пл |
Sтв |
ЭОп |
Eo |
Тпл |
Ткип |
ΔН0А |
ΔН0+ |
Sгаз |
d |
|
H/He |
0,55 |
1,72 |
0,1 |
– |
– |
– |
0,96 |
0,95 |
– |
0,65 |
0,91 |
– |
|
Na/Mg |
0,67 |
1,34 |
0,29 |
1,56 |
0,82 |
1,15 |
0,40 |
0,83 |
0,62 |
0,68 |
1,03 |
0,49 |
|
Rb/Sr |
0,73 |
1,25 |
0,29 |
1,46 |
0,89 |
1,01 |
0,30 |
0,58 |
0,50 |
0,68 |
1,03 |
0,53 |
|
Fr/Ra |
0,75 |
1,20 |
0,29 |
1,36 |
0,89 |
1,00 |
0,27 |
0,54 |
0,50 |
0,68 |
1,03 |
0,41 |
|
0,53 |
Примечание. В табл. 1–3 символы и размерность величин соответствуют принятым в научной литературе.
Как видно из таблицы, результаты наших определений достаточно хорошо соответствуют справочным во всех случаях, за исключением одного – плотности d, которую мы выражали в (моль/см3)·103. Столь значительный процент совпадений утверждает, по меньшей мере, два принципиальных обстоятельства. Во-первых, достаточно высокую надёжность использованных радиохимических методик; во-вторых, ещё один весомый довод в пользу справедливости развиваемых здесь представлений, так как идентичные результаты получены совершенно различными способами.
Вернемся теперь к показателю плотности d и попытаемся понять причину столь значительного (> 30 % отн.) расхождения данных двух независимых методов. Рассмотрим закономерности изменения соотношений различных свойств в однопериодных парах s – элементов.
Как явствует из табл. 3, численные отношения всех характеристик стремятся и, как правило, монотонно, к некоторым пределам. Эта монотонность резко нарушается, если для франция использовать табличное значение 2,44 г/см3 (0,01094 г – ат/см3), но она восстанавливается, если взять в основу расчёта результат наших определений – 3,18 г/см3 или 0,01427 г – ат/см3 из табл. 2. Таким образом, мы склонны полагать, хотя ссылка на неточность первоисточника есть ultima ratio, что в данном случае причина заключена именно в этом и уточнённое значение плотности металлического франция будет в 1,3 раза выше, чем принято считать в настоящее время.
Аналогичные действия возможны и с чётнопериодными элементами, но главное препятствие здесь – нерешённый спор: правомочно ли продлять таблицу Д.И. Менделеева в область отрицательных n и Z. Ведь тогда она неизбежно пройдёт через нулевой период, который в настоящее время лишён права на существование, хотя начиная от работ Ахумова и Капустинского и кончая современными взглядами. Всегда были и есть сторонники этой парадигмы. Вспомним: ещё великий Резерфорд говорил о нулевом элементе как о реальной вероятности.
Тем не менее, мы можем оценить свойства элементов 119, 120, по уравнению квадратичной параболы. Так для I1 получены E – Fr 3,67, E – Ra 4,82 эВ. Дефинированы важнейшие свойства элементов со 112 по 120 включительно [5, 6].
Таким образом, изложенные нами результаты однозначно подтверждают тезис о том, что Периодический закон – фундаментальное установление Природы, имеющее твёрдую математическую основу и многовариантность: менделеевская периодичность, вторичная, двойная, периодичность семейств, периодов и т.д. Предложенная методика расчёта свойств элементов расширяет возможности прогнозной химии сверхтяжёлых (супернейтронных) элементов, создаёт надёжную основу для компактизации естественнонаучной информации.

