Введение
Задача построения k-значных безызбыточных безусловных диагностических тестов (ББДТ) в интеллектуальных системах не нова и представлена в ряде публикаций, например в [1, 2, 6]. Однако, до сих пор, она не потеряла своей актуальности.
Предлагается построение k-значных ББДТ осуществлять посредством ускоренного шагово-циклического алгоритма с использованием оптимизирующих преобразований матричного описания данных и знаний и матриц, построенных на их основе.
В данной статье приводятся основные понятия и определения, дается постановка задачи, описывается ускоренный шагово-циклический алгоритм построения k-значных ББДТ.
Представление данных и знаний
Данные и знания представляются с использованием матричной модели [1-4, 6], включающей целочисленную матрицу описаний (0, задающую описание объектов в пространстве характеристических признаков z1,z2..,zm и целочисленную матрицу различений (R), задающую разбиение объектов на классы эквивалентности по каждому механизму классификации. Если значение характеристического признака несущественно для объекта, то данный факт отмечается прочерком («-») в соответствующем элементе матрицы Q. множество всех неповторяющихся строк матрицы различений сопоставлено множеству выделенных образов. обозначим через R´ одностолбцовую матрицу, элементами которой являются номера образов.
Под образом будем понимать подмножество объектов базы знаний с совпадающими значениями классификационных признаков. пример матриц Q, R и R´ представим на рис.1.

Построение матрицы импликаций. матрицей импликаций [1]
назовем целочисленную матрицу U, столбцы которой
сопоставлены характеристическим признакам z1,z2,...,z а строки - всевозможным парам объектов a,
b из разных образов.
Строка Ui матрицы U представляет
собой значение елочисленной вектор-функции различения, - я (j∈{1, 2, ..., m}) компонента uij которой вычисляется по следующей формуле:
где qai j , ( qbi j) - значение признака zj для объекта a (b), объекты a,b из разных образов.
Будем говорить, что строка Uk поглощает строку ![]()
![]()
где i∈{1,2, ...,s} - множество строк матрицы U.
Отроки Uk и U несравнимы
![]()
Тестом [5] называется совокупность признаков, различающих любые пары объектов, принадлежащих разным образам.
Тест называется безызбыточным, если содержит безызбыточное количество признаков.
Под закономерностями [4] в знаниях будем понимать следующие подмножества признаков: константные, устойчивые (константные внутри образа), неинформативные (не различающие ни одной пары объектов), альтернативные (в смысле включения в диагностический тест (ДТ)), зависимые (в смысле включения подмножеств различимых пар объектов), несущественные (не входящие ни в один безызбыточный тест (БТ)), обязательные (входящие во все БТ), псевдообязательные (входящие в множество используемых при распознавании БТ и не являющиеся обязательными) признаки, а также все минимальные и все (либо часть - при большом признаковом пространстве) безызбыточные различающие подмножества признаков, являющиеся, по сути, соответственно минимальными и БТ (тупиковыми тестами [5]).
Множество обязательных признаков назовем ядром всех дт, поскольку исключение любого признака из ядра нарушает свойство каждого из тестов быть тестом.Будем определять весовой коэффициент признака (БЮТ) z. по его разделяющей способности [2] и обозначать через wi
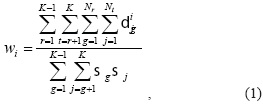
где K - число выделенных образов; N - число строк в описании c-го
образа
(c∈{r,t}); ![]() где qgi (qji) - значение признака zi из образа g (j), g ≠ j; σj - число бъектов в j-ом образе (j=1, ..., K), вычисляемое по формуле:
где qgi (qji) - значение признака zi из образа g (j), g ≠ j; σj - число бъектов в j-ом образе (j=1, ..., K), вычисляемое по формуле: ![]() (d - l - число значений «-» в l-ой строке матрицы Q, pl -
(d - l - число значений «-» в l-ой строке матрицы Q, pl -
коэффициент повторения l-ой строки).
Безызбыточным столбцовым покрытием матрицы импликаций называется подмножество столбцов, покомпонентная сумма элементов которых равна столбцу, состоящему из ненулевых значений, причем, при исключении любого столбца из данного подмножества указанное свойство нарушается. Каждое столбцовое покрытие матрицы импликаций задает полностью различающее подмножество признаков, состоящее из признаков, соответствующих столбцам, входящим в данное покрытие.
Построение сокращенных матриц описания, различений и безызбыточной матрицы импликаций. Сокращенные целочисленные матрицы описания Q´, различений R´ и целочисленная безызбы точная матрица импликаций U´ используются при построении ускоренного шагово-циклического алгоритма. Идея построения матриц изложена в публикации [6].
Построим матрицы Q´ и R´ по матрицам Q и R. каждый образ представляется двумя строками матрицы Q´. каждая четная (нечетная) строка Q´i (Q´f) матрицы Q´ представляет собой целочисленный вектор (i=2c, f=2c-1, c∈ {1, 2, ..., v}, v - количество образов), j-я (j∈{1, 2, ..., m}) компонента которого соответствует максимальному (минимальному) значению j-го ха ракте ристического признака внутри каждого образа и вычисляется по формуле:
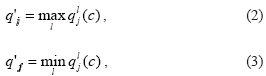
Матрица R´ строится одновременно с построением матрицы Q´.
Заметим, что при построении матрицы Q´ строки из разных образов могут совпадать, вследствие чего образы будут пересекаться, что недопустимо в рамках рассматриваемой матричной модели представления знаний.
С целью обеспечения непересечения образов предлагается использовать правило 1: если строки в матрице Q´ из образов c, e (c Ф e) совпадают, то в матрице Q выбирается строка в одном из выделенных образов, изменение которой приводит к наименьшему изменению значений наименьшего количества признаков в одной из совпадающих строк матрицы Q´, при водящее к непересечению каждой пары образов.
Далее скорректированные матрицы будем обозначать также через Q´ и R´ соответственно.
После процедуры упорядочивания строк в матрицах Q и R (рис.1) и построения матриц Q´ и R´ выявляем, что строки 1 и 3 матриц Q´ и R´ совпадают. Далее осуществляем корректировку матриц Q´ и R´ путем применения правила 1, что приводит к замене значения признака z равное 10 в 1-ой строке, на значение 11, выделеное полужирным шрифтом (рис.2).

По матрицам Q´ и R´ построим сокращеную безызбыточную матрицу импликаций, обозначаемую далее через U´´, строка U´´i которой представляет собой значение целочисленной вектор-функции различения,а j- я (j∈{1, 2, ..., m}) компонента u´´ij вычисляется по формуле:
![]()
К сожалению, рамки доклада не позволяют привести иллюстрирующий пример. Отметим лишь, что при построении k-значных ББДТ по матрицам Q и R (см. рис.1) с использованием ускоренного шагово-циклического алгоритма, количество строк матрицы импликаций при построении сокращенной матрицы импликаций сокращается с 303 до 24.
Постановка задачи построения k-значных ББДТ и алгоритм ее решения. Необходимо: по заданным матрицам Q и R в пространстве k-значных признаков построить матрицу U´´, найти все ее безызбыточные столбцовые покрытия и соответствующие множества характеристических признаков, вошедших в k-значные ББДТ.
Ускоренный шагово-циклический алгоритм построения k-значных ББДТ основывается на идеи ускоренного шагово-циклического алгоритма построения бинарных ББДТ [3] и состоит из следующих шагов:
Упорядочивание строк матриц Q и R по принадлежности к образам.
Построение матриц Q´ и R´ с использованием формул 2, 3 и, в случае пересечения образов, корректировка матриц Q´ и R´ по правилу 1.
Построение матрицы U´´ (формула 4) и вычисление w. по формуле 1. Выделение ядра в матрице U´´ и выявление закономерностей по алгоритму, приведенному в статье [1].
Построение ББДТ с использованием ускоренного шагово-циклического алгоритма [3].
Конец.
При большом количестве ББДТ предлагается осуществлять остановку алгоритма по времени, либо по заданному количеству тестов. Для приведенного примера построено 8 ББДТ: [z2,z3,z4}, [z2,z3,z5}, {z2,z4,z6}, {z2,z5,z6}, {z1,z3,z4,z7}, {z1,z3,z5,z7}, {z1,z4,z6,z7}, {z1,z5,z6,z7}.
Заключение
Предложено построение сокращенных матриц описания и различения и оригинальный ускоренный шагово-циклический алгоритм построения k-значных ББДТ. Предложенный алгоритм сокращает количество переборных процессов, тем самым уменьшая временные затраты на построение k-значных ББДТ.
Дальнейшие исследования связаны с оценкой эффективности алгоритма, разработкой модуля на языке Си++ и включением его в интеллектуальное инструментальное средство ИМСЛОГ [7].
Работа выполнена при поддержке РФФИ (проект № 09-01-99014-рофи).
Список литературы
1. Янковская А.Е. Построение k-значных диагностических тестов в интеллектуальной системе с матричным представлением знаний// Сб. научных трудов VI Национальной конф. по искусственному интеллекту с межд. участ. (КИИ-98). Том I. - Пущино, 1998. - С. 264-269.
2. Янковская А.Е. Логические тесты и средства когнитивной графики в интеллектуальной системе// Новые информационные технологии в исследовании дискретных структур. Доклады 3-ей Всерос. конф. с междунар. участием. - Томск: изд-во СО РАН, 2000. - С. 163-168.
3. Янковская А.Е. Ускоренный шагово-циклический алгоритм построения безызбыточных безусловных диагностических тестов в интеллектуальном инструментальном средстве ИМСЛОГ-2002// Научная сессия МИФИ-2003. Сборник научных трудов. Т. 3. Интеллектуальные системы и технологии. - М.: МИФИ, 2003. - С. 168169.
4 .Гедике А.И., Янковская А.Е. Построение всех безызбыточных безусловных диагностических тестов в интеллектуальном инструментальном средстве ИМСЛОГ// Интеллектуальные системы (AIS´05). Тр. Межд. научн.-техн. конф. Т.1. - М.: Физ-матлит, 2005. - С. 209-214.
5. Журавлев Ю.И., Гуревич И.Б. Распознавание образов и анализ изображений// Искусственный интеллект. Кн. 2. Модели и методы/ Под ред. Д.А. Поспелова. - М.:Радио и связь, 1990. - С. 149-190.
6. Янковская А.Е., Китлер С.В. Оптимизация обработки и хранения k-значной информации в системах искусственного интеллекта// Сб. научных трудов Всерос. конф. с элементами научной школы для молодежи «Проведение научных исследований в области обработки, хранения, передачи и защиты информации». Том 2. - Ульяновск: УлГТУ, 2009. - С. 439-447.
7. Yankovskaya A.E., Gedike A.I., Ame-tov R.V., Bleikher A.M. IMSLOG-2002 Software Tool for Supporting Information Technologies of Test Pattern Recognition// Pattern Recognition and Image Analysis. - 2003. - Vol. 13. - No. 2. - pp. 243-246.

