Все возрастающие требования к защите окружающей среды остро ставят перед предприятиями нефтяной промышленности Республики Казахстан задачу снижения до минимума числа аварий при добыче и транспортировке нефти. В нефтяных месторождениях Узень, Жетыбай, Каражанбас и др. Мангистауской области скопились нефтяные отходы, образовавшиеся в результате аварий, нарушении технологического режима подготовки нефти и технической эксплуатации нефтяных скважин. Аэрофотосъемка показывает наличие большого количества амбаров разлитой нефти, которые загрязняют территорию нефтяных месторождений и оказывают негативное воздействие на окружающую среду. Амбарная нефть является полезным углеводородным сырьем, хотя и претерпела серьезные структурные изменения. Верхний слой затвердел и не поддается излечению. Для сбора конденсированной среды предложен термомеханический способ разжижения амбарной нефти в комплексе с передвижной установкой [1].
Опытно-промышленные испытания установки, проведенные в амбарах месторождения Жалгыз-Тобе (декабрь, 2003 г.), Каражанбас (2004-2005 гг.), Узень (октябрь, 2006 г.) Казахстана показывают, что гидродинамика взаимодействия паровой сверхзвуковой струи с амбарной нефтью подобна развитию неизотермической струи жидкости в конденсированной среде (см. рис. 1). В этой связи ниже рассматривается задача распространение турбулентной неизотермической, круглой струи жидкости в объеме амбарной нефти.

Рис. 1. Фотография струи в амбарной нефти
Математическая модель процесса. Круглая струя жидкости с начальной температурой То, скоростью Uo и расходом Go развивается в высоковязкой среде (резервуар амбарной нефти). Скорость истечения – дозвуковая, температура струи высокая (То=373К) и позволяет подогревать высоковязкую среду. Для простаты анализа предполагается, что жидкость струи имеет такую же физико-химическую свойству, как и амбарная нефть, реологические свойства которой, удовлетворяет модель ньютоновской жидкости. Амбарная нефть имеет температуру (Тw=303К), чуть выше ее температуры застывания, что позволяет не учитывать теплоту плавления высоковязкой среды. По мере развития струи в резервуаре ее скорость затухает, тепло, вносимое горячей струей, подогревает высоковязкую среду и вызывает снижение ее вязкости, тем самым вовлекает амбарную нефть в движение. Теплофизические свойства амбарной нефти считаются функциями от температуры и находятся путем лабораторных исследований. Схема течения и область интегрирования приведены на рис. 2. Для простоты анализа считается, что амбарная нефть находится в емкости цилиндрической формы. Дно и боковые стенки емкости являются твердыми поверхностями, а верхняя часть – свободной, граничащей атмосферным воздухом. Круглая струя горячей жидкости подается по центру емкости и ее движения рассматривается в цилиндрической системе координат, ось OZ направляется по оси движение струи, а ось OR – по радиусу круглой струи. Вследствие осевой симметрии задачи относительно оси OZ рассматривается область с размерами 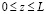 ;
; 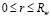 (см. рис. 2).
(см. рис. 2).
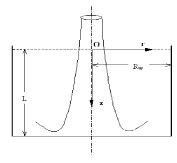
Рис. 2. Схема струи в емкости
Движение струи считается турбулентным и процесс нагрева амбарной нефти – стационарным. Неизотермическое движение жидкости в амбарной нефти описывается системой уравнении Навье-Стокса, осредненной по Рейнольдсу [2, 3], и, имеющей вид.
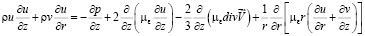 (1)
(1)
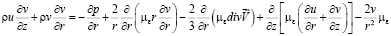 (2)
(2)
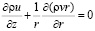 . (3)
. (3)
Уравнение переноса тепла с учетом диссипации кинетической энергии движения можно записать в виде:
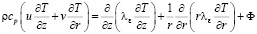 , (4)
, (4)
где 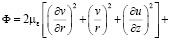 +
+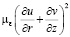 – диссипация кинетической энергии движения в тепло.
– диссипация кинетической энергии движения в тепло.
В уравнениях (1) – (4): z, r – цилиндрические координаты; u, 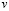 – компоненты вектора скорости
– компоненты вектора скорости  ;
; 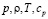 – давления, плотность, температура и теплоемкость жидкости;
– давления, плотность, температура и теплоемкость жидкости; 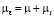 ,
, 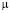 – коэффициент динамической вязкости жидкости,
– коэффициент динамической вязкости жидкости, 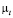 – коэффициент турбулентной вихревой вязкости;
– коэффициент турбулентной вихревой вязкости; 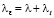 , l – коэффициент теплопроводности жидкости,
, l – коэффициент теплопроводности жидкости, 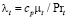 ,
, 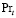 – турбулентный аналог числа Прандтля.
– турбулентный аналог числа Прандтля.
Теплофизические свойства жидкости были найдены по результатам лабораторных исследований амбарной нефти в интервале температуры 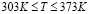 и обобщены в виде эмпирических зависимостей:
и обобщены в виде эмпирических зависимостей:
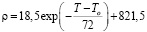 (кг/м3);
(кг/м3);
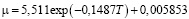 (кг/(м·с)); (5)
(кг/(м·с)); (5)
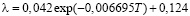 (Вт/(м·град);
(Вт/(м·град);
Теплоемкость жидкости 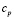 в интервале температуры
в интервале температуры 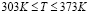 мало меняется и считается постоянной
мало меняется и считается постоянной 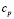 =0,23 кдж/(кг·град).
=0,23 кдж/(кг·град).
Известно, что в инженерных задачах широко используется 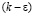 – модель турбулентности и позволяет получить достаточные надежные данные [3-8]. Например, в работе [6] даны результаты сравнения расчета пристенной турбулентной, плоской струи, вытекающей встречный поток в канале, полученные тремя моделями турбулентности: 1) LES-модели турбулентности; 2)
– модель турбулентности и позволяет получить достаточные надежные данные [3-8]. Например, в работе [6] даны результаты сравнения расчета пристенной турбулентной, плоской струи, вытекающей встречный поток в канале, полученные тремя моделями турбулентности: 1) LES-модели турбулентности; 2) 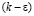 – модели турбулентности для низких чисел Рейнольдса Re; 3) модели турбулентных напряжений с использованием граничных условий в виде закона стенки. Расчеты показывают, что данные полученные
– модели турбулентности для низких чисел Рейнольдса Re; 3) модели турбулентных напряжений с использованием граничных условий в виде закона стенки. Расчеты показывают, что данные полученные 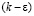 – модели турбулентности для низких чисел Рейнольдса Re, находятся в хорошем количественном согласии с данными LES-модели турбулентности и результатами экспериментальных исследований [7]. В некоторой степени рассматриваемая задача подобна развитию турбулентной струи встречном потоке, что позволяет выбрать для моделирования
– модели турбулентности для низких чисел Рейнольдса Re, находятся в хорошем количественном согласии с данными LES-модели турбулентности и результатами экспериментальных исследований [7]. В некоторой степени рассматриваемая задача подобна развитию турбулентной струи встречном потоке, что позволяет выбрать для моделирования 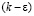 – модель турбулентности. Коэффициент турбулентной динамической вязкости
– модель турбулентности. Коэффициент турбулентной динамической вязкости 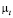 находится на основе
находится на основе 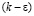 – модели турбулентности, предназначенной для низких чисел Рейнольдса Re, и выражается формулой [8]:
– модели турбулентности, предназначенной для низких чисел Рейнольдса Re, и выражается формулой [8]:
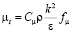 , (6)
, (6)
где 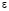 – скорость диссипации кинетической энергии турбулентности,
– скорость диссипации кинетической энергии турбулентности, 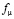 – пристеночная функция, равная [8]:
– пристеночная функция, равная [8]: 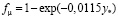 .
.
Дифференциальные уравнения кинетической энергии турбулентности и скорости ее диссипации имеют вид:
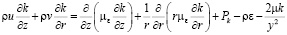 (7)
(7)
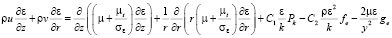 (8)
(8)
где 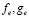 – пристеночные функции, равные [8]:
– пристеночные функции, равные [8]:
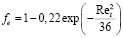 ,
, 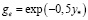 . (9)
. (9)
Константы 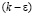 – модели равны
– модели равны 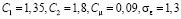 .
.
Число Прандтля 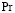 находится при начальной температуре жидкости
находится при начальной температуре жидкости 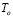 и принимается, равным
и принимается, равным 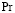 = 0,9. Турбулентный аналог числа Прандтля
= 0,9. Турбулентный аналог числа Прандтля 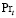 по данным [9,12] можно взять, равным
по данным [9,12] можно взять, равным 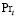 = 0,9. Для удобства решения уравнение переноса тепла записывается относительно избыточной температуры
= 0,9. Для удобства решения уравнение переноса тепла записывается относительно избыточной температуры 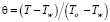 , где
, где 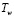 – температура нефти в ложе амбара.
– температура нефти в ложе амбара.
Система уравнений (1) – (9) приводится к безразмерным переменным. Координаты z, r делятся на радиус входного сечения струи; компоненты скорости u, v – на максимальную скорость струи на входе; давление р – на максимальное значение динамического напора струи; температура Т – на То; плотность, коэффициенты динамической вязкости, теплопроводности, теплоемкости – на значения этих величин при температуре То.
Граничные условия задачи имеют вид:
при z = 0:
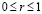 ;
;  ;
; 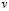 =0;
=0; 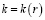 ;
; 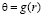 ;
; 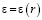 (10)
(10)
при z = 0:
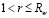 ;
; 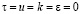 ; –
; – 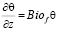 ; (11)
; (11)
при z = L:
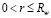 ;
; 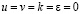 ; –
; – 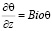 ;
;
при r = 0:
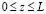 ;
; 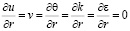 ; (12)
; (12)
при r = Rw: 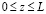 ;
; 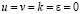 ; –
; – 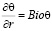 .
.
где t – касательное напряжение; Bio – число Био.
Граничные условия на верхней границе (z = 0) для осевой компоненты скорости, кинетической энергии турбулентности и скорости ее диссипации, избыточной температуры во входном сечении струи (10) соответствуют развитому течению круглой турбулентной струи, а вне области втекания струи (11) ставятся условия на свободной поверхности (равенство нулю касательного напряжения [9]). На нижней твердой поверхности (z = L) ставятся условия прилипания и теплообмен с окружающей средой. На левой границе (r = 0) – условия симметричности течения, а на правой границе (r = Rw) – условия прилипания и теплообмен с окружающей средой.
Система уравнений (1) – (9) с граничыми условиями (10) – (12) решается численным методом в переменных функция тока и напряженность вихря [10 – 13]. Функция тока 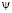 вводится, удовлетворяя уравнения неразрывности движения, посредством равенств:
вводится, удовлетворяя уравнения неразрывности движения, посредством равенств:
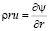 ,
, 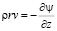 , (13)
, (13)
а напряженность вихря 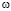 – стандартным выражением:
– стандартным выражением:
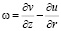 . (14)
. (14)
Подставляя (13) в (14), получим уравнение для функции тока:
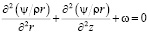 . (15)
. (15)
Из системы уравнения движения, исключая давления, стандартным образом можно получить уравнение для напряженности вихря [10-12]:
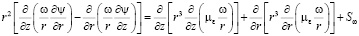 , (16)
, (16)
где 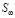 – источниковый член определяется также, как в [10].
– источниковый член определяется также, как в [10].
Граничные условия для уравнения (15), (16) получаются из (10) – (12):
при z = 0: 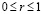 ;
; 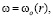
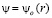 ,
, 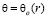 ,
, 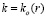 ;
; 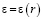
при z = 0:
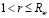 ;
; 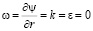 ; –
; –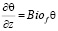 ; (17)
; (17)
при z = L: 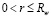 ;
; 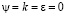 ; –
; –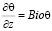 ;
; 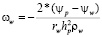
при r = 0: 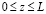 ;
;  ;
;
при r = Rw:
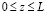 ;
; 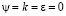 ; –
; –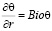 ;
; 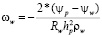 . (18)
. (18)
Как видно из (18), на твердых поверхностях граничные условия для напряженности вихря определяются по формуле Тома [10, 11].
Уравнения для напряженности вихря, переноса тепла, кинетической энергии турбулентности и скорости ее диссипации были аппроксимированы гибридной схемой [10-13]. Разностные аналоги уравнения рассчитывались методом верхней релаксации [11,12].
Для апробации математической модели и численного метода решена задача – расчет турбулентной, плоской струи воздуха набегающей на плоскую нагретую стенку. Расчетные данные по определению местного числа Стэнтона, выражающего теплообмен между стенкой и обтекаемым потоком, были сопоставлены с расчетами Сполдинга [10] и экспериментальными данными Гардона и Акифрата [14] (см. рис. 3).
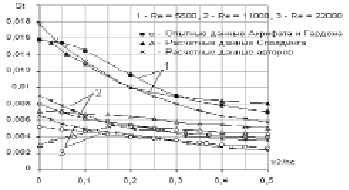
Рис. 3. Верификация численного метода расчета
Результаты сравнения показывают, что при больших числах Рейнольдса (Re=11000, 22000) расчетные данные находятся в удовлетворительном качественном и количественном согласии с опытными данными [14]. При значении числа Рейнольдса (Re=5500) имеется количественное отклонение расчета с экспериментом, хотя качественное согласие зависимости местного числа Стэнтона довольно хорошее (см. рис. 3). Следует отметить также, что закономерности турбулентных струйных течений, как: 1) линейный закон развития границы струи; 2) подобия по числу Рейнольдса динамических и тепловых характеристик осредненного и пульсационного движения хорошо выполняются в расчете.
Обсуждение расчетных данных. Основные режимные параметры течения – число Рейнольдса Re (рассчитанное по средней скорости и диаметру на входном сечении струи); число Bio (выражающее теплообмен жидкости на дне и боковой стенке резервуара); число Biof (выражающее теплообмен жидкости на открытой поверхности); отношения hc/Rc, Rw/Rc, где hc – расстояние между соплом и дном резервуара, а Rc, Rw, – радуисы сопла и резервуара, соответственно; ламинарное Pr и турбулентное Prt числа Прандтля.
На рис. 4 – 6 приведены изолиний напряженности вихря 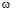 , функций тока
, функций тока 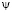 , вектора скорости
, вектора скорости 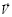 , избыточной температуры
, избыточной температуры 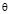 , кинетической энергии турбулентности k и турбулентной вязкости
, кинетической энергии турбулентности k и турбулентной вязкости 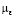 при Re = 11000, Bio = 1, Biof = 5, Prt = 0,9, hc/Rc = 29 и Rw/Rc = 5,6. Теплообмен на свободной поверхности гораздо выше, чем на стенках резервуара, поэтому в расчетах Biof принимается гораздо больше, чем Bio.
при Re = 11000, Bio = 1, Biof = 5, Prt = 0,9, hc/Rc = 29 и Rw/Rc = 5,6. Теплообмен на свободной поверхности гораздо выше, чем на стенках резервуара, поэтому в расчетах Biof принимается гораздо больше, чем Bio.
Структура течения состоит из трех частей: 1) струйная часть течения, направленная на дно амбара; 2) область возвратных течений в вихре; 3) течение в пограничном слое боковой стенки резервуара, направленное на свободную поверхность резервуара.
По распределениям функций тока 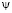 , вектора скорости
, вектора скорости 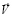 , избыточной температуры
, избыточной температуры 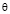 можно судить о закономерности развития неизотермической турбулентной струи в амбарной нефти. В отличие от известного линейного закона изменения границы турбулентных струйных течений в затопленном пространстве [2], граница исследуемого струйного течения сильно искривлена и расширена (см. рис. 4,а). Такое поведение границы струи в амбарной нефти можно объяснить сильной зависимости вязкости нефти от температуры. Амбарная нефть находится при температуре окружающей среды (Тw = 303K) и постепенно вовлекается в струйное движение за счет силы трения. Горячая струя (То=373K) нагревает амбарную нефть путем конвективного перемешивания, молярной и молекулярной теплопроводности и диссипацией механической энергии в тепло. Величина избыточной температуры максимальна на оси и снижается к границам струи, а вязкость нефти, наоборот, принимает минимальное значение на оси струи и возрастает вне струйной части течения. Причем в начале расчетной области отношение максимального и минимального значения вязкости достигает по сечению струи
можно судить о закономерности развития неизотермической турбулентной струи в амбарной нефти. В отличие от известного линейного закона изменения границы турбулентных струйных течений в затопленном пространстве [2], граница исследуемого струйного течения сильно искривлена и расширена (см. рис. 4,а). Такое поведение границы струи в амбарной нефти можно объяснить сильной зависимости вязкости нефти от температуры. Амбарная нефть находится при температуре окружающей среды (Тw = 303K) и постепенно вовлекается в струйное движение за счет силы трения. Горячая струя (То=373K) нагревает амбарную нефть путем конвективного перемешивания, молярной и молекулярной теплопроводности и диссипацией механической энергии в тепло. Величина избыточной температуры максимальна на оси и снижается к границам струи, а вязкость нефти, наоборот, принимает минимальное значение на оси струи и возрастает вне струйной части течения. Причем в начале расчетной области отношение максимального и минимального значения вязкости достигает по сечению струи 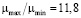 . Высокая вязкость нефти и ее зависимость от температуры и является причиной резкого расширения границы струи. Кроме того, в систему уравнений входит турбулентная вязкость
. Высокая вязкость нефти и ее зависимость от температуры и является причиной резкого расширения границы струи. Кроме того, в систему уравнений входит турбулентная вязкость 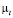 , характеризующая влияние турбулентных напряжений на структуру течения. Картина изолиний
, характеризующая влияние турбулентных напряжений на структуру течения. Картина изолиний 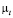 показывает распределения турбулентной вязкости в расчетной области (см. рис. 4,b). Нетрудно заметить, что существует поле максимальных значений
показывает распределения турбулентной вязкости в расчетной области (см. рис. 4,b). Нетрудно заметить, что существует поле максимальных значений 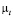 , охватывающее, зону взаимодействия струей с возвратным течением и область торможения струи. Большие значения
, охватывающее, зону взаимодействия струей с возвратным течением и область торможения струи. Большие значения 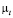 и тем самым турбулентных напряжений обусловлены генерацией энергии турбулентности в этих областях.
и тем самым турбулентных напряжений обусловлены генерацией энергии турбулентности в этих областях.
На процессы переноса существенное влияние оказывает структура течения в вихре, подобная тору, расположенная с центром в правой части расчетной области (см. рис. 5,a). Замкнутые изолиний функции тока 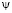 характеризуют вовлечение в вихревое движение массу жидкости из амбарной нефти. В застойной зоне жидкость слабо вращается, перенося тепло горячей струи в холодную часть, и, подогревая амбарную нефть. Изолиний напряженности вихря
характеризуют вовлечение в вихревое движение массу жидкости из амбарной нефти. В застойной зоне жидкость слабо вращается, перенося тепло горячей струи в холодную часть, и, подогревая амбарную нефть. Изолиний напряженности вихря 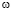 заметны в струйной части течения и на боковой стенке, а в остальной части их величины незначительны (см. рис. 5,b).
заметны в струйной части течения и на боковой стенке, а в остальной части их величины незначительны (см. рис. 5,b).
Картину течения более детально раскрывают изолиний вектора скорости 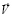 (см. рис. 6). В струйной части вектор скорости направлен вниз, вблизи ее границ наблюдается вовлечение жидкости в движение. Струя натекает на дно резервуара, что приводит к изменению направления вектора скорости на 90о и иллюстрирует обтекание твердой поверхности. В застойной зоне вихря видно возвратное течение жидкости. Вдоль боковой стенки вектор скорости направлен вертикально вверх и вблизи свободной поверхности изменяет свое направление на обратное и показывает взаимодействие струи с амбарной нефтью.
(см. рис. 6). В струйной части вектор скорости направлен вниз, вблизи ее границ наблюдается вовлечение жидкости в движение. Струя натекает на дно резервуара, что приводит к изменению направления вектора скорости на 90о и иллюстрирует обтекание твердой поверхности. В застойной зоне вихря видно возвратное течение жидкости. Вдоль боковой стенки вектор скорости направлен вертикально вверх и вблизи свободной поверхности изменяет свое направление на обратное и показывает взаимодействие струи с амбарной нефтью.
а b
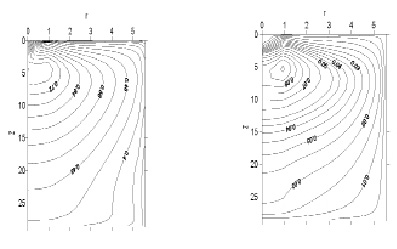
Рис. 4. Изолинии избыточной температуры (а) и турбулентной вязкости (b)
a b
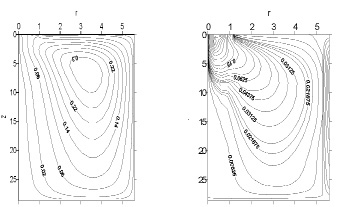
Рис. 5. Изолинии функции тока (а) и завихренности (b)
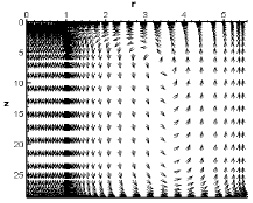
Рис. 6. Картина вектора скорости
Таким образом, общую картину течения можно представить, как вовлечение струей в рециркуляционное движение жидкости в резервуаре. Во всей части течения преобладает конвективный процесс подогрева амбарной нефти. Подсос вихрем горячей жидкости из струи и смешение ее с холодной амбарной нефтью в пограничном слое у боковой стенки и эжектирование жидкости у поверхности амбара в возвратном течении интенсифицирует процесс подогрева и даны по изолиниям вектора скорости. Тепло диссипации кинетической энергии рассеивается конвекцией, молярным переносом и появление локальных зон разогрева за счет тепла диссипации не проявляется. В распределениях изолиний кинетической энергии турбулентности k существует область максимума энергии турбулентности (см. рис. 7,а). В этой зоне происходит интенсивная генерация энергии турбулентности, вызванная эжектированием струей амбарной нефти. В остальной части течения не так заметно изменение кинетической энергии турбулентности.
Аналогичный характер поведения наблюдается в распределениях изолиний скорости диссипации кинетической энергии турбулентности (см. рис. 7,b). Здесь также максимальное значение скорости диссипации достигается в зоне вовлечения струей амбарной нефти, а в остальной части их величины малы. Расчетные данные турбулентных характеристик течения показывают, что молярный перенос существенную роль играет в струйной части и вихревой зоне. В остальной части течения превалируют конвекция и молекулярный механизм переноса импульса и тепла. Коэффициент турбулентной теплопроводности 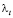 , определяемый по
, определяемый по 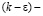 модели турбулентности, выражающий молярный перенос тепла, изменяется подобным образом, как
модели турбулентности, выражающий молярный перенос тепла, изменяется подобным образом, как 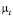 . Эти данные подтверждают подобия процессов переноса тепла и импульса в турбулентных потоках. В расчетах найдено влияние число Рейнольдса Re = 22000, Re = 44000 на процессы переноса в амбарной нефти без изменения других режимных параметров.
. Эти данные подтверждают подобия процессов переноса тепла и импульса в турбулентных потоках. В расчетах найдено влияние число Рейнольдса Re = 22000, Re = 44000 на процессы переноса в амбарной нефти без изменения других режимных параметров.
Картины распределения динамических, тепловых характеристик, переносных свойств подобны качественно соответствующим рисункам 4 – 7, имеются количественные различия, вызванные интенсификацией турбулентного переноса с ростом числа Рейнольдса Re.
Таким образом, расчетные данные подтверждают подобия процессов переноса в турбулентном потоке и показывают правильность созданной математической модели течения, удовлетворяющей закон подобия турбулентности по числу Рейнольдса.
a b
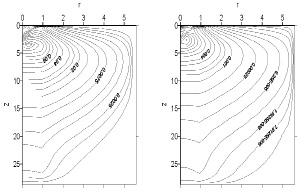
Рис. 7. Изолинии кинетической энергии турбулентности (а) и скорости диссипации кинетической энергии (b)
Заключение. В заключение можно сделать следующие выводы.
1. Изучено развитие турбулентной неизотермической струи в амбарной нефти с использованием RANS модели. Система уравнений RANS модели решается с известным численным методом.
2. Верификация численного метода решения показывает хорошее согласие расчетных данных с экспериментальными данными. Двухпараметрическая 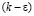 – модель турбулентности при низких числах Рейнольдса качественно хорошо раскрывает основные закономерности процессов переноса импульса и тепла при взаимодействии неизотермической струи с амбарной нефтью.
– модель турбулентности при низких числах Рейнольдса качественно хорошо раскрывает основные закономерности процессов переноса импульса и тепла при взаимодействии неизотермической струи с амбарной нефтью.
3. Показана, что структура течения состоит из трех частей: 1) струйная часть течения; 2) возвратное течение в вихре тороидальной формы; 3) течение в пограничном слое вязкой жидкости вблизи боковой стенки емкости.
4. Расчетные данные показывают, что турбулентный (молярный) перенос существенную роль играет в струйной части и вихревой зоне возвратного движения. В остальной части превалируют конвекция и молекулярные механизмы переноса импульса и тепла.
5. Расчетные данные подтверждают подобия процессов переноса в турбулентном режиме потока и показывают правильность созданной математической модели течения, удовлетворяющей закон подобия турбулентности по числу Рейнольдса.
6. Разработанные математическая модель и численный метод расчета позволяют рассмотреть и исследовать процесс подогрева амбарной нефти струей горячей жидкости. В техническом аспекте позволяет определить массу амбарной нефти подогреваемой до нужной температуры для осуществления термомеханической технологии сбора разлитой нефти.

