Вопросам расчета потерь напряжения и мощности в электрических сетях при наличии отклонение параметров качества электрической энергии от требуемых нормативных значений, в частности при наличии несимметрии токов и напряжений, посвящен ряд публикаций [1, 4, 5, 7, 8].
Но в большом разнообразии известных методик расчета потерь типичным остается допущение, что выражения, применяемые в них при расчетах, справедливы при условии потребления мощностей потребителями в неискаженном (номинальном) режиме. Связно это с тем, что при проектировании работа электрических сетей предполагается в номинальном, симметричном, синусоидальном и равномерно активном режиме.
Вместе с тем, основываясь на результаты практических измерений [2, 3], можно утверждать, что в настоящее время в действующих электрических сетях довольно часто распространено явление длительной фазной несимметрии нагрузки.
Как известно, длительные несимметричные режимы возникают в первую очередь при пофазной разнице параметров системы, либо в случае неполнофазных режимов работы электрооборудования или при подключении несимметричных нагрузок [4, 5, 8].
При таких режимах работы в сети присутствует как амплитудная, так и угловая несимметрия токов и соответственно напряжений, приводящие в свою очередь к появлению токов и напряжений с порядком следования фаз отличного от прямого – обратной и нулевой последовательности.
Тем не менее, в применяемых в практике методах расчета потерь соотношения между токами и напряжениями различных фазовых последовательностей не учитываются. Данное обстоятельство осложняет определение первопричин, вызывающих увеличение дополнительных потерь мощности и целесообразность применения способов их ограничения.
Рассмотрим наиболее широко известные и применяемые способы учета влияния несимметрии нагрузок фаз при расчете величины потери мощности.
Основной директивной методикой по расчету потерь является приказ Министерства энергетики РФ от 30 декабря 2008 г. №326 «Об организации в Министерстве энергетики Российской Федерации работы по утверждению нормативов технологических потерь электроэнергии при ее передаче по электрическим сетям» [6]. Согласно [6] при определении потерь электроэнергии в сетях 0,38 кВ для учета неравномерности распределения нагрузок по фазам, рекомендуется применять коэффициент KHEP [4]:
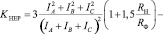
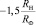, (1)
где RH/RФ – отношение сопротивлений нулевого и фазного проводов;
IA, IB, IC – измеренные токи фаз.
В случае отсутствия достоверных данных о токовых нагрузках фаз в соответствии с вышеуказанным приказом допускается принимать значение KHEP равным:
– KHEP = 1,13, при RH/RФ = 1;
– KHEP = 1,2 при RH/RФ = 2.
В работе [4], в качестве одного из количественных показателей, характеризующих схему сети на основе объективных данных, для выведения зависимости потерь от несимметрии нагрузки, предлагается использовать коэффициент неодинаковости нагрузок фаз (несимметрии токов) KHEС(KHН)
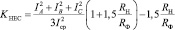, (2)
где RH и RФ – сопротивления нулевого и фазного проводов;
IA, IB, IC – токи фаз;
ICР – среднее значение токов фаз.
В практических расчетах, в случае сложности (невозможности) измерения токов фаз во всех линиях на балансе рекомендуется применять при RH/RФ = 1÷15 средние значения вышеуказанного коэффициента [4]:
– KHEС = 1,35 ± 0,2, для линий с распределенной нагрузкой;
– KHEС = 1,05 ± 0,05, для линий с сосредоточенной нагрузкой.
Различие значений KHEС для разного типа расположения нагрузок связано с предположением, что линии с сосредоточенными нагрузками имеют большую долю симметричных, трехфазных нагрузок, чем линии с распределенными нагрузками.
Согласно [5] определено, что при расчете потерь мощности, также необходимо принимать во внимание дополнительные потери от несимметрии нагрузки. Для этого предлагается использовать коэффициент KДi, учитывающий дополнительные потери от неравномерности нагрузки фаз:
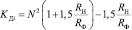, (3)
где RH и RФ – сопротивления нейтрального и фазного проводов;
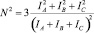– коэффициент неравномерности;
IA, IB, IC – измеренные токи фаз.
Сопоставляя выражения (1) – (3), можно утверждать, что в случае расчета по измеренным величинам токов фаз значений KHEP, KHEС, KДi для одной и той же линии (схемы) будут получены идентичные результаты.
Обусловлено это вследствие равенства 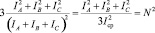(4)
. (4)
В работе [1] указывается, что для сетей 0,38 кВ потери мощности определяются аналогично потерям в сетях 6–10 кВ, но только с учетом важного для сетей 0,38 кВ явления – несимметричной загрузки фаз. Данную «особенность» сетей 0,38 кВ предлагается учитывать через коэффициент неравномерности загрузки фаз – KH [1].
Коэффициент увеличения потерь KH при неравномерной нагрузке фаз, согласно [1] может быть рассчитан по формуле:
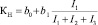, (5)
где I1, I2, I3 – токи фаз в режиме максимальной нагрузки, индекс 1 соответствует наиболее нагруженной фазе;
b0, b1 – статистические коэффициенты, значения которых зависят от характера нагрузки (для коммунально-бытовой нагрузки b0 = 0,37; b1 = 3,92; для смешанной нагрузки b0 = 0,18; b1 = 2,34).
Как видно из выражений (1)–(5), определенные с их помощью значения потерь мощности не учитывают возможность наличия наряду с амплитудной и угловой несимметрии, когда углы сдвига фаз линейных токов по отношению к своим фазным напряжениям не одинаковы.
Увеличение дополнительных потерь мощности по сравнению с симметричным режимом при наличии угловой несимметрии в соответствии с [8] можно учесть с помощью коэффициента KДПH:
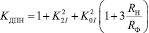, (6)
где K2I, K0I – коэффициенты несимметрии токов по обратной и нулевой последовательности;
RH и RФ – сопротивления нулевого и фазного проводов.
В тоже время в работе [8] на основании наличия в четырехпроводных сетях 0,38кВ неравенства (7), и предположения о практически одинаковом характере нагрузок отдельных фаз, допускается возможность пренебречь величиной угловой несимметрии токов при расчете дополнительных потерь мощности:
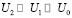, (7)
где U1 – напряжение прямой последовательности;
U2 – напряжение обратной последовательности;
U0 – напряжение нулевой последовательности.
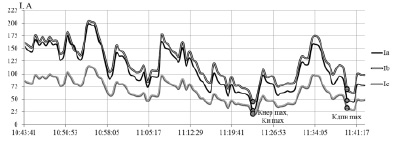
Рис. 1. Графики изменения токов фаз А, В, С
Рис. 2. Графики изменения коэффициента мощности cos φ фаз А, В, С
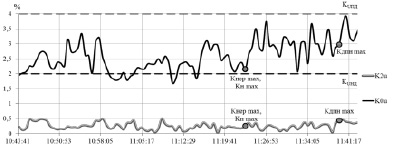
Рис. 3. Графики изменения коэффициентов несимметрии напряжений по обратной (K2U) и нулевой (K0U) последовательности
Рис. 4. Графики изменения коэффициентов несимметрии токов по обратной (K2i) и нулевой (K0i) последовательности
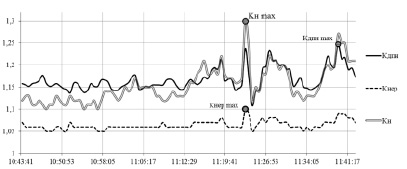
Рис. 5. Графики изменения коэффициентов (Кдпн, Кнер, Кн), учитывающих несимметричный характер нагрузки
Для оценки и анализа возможных результатов значений коэффициентов, учитывающих дополнительные потери мощности от несимметрии нагрузки, произведен их сравнительный расчет на основе реальных данных, полученных в ходе измерений показателей качества электрической энергии.
В качестве опытных данных выбраны значения, полученные при измерении показателей качества и основных параметров электрической энергии в распределительных сетях 0,38 кВ предприятия строительной отрасли (рис. 1–4).
Исходя из анализа полученных данных и графиков (рис. 1–4), можно утверждать о наличии в сети амплитудно-фазовой несимметрии напряжений и токов. Как видно из графика на рис. 5, коэффициент несимметрии по нулевой последовательности напряжения K0U, за выбранный интервал, превышает нормально допустимое значение, что говорит о наличии подключенной к исследуемому центру питания искажающей симметрию нагрузке.
Аналогичным образом на это указывает рис. 4, где токи обратной и нулевой последовательности составляют соответственно 12÷26 % и 12÷22 % относительно тока прямой последовательности.
На основании данных полученных (для RH = RФ) с помощью выражений (2), (5), (6) был осуществлен расчет коэффициентов, учитывающих в той или иной мере дополнительные потери мощности.
По результатам расчетов построены графические зависимости (рис. 5), на которых, в том числе, отображены метки максимальных значений каждого из рассчитываемых коэффициентов – KНЕРmax, KНmax, KДПНmax.
Дополнительно, соответствующие рассчитанным максимальным значениями коэффициентов KНЕР, KН и KДПН метки указаны и на остальных графиках, для визуального определения и соотнесения необходимого электрического параметра режима.
Таблица 1
Сопоставление коэффициентов KНЕР, KН и KДПН и электрических параметров исследуемого участка сети
|
Коэффициент |
Измеренные электрические параметры |
||||||
|
Обозначение |
Максимальное значение |
Ua, В |
Ub, В |
Uc, В |
Ia, А |
Ib, А |
Ic, А |
|
KНЕР |
1,1 |
225,12 |
233,05 |
229,58 |
27,76 |
45,33 |
21,54 |
|
KН |
1,3 |
||||||
|
KДПН |
1,248 |
224,99 |
238,26 |
233,3 |
47,91 |
70,65 |
33,06 |
Таблица 2
Сопоставление коэффициентов KНЕР, KН и KДПН и показателей качества электрической энергии исследуемого участка сети
|
Коэффициент |
Измеренные электрические параметры и показатели качества электрической энергии |
|||||||
|
Обозначение |
Максимальное значение |
cos φa |
cos φb |
cos φc |
K2U, % |
K0U, % |
K2I, % |
K0I, % |
|
KНЕР |
1,1 |
0,84 |
0,8 |
0,82 |
0,27 |
2,16 |
23,45 |
21,99 |
|
KН |
1,3 |
|||||||
|
KДПН |
1,248 |
0,57 |
0,62 |
0,52 |
0,45 |
2,98 |
20,83 |
22,73 |
Максимальные значения рассчитанных коэффициентов KНЕР, KН, KДПН и соответствующие им значения параметров электрической энергии и показателей качества электрической энергии представлены в табл. 1 и 2.
Среднее значение KНЕР определенное по (1) свидетельствует о возможном увеличение потерь за исследуемый период на 6 %, при аналогичных входящих данных выражения (5) и (6) дают средний результат KН и KДПН в 16 % и 17 % соответственно.
Полученные результаты указывают, на сколько потери мощности с учетом несимметрии могут превышать потери мощности, обусловленные протеканием только токов прямой последовательности в исследуемой сети за выбранный временной интервал.
Проанализировав результаты расчетов и полученные зависимости можно утверждать, что в случае наличия в сети амплитудно-фазовой несимметрии, необоснованное использование вышеуказанных методов учета дополнительных потерь мощности, может привести к различию фактического влияния несимметрии токов и напряжений на величину потерь и полученных при расчете дополнительных потерь мощности оценочных значений.