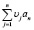Многокритериальный подход означает оценку и выбор оптимального варианта одновременно по нескольким критериям (показателям) в отличие от существующего выбора по единственному экономическому критерию: приведенным затратам, прибыли, рентабельности, чистому дисконтированному доходу. При выборе оптимального варианта по критерию «минимум приведенных затрат» сравниваются, как правило, несопоставимые по другим показателям варианты, следовательно результаты могут получиться необъективными, что делает целесообразным переход к оценке по нескольким критериям. Поэтому необходимо принимать решение с учетом достижения различных, иногда даже противоречивых целей, которое базируется на основе современных экономических методик. Очень часто наряду с минимумом затрат стараются обеспечить максимум надежности электроснабжения, минимум расхода цветного металла и максимум производительности труда [1, 2].
Выбор критериев оценки вариантов следует осуществлять на основе анализа целей функционирования системы. При оценке оптимального варианта по многокритериальной модели необходимо учитывать специфику назначения, условия сооружения, функционирования и эксплуатации рассматриваемых систем.
Кроме многокритериальности задачи оптимизации характеризуются неопределенностью части исходной информации, например такой, как цены на оборудование, тарифы на электроэнергию, закон изменения электрических нагрузок, значения ущербов от перерывов электроснабжения и ухудшения качества электрической энергии и другие. Для неопределенной информации можно указать границы интервала значений от минимума до максимума. Существует множество методом решения оптимизационных задач [5].
Рассмотрим вопрос решения этой проблемы на примере выбора наиболее экономичного варианта схемы районной электрической сети из шести возможных стратегий.
Алгоритм решения многокритериальной задачи методом векторной оптимизации
Чтобы выбрать оптимальный вариант развития электрической сети необходимо решать многокритериальную задачу. В качестве критериев оптимизации можно использовать такие важнейшие показатели, как пропускная способность линии, надежность электроснабжения, капитальные затраты, потери электроэнергии и другие. Такого рода задачи называют задачами векторной оптимизации, так как совокупность критериев эффективности по разным целям образуют вектор критериев [4]. Выбор и обоснование частных критериев оценки является одним из самых важных вопросов. Процедура их выбора носит творческий характер. Критерии должны описывать по возможности все важные аспекты цели, но при этом желательно минимизировать число некоторых критериев. Для этой цели вводят ограничения. Между целевыми критериями и ограничениями имеются сходства и различия. Общее заключается в том, что и критерий, и ограничения являются математической формулировкой некоторых условий. В некоторых задачах оптимизации они могут выступать равноправно. Однако на этапе формирования целевой функции критерий открывает возможности для генерирования новых альтернатив в поисках лучшей из них, а ограничение заведомо уменьшает их число [3].
Критерии выбираются в зависимости от поставленной цели и набор их должен быть как можно более полным, но при этом критерии не должные дублировать друг друга.
Рассмотрим алгоритм решения многокритериальной задачи методом векторной оптимизации на конкретном примере.
Разработка вариантов (стратегий) развития сети с целью повышения пропускной способности.
Для выбора оптимального решения необходимо составить множество стратегий (вариантов) развития сети Ф = (φ1… φi) по нескольким частным критериям F = (f1, fi. f n).
Рассмотрим шесть альтернативных вариантов развития электрической сети с разными типами опор и проводов.
Выбор системы частных критериев, оценивающих степень достижения целей функционирования системы.
Выбор критериев оценки вариантов производится на основе анализа целей функционирования системы, опираясь на понятие результативности и полезности. Полезность вытекает из основного назначения электрической сети и целей ее функционирования. Основное назначение электрической сети – передача и распределение электрической энергии. Её основные цели – обеспечение потребителей электроэнергией с заданным уровняем надежности. Таким образом пропускная способность, потери мощности и капитальные затраты должны включаться в набор частных критериев [6].
Критерии будем называть локальными или частными, и обозначать fi , i =1…n, где i индекс локального критерия, n – число этих критериев. Если критерии имеют различные единицы измерения, то их требуется нормализовать. Разработано большое количество схем нормализации, большинство из которых основываются на введении идеальных значений критериев, с помощью которых, вектор критериев приводиться к безразмерной форме. Каждая компонента вектора может принимать значения в диапазоне (0;1).
Составим матрицу частных критериев. В табл. 1 представлены показатели шести вариантов развития электрической сети.
Критерии достижения целей имеют разные единицы измерения, поэтому необходимо провести нормирование частных критериев по формулам:
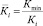 , (1)
, (1)
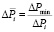 , (2)
, (2)
Таблица 1
Матрица локальных критериев
|
Стратегии |
Пропускная способность, Рi [МВт] |
Капитальные затраты, Кi [млн. руб.] |
Потери мощности, ΔРi [МВт] |
|
φ1 |
63,08 |
352,9 |
1,35 |
|
φ2 |
104,33 |
486 |
1,24 |
|
φ3 |
98,67 |
480 |
0,662 |
|
φ4 |
139,28 |
417 |
0,646 |
|
φ5 |
190,88 |
732 |
0,646 |
|
φ6 |
197,34 |
664,8 |
0,166 |
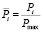 , (3)
, (3)
где Кmin – минимальные капитальные вложения из ряда стратегий, млн руб.;
Кi – капитальные вложения i-й стратегии, млн руб.;
ΔPmin – минимальные потери мощности из ряда стратегий, МВт;
ΔPi – потери мощности i-й стратегии, МВт;
Pmax – наибольшая передаваемая мощность, МВт;
Pi – передаваемая мощность i-й стратегии, МВт.
Результаты нормирования сведены в табл. 2.
Таблица 2
Матрица нормированных критериев
|
Стратегии |
|
|
|
|
φ1 |
0,32 |
1,0 |
0,12 |
|
φ2 |
0,53 |
0,73 |
0,13 |
|
φ3 |
0,5 |
0,74 |
0,25 |
|
φ4 |
0,71 |
0,85 |
0,26 |
|
φ5 |
0,97 |
0,43 |
0,26 |
|
φ6 |
1,0 |
0,53 |
1,0 |
Для комплексной оценки эффективности вариантов необходимо установление некоторой схемы компромисса – принципа согласования оптимумов по разным критериям.
Число возможных схем компромисса очень велико, но во всех случаях задача метода – это сведение векторной задачи оптимизации к эквивалентной (в смысле принятого принципа оптимальности) скалярной (т.е. однокритериальной) задаче.
Различные схемы компромисса, в первую очередь, могут отличаться по наличию или отсутствию приоритетов в достижении локальных целей.
Оценка значимости целей
В том случае, когда достижение отдельных целей предпочтительнее достижения других, то для оценки степени предпочтительности вводятся приоритеты. Приоритет локальных критериев может задаваться различными способами. Наибольшее распространение получил способ, который состоит в задании весовых коэффициентов для каждого локального критерия – aj(j = 1..n).
Следовательно, каждому критерию (цели) по степени важности присваивается весовой коэффициент, соответственно:
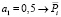 ,
,
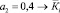 ,
,
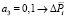 .
.
Производится оценка важности каждой цели определенным числом аj так, чтобы для более важной цели аj было больше, чем для менее важной:
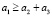 , (4)
, (4)
Так как 0,5 ≥ 0,4 + 0,1, 0,5 ≥ 0,5, следовательно, условие неравенства (4) целей выполняется.
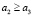 , (5)
, (5)
Так как 0,4 ≥ 0,1, следовательно, весовым коэффициентам корректировки не требуется.
Результаты исследования представлены в табл. 3.
По максимальной эффективности предложенные варианты можно ранжировать в порядке возрастания: φ 5, φ 2, φ 3, φ1, φ 4, φ 6.
В качестве оптимального варианты (стратегии) принимается вариант, у которого оценка общей эффективности максимальна:
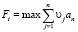 . (6)
. (6)
где νj – нормированные значения критериев,
an – весовой коэффициент.
Таблица 3
Матрица нормированных критериев
|
Стратегии |
|
|
|
Интегральный критерий
|
|
а1 = 0,5 |
а2 = 0,4 |
а3 = 0,1 |
||
|
φ1 |
0,16 |
0,4 |
0,012 |
0,572 |
|
φ2 |
0,265 |
0,292 |
0,013 |
0,57 |
|
φ3 |
0,25 |
0,296 |
0,025 |
0,571 |
|
φ4 |
0,355 |
0,34 |
0,026 |
0,721 |
|
φ5 |
0,485 |
0,172 |
0,026 |
0,198 |
|
φ6 |
0,5 |
0,212 |
0,1 |
0,812 |
Таблица 4
Матрица нормированных критериев
|
Стратегии |
|
|
|
Интегральный критерий
|
|
а1 = 0,4 |
а2 = 0,5 |
а3 = 0,1 |
||
|
φ1 |
0,128 |
0,5 |
0,012 |
0,64 |
|
φ2 |
0,212 |
0,365 |
0,013 |
0,378 |
|
φ3 |
0,2 |
0,37 |
0,025 |
0,595 |
|
φ4 |
0,284 |
0,425 |
0,026 |
0,451 |
|
φ5 |
0,388 |
0,215 |
0,026 |
0,629 |
|
φ6 |
0,4 |
0,265 |
0,1 |
0,765 |
Следовательно, при заданных приоритетах, оптимальным считается шестой вариант:
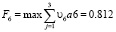 о.е.
о.е.
В том случае, если больший приоритет присваивается такому критерию как капитальные вложения, то весовые коэффициенты будут распределены следующим образом: а1 = 0,4, а2 = 0,5, а3 = 0,1.
Результаты данного исследования сведены в табл. 4.
Порядок возрастания по максимальной эффективности предложенных вариантов изменится: φ2 , φ 4, φ 3, φ 5, φ1, φ6. Оптимальным остается шестой вариант.
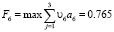 о.е.
о.е.
Изложенный метод может использоваться при исследовании вариантов новых технических решений в условиях недостаточности информации.
Выводы
Предложен алгоритм выбора оптимального решения по многокритериальной модели, позволяющий получить обоснованное решение поставленной задачи. Данную методику предлагается использовать в учебных целях для подготовки специалистов энергетических специальностей.


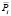 , о.е.
, о.е.
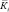 , о.е.
, о.е.
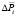 , о.е.
, о.е.
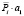 , о.е.
, о.е.
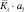 , о.е.
, о.е.
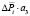 , о.е.
, о.е.
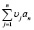
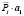 , о.е.
, о.е.
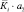 , о.е.
, о.е.
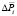 , о.е.
, о.е.