Специфика вида спорта предъявляет к спортсмену те отличительные анатомические, физиологические и функциональные признаки, физические качества и двигательные способности, наличие которых будет способствовать его успешной спортивной карьере. Как отмечает А.Ю. Бокин [2], по мнению ряда ведущих специалистов В.Л. Ботяева, З. Витковски, А.С. Жукова, Н.Л. Журавина, Л.П. Матвеева, А.М. Пидоря и других, наибольшее значение в подготовке квалифицированных спортсменов имеет развитие физических качеств, которые влияют на техническую сторону выполнения соревновательного упражнения и сам спортивный результат. В их исследованиях установлено, что с ростом спортивной квалификации точность выполнения упражнений, их быстрота, прочность овладения двигательными навыками все теснее коррелируют с уровнем спортивных результатов.
Единоборства требуют от спортсмена кроме хорошей физической подготовленности еще и быстроты реакции, высокой скорости принятия решений, устойчивости внимания, высокого уровня функциональных возможностей нервной системы [9]. При этом точность движений, по мнению К.В. Курносова [3], приобретает все большое значение, что в значительной мере обусловлено исчерпанием ресурсов повышения эффективности двигательных действий за счет быстроты, силы и выносливости.
Для тестирования быстроты и точности двигательных действий используется большое количество тестов, среди которых выделяются, как считает И.А. Петров [6], сравнение результатов челночного бега 3×10 м и бега на 30 м, теппинг-тест и точность реакции на движущийся объект (РДО). Вопросы тестирования РДО рассмотрены в работах [1, 5], использования теста РДО при отборе для занятий игровыми видами спорта в работе [8].
Цель работы – разработка методики спортивного отбора для занятий единоборствами.
Материалы и методы исследования
Испытуемым предъявляли на экране видеомонитора окружность, на которой помещена метка 1 и точечный объект 2, движущийся с заданной скоростью по окружности, как показано на рис. 1.
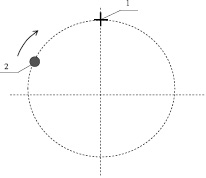
Рис. 1. Схема тестирования реакции на движущийся объект
Испытуемые, наблюдая за движением точечного объекта 2, в момент предполагаемого совпадения положения движущегося точечного объекта 2 с меткой 1 нажатием кнопки «Стоп» останавливали движение точечного объекта 2 по окружности. После останова компьютер вычислял ошибку не совпадения точечного объекта 2 и метки 1 – время ошибки запаздывания с положительным знаком, мс или упреждения с отрицательным знаком, мс и через заданное время, равное 1 секунде, возобновлял движение точечного объекта 2 по окружности.
Испытуемые выполняли описанную процедуру 13 раз, 3 начальных результата из анализа исключались, как принято в [7]. После этого строили вариационный ряд ошибок не совпадения точечного объекта 2 и метки 1, вычисляли вариационный размах ряда по формуле:
R = tmax–tmin,
где tmax и tmin – соответственно наибольший и наименьший члены вариационного ряда, и отмечали на числовой оси отрезок, ограниченный наибольшим и наименьшим членами вариационного ряда.
Отбор выполняли по расположению на числовой оси отрезка, ограниченного наибольшим и наименьшим членами вариационного ряда ошибок не совпадения точечного объекта 2 и метки 1, наиболее сдвинутом в область отрицательных значений, и меньшему значению вариационного размаха ошибок не совпадения точечного объекта 2 и метки 1 [4].
Результаты исследования и их обсуждение
В обследовании участвовало 15 испытуемых, подростков 9–10 лет, занимающихся в ДЮСШ. Так в результате тестирования подростка У., 10 лет, получены следующие значения ошибок не совпадения положений точечного объекта и метки в мс: – 15, – 32, 8, – 32, – 46, – 17, – 39, – 29, – 8, 5, представленные в виде диаграммы на рис. 2.
Наибольший член вариационного ряда ошибок не совпадения точечного объекта и метки равен 8 мс, наименьший член вариационного ряда – минус 46 мс, вариационный размах – 54 мс. Расположение на числовой оси отрезка, ограниченного наибольшим и наименьшим членами вариационного ряда ошибок не совпадения точечного объекта и метки, представлено на рис. 5, а.
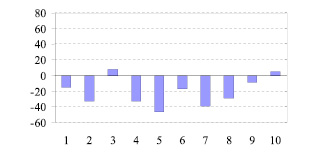
Рис. 2. Диаграмма значений ошибок не совпадения точечного объекта и метки подростка У. По горизонтальной оси – номер измерения, по вертикальной оси – ошибка не совпадения положений точечного объекта и метки, мс
В результате тестирования подростка Ч., 9 лет, получены следующие значения ошибок не совпадения положений точечного объекта и метки в мс: – 10, – 36, 15, – 11, – 9, – 11, 18, 25, – 18, – 20, представленные в виде диаграммы на рис. 3.
Наибольший член вариационного ряда ошибок не совпадения точечного объекта и метки равен 25 мс, наименьший член вариационного ряда – минус 36 мс, вариационный размах – 61 мс. Расположение на числовой оси отрезка, ограниченного наибольшим и наименьшим членами вариационного ряда ошибок не совпадения точечного объекта и метки, представлено на рис. 5, б.
В результате тестирования подростка Ш., 9 лет, получены следующие значения ошибок не совпадения положений точечного объекта и метки в мс: – 13, – 9, 12, 26, – 6, – 8, 33, 45, 50, 65, представленные в виде диаграммы на рис. 4.
Наибольший член вариационного ряда ошибок не совпадения точечного объекта и метки равен 65 мс, наименьший член вариационного ряда – минус 13 мс, вариационный размах – 78 мс. Расположение на числовой оси отрезка, ограниченного наибольшим и наименьшим членами вариационного ряда ошибок не совпадения точечного объекта и метки, представлено на рис. 5, в.
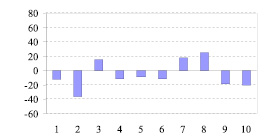
Рис. 3. Диаграмма значений ошибок не совпадения точечного объекта и метки подростка Ч. По горизонтальной оси – номер измерения, по вертикальной оси – ошибка не совпадения положений точечного объекта и метки, мс
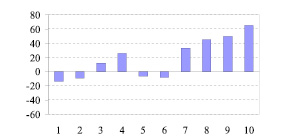
Рис. 4. Диаграмма значений ошибок не совпадения точечного объекта и метки подростка Ш. По горизонтальной оси – номер измерения, по вертикальной оси – ошибка не совпадения положений точечного объекта и метки, мс
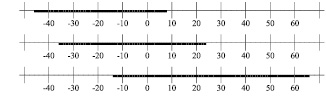
Рис. 5. Расположение на числовой оси результатов тестирования испытуемых
Анализ результатов тестирования испытуемых свидетельствует, что расположение на числовой оси отрезка, ограниченного наибольшим и наименьшим членами вариационного ряда ошибок не совпадения точечного объекта и метки, наиболее сдвинуто в область отрицательных значений у испытуемого У., следовательно, быстрота его двигательных действиях выше, чем у испытуемых Ч. и Ш.
Вариационный размах ошибок не совпадения точечного объекта и метки у испытуемого У. наименьший, следовательно, точность его двигательных действиях выше, чем у испытуемых Ч. и Ш.
По результатам анализа результатов тестирования из обследованной группы двум подросткам, в том числе подростку У., рекомендованы занятия единоборствами.
Заключение
Разработана методики спортивного отбора для занятий единоборствами, основанная на анализе результатов тестирования реакции на движущийся объект. Методика апробирована на группе из 15 испытуемых, подростков 9–10 лет, занимающихся в ДЮСШ. По результатам тестирования двум подросткам рекомендованы занятия единоборствами. Методика может быть использована как для первичного отбора, так и для оценки качества тренированности и комплектации команды высококвалифицированных спортсменов.

