Считается установленным, что на качество обработки поверхностным пластическим деформированием определяется интенсивностью и законом определения контактных напряжений между деформирующим элементом и обрабатываемой поверхностью [1, 2, 3].
В ряде литературных источников указывается на возможность применения для описания упругопластической задачи, хорошо зарекомендовавшего себя на практике метода определения напряженного состояния при упругом сближении тел под воздействием нормально действующих нагрузок [3]. При этом полагают, что максимальные напряжения в наиболее нагруженной точке контактной зоны превышают предел упругости. Величина максимального напряжения по разным источникам [2] может превышать предел упругости от 2 до 12 раз. В связи с большим расхождением во мнениях о величине максимального напряжения, в каждом конкретном случае теоретические разработки необходимо подтверждать экспериментальными исследованиями. Еще одной особенностью применения упругой контактной задачи является то, что она применима для ограниченного количества деформируемых тел: шаров, цилиндров, плоскостей и поверхностей, имеющих произвольную кривизну, которые первоначально при отсутствии нагрузки соприкасаются в точке. Формы контурных линий контактов при деформировании указанными телами представляют собой эллипсы и прямоугольники.
Для других форм контактов, в частности, каплевидного, часто применяющегося в производственной практике при ППД коническими роликами, задача вообще не решена. Идея достижения требуемого результата определения напряжений для произвольных контактов заключается в том, чтобы перенести решение упругой задачи при контактировании двух деформируемых цилиндров с параллельными осями, дающих прямоугольный контакт, на решение задачи, когда форма контакта является более сложной.
Для одной и той же силы, приложенной к деформирующему ролику, максимальные напряжения и закон распределения по ширине контакта могут принимать самые различные значения. Если принять, что закон распределения по ширине контакта известен, то известным будет и максимальное напряжение в центре контакта. При деформировании поверхности роликом произвольной конфигурации, отличающейся от форм, для которых задача уже решена, остается неизвестным закон распределения максимальных напряжений вдоль ролика по линии его максимального нагружения.
В работе было установлено, что решения контактной задачи по Герцу и для упругопластического контакта с применением связи деформаций с перемещениями и напряжениями отличаются не более чем на 10 %. Так как исследования контактной зоны определяются в статике, то в качестве исходной информации для дальнейших исследований примем решение задачи для деформирования плоскости валом (рис. 1).
Распределение напряжений по площади контакта в этом случае определяется по формуле:
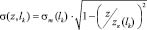, (1)
где z – текущая координата полуширины контакта (0 ≤ z ≤ zk(lk)); zk(lk) – изменение полуширины контакта по его длине; σт(lk) – изменение напряжений по линии максимального нагружения ролика.
Разобьем тело ролика по длине контакта параллельными плоскостями, расположенными перпендикулярно его оси, на расстоянии Δlk друг от друга. Таким образом, весь ролик будет состоять как бы из набора тонких дисков, имеющих постоянные радиусы, которые меняются для каждого выделенного диска по длине ролика в соответствии с законом изменения его образующей. Для каждого из этих дисков применим формулу (5.20) для расчета напряжений по ширине контакта. Очевидно, напряженное состояние на всей площади контакта будет складываться из суммы элементарных решений для каждого диска в отдельности. Для того чтобы иметь возможность пользоваться формулой (5.20), необходимо определить закон изменения максимальных напряжений σт(lk) по линии наибольшего нагружения ролика.
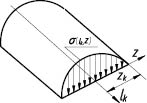
Рис. 1. Распределение напряжений по площади полосового контакта при деформировании плоскости цилиндрическим телом
Это линия, вдоль которой ролик максимально внедрен в поверхность обрабатываемой детали. При упругом контакте данная зависимость при внедрении вала единичной длины в плоскость может быть записана в виде выражения
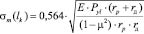, (2)
где
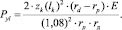(3)
Для нахождения экспериментального закона изменения функции σт(lk) возможны два подхода.
Первый из них сводится к тому, чтобы на основе априорных соображений предложить подходящую зависимость, а затем подтвердить ее экспериментально. Предположим, что удалось найти искомую функцию σт(lk). Тогда для полного усилия деформирования можно записать выражение:
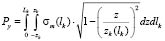. (4)
Если определить экспериментально значения усилия деформирования Py, изменение полуширины контакта zk(lk), длину контактной зоны Lk и подставить их в приведенную зависимость, то при правильно выбранной формуле изменения максимального напряжения σт(lk) по линии наибольшего внедрения ролика, написанное равенство должно превратиться в тождество.
При другом подходе экспериментально определяют максимальное напряжение для каждого тонкого диска, при разных радиусах и глубинах внедрения, по специально разработанной методике.
Схема компоновки экспериментальной установки показана на рис. 2.
На основании 7 закреплена подставка 6, в которой устанавливается исследуемый образец 3, (валик или сегмент втулки). Деформирующий ролик 1, имеющий выступающий в средней части буртик толщиной 3 мм с изменяемым для каждого отдельного измерения радиусом, вдавливается в поверхность образца силой Р. Ролик устанавливается в накладке 2 по плотной посадке. Индикатором часового типа с ценой деления 1 мкм измеряется глубина внедрения ролика, из которой вычитается рассчитанная по теоретическим зависимостям деформация ролика.
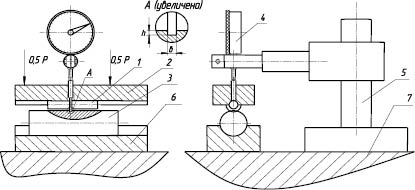Рис. 2. Схема экспериментального исследования распределения напряжений по линии максимального нагружения: 1 – деформирующий ролик с пояском, 2 – накладка, 3 – исследуемый образец, 4 – индикатор часового типа с ценой деления 0,001 мм, 5 – штатив, 6 – подставка для образца, 7 – основание
Предполагая известным закон изменения напряжений по ширине контакта σz(z), определяют максимальные напряжения по формуле
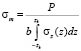(5)
где b – ширина диска; zk – полуширина контакта, рассчитываемая по определенной в эксперименте глубине внедрения ролика из зависимости
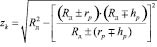, (6)
где знак + применяется при внедрении образца с радиусом rp в поверхность вала, а знак – при внедрении образца в поверхность отверстия.
Определив, таким образом, максимальное напряжение для каждого значения радиуса диска, выбранного из заданного интервала его изменения, строят зависимость σm(r, h).