Цилиндрические зубчатые передачи имеют большое распространение в различных приводах машин. От качества их изготовления и сборки зависит долговечность и надежность передач, в которых они применяются. Основным параметром, существенно влияющим на выносливость рабочих поверхностей зубьев являются контактные напряжения между рабочими поверхностями зубьев. При расчетах зубчатого прямозубого зацепления контактные напряжения рассчитывают по их наибольшим значениям на основе использования формулы Герца, которая справедлива при контактировании двух произвольных цилиндров расположенных параллельных друг другу (рис. 1).
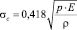, (1)
где σс – наибольшее контактное напряжение сжатия; р – удельная контактная нагрузка; Е- модуль упругости материала поверхностных слоев соприкасающихся тел; ρ – приведенный радиус кривизны соприкасаемых рабочих поверхностей (1/ρ = 1/ρ1 + 1/ρ2), ρ1, ρ2 – радиусы кривизны контактируемых тел соответственно.
При параллельном расположении осей валов радиусы кривизны определяются по формуле:
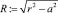(2)
где r – радиус делительной окружности, a – радиус основной окружности (рис. 1).
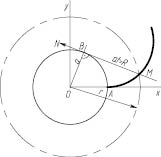
Рис. 1. Отрезок МВ производящей прямой есть радиус кривизны эвольвенты в точке М
Однако за счет погрешностей имеющих место при изготовлении и сборке возникает перекос осей валов, на которых установлены зубчатые колеса. Это приводит к тому, что полосовой первоначальный контакт между поверхностями зубьев при перекосе поверхностей зубьев преобразуется в эллипсный контакт. Геометрические параметры этого контакта могут быть определены на основе формул применяющихся в расчетах при упругом деформировании двух тел двояковыпуклой кривизны. На рис. 2 показана схема контакта двух зубьев повернутых друг относительно друга на углы γ1 и γ2. Значения этих углов могут быть определены на основании выявления и решения разменных угловых цепей сборочного узла цилиндрического зубчатого соединения. Методика выявления и решения этих размерных цепей приведена в [1] и показана на рис. 2. В сечениях А-А и Б-Б образуются кривые, имеющие эквивалентные радиусы R12, R22.
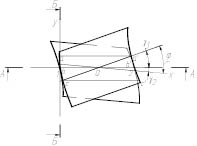
Рис. 2. Схема для определения радиусов кривизны при непараллельности осей
Алгоритм расчета радиусов кривизны при перекосе валов
Рассмотрим сечение А – А:
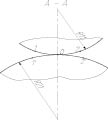
Рис. 3. Сечение А – А
На рис. 3 R11 и R21 – радиусы окружностей, проходящих через три заданные точки (на рис. 2 т. 1, 2, 3). Определяются по формулам:
, 
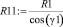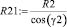(3)
γ1 и γ2 – углы перекосов соответственно первого и второго колес.
R1 и R2 определены выше.
Рассмотрим сечение Б – Б:
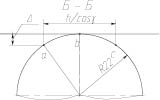
Рис. 4. Сечение Б – Б
При построении сечения предполагалось, что при перекосе валов, рассматривая сечение Б – Б радиус второй эквивалентной окружности будет стремиться к бесконечности, следовательно, эквивалентная окружность преобразуется в прямую.
На рис. 4 R22 – радиус эквивалентной окружности в точке касания зубчатых колес при перекосе валов. Алгоритм определения данного радиуса приведен ниже:
,
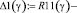
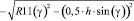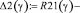
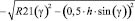(4)
h – ширина зубчатого венца.
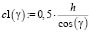
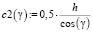(5)
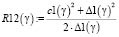
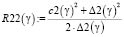(6)
Согласно методике определения геометрических параметров контакта при деформировании тел двояковыпуклой кривизны [2] полуоси эллипсного контакта определяются по следующему алгоритму:
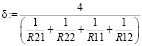(7)
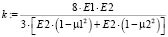(8)
Е1, Е2 – модули упругости материалов зубчатых колес,
μ1, μ2 – коэффициенты Пуассона
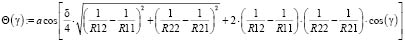(9)
, 
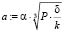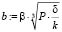(10)
a и b – наименьшая и наибольшая полуоси эллипса соответственно.
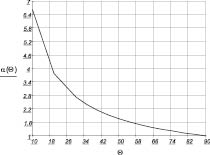
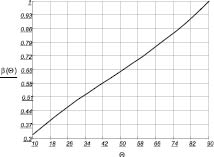
Рис. 5. Значения α, β в зависимости от угла θ, где α, β выбираются в зависимости от значения θ, град
Зная геометрические параметры пятна контакта, можно определить максимальное давление, действующее в точке контакта:
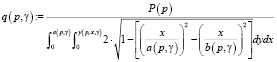. (11)
В ходе выполнения расчетов были выведены следующие закономерности:
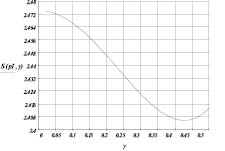
Рис. 6. Зависимость площади контакта от угла перекоса
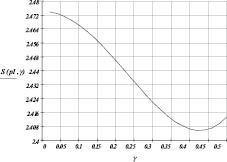
Рис. 7. Отношение максимального напряжения площади контакта
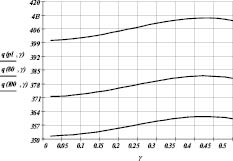
Рис. 8. Зависимость наибольшего давления по эллиптической площадке контакта от угла перекоса