Для успешного управления технологическими процессами и их оптимизации уже недостаточно знания отдельных качественных сторон процесса. Для анализа сложных технологических процессов широко применяются методы технической кибернетики. Техническая кибернетика, получающая в настоящее время все большее развитие в текстильной промышленности, – это прикладная наука, изучающая способы управления сложными технологическими системами, т.е. процессами и машинами, с помощью средств, разработанных теоретической кибернетикой. К числу этих средств, в первую очередь, относятся методы математического моделирования технологических процессов, которые включают методы получения математических моделей и их исследование с помощью электронных вычислительных машин.
В данной работе проводилось математическое моделирование технологии выработки хлопчатобумажной ткани бязь с использованием метода приближения функции по Фурье и анализа характера протекания технологического процесса ткачества.
Обрывность нитей в ткачестве является одним из важных показателей уровня технологии и организации производства. Одним из основных факторов, влияющих не уровень обрывности нитей, является их натяжение.
С помощью математических моделей появляется возможность осуществлять мониторинг технологического процесса и таким образом влиять на качество продукции.
Анализ ранее проведенных исследований показал, что проблеме математического моделирования натяжения нитей основы уделялось и уделяется достаточно много внимания. Если раньше эти модели являлись, в основном, результатом проведения факторных экспериментов и для их получения требовалось не только высокая квалификация экспериментатора, но и значительные материальные и временные затраты для их получения, то в настоящее время разработаны эффективные методики получения математических моделей на основе численных методов моделирования технологических процессов ткацкого производства [1, 6, 7].
Для разработки математической модели технологического процесса выработки хлопчатобумажной ткани бязь предлагается использовать один из самых распространенный методов приближения функций – тригонометрический полином Фурье.
Объектом исследования является ткацкий станок СТБ-2-216, на котором вырабатывалась ткань бязь арт. 262.
Для решения задачи, заключающейся в разработке метода получения математической модели, эффективно описывающей натяжение нитей основы на ткацком станке, выбрана ткань бязь арт. 262, выработка которой осуществляется на ткацком станке СТБ-2-216. Краткая техническая характеристика ткани бязь арт. 262 представлена в табл. 1.
Для получения значений натяжения нитей различного сырьевого состава при переработке их на ткацком станке СТБ-2-216 используем тензометрическую установку «ТТП-2008», разработанную в Камышинском технологическом институте и предназначенную для измерения натяжения группы движущихся нитей.
Таблица 1
Краткая техническая характеристика хлопчатобумажной ткани бязь арт. 262
|
Параметры ткани |
Значение |
|
Плотность ткани по основе Ро, нитей/см |
20 |
|
Плотность ткани по утку Ру, нитей/см |
10 |
|
Линейная плотность по основе То, текс |
29 |
|
Линейная плотность по утку Ту, текс |
29 |
|
Заправочная ширина, см |
216 |
Для реализации поставленной задачи по разработке математической модели технологического процесса выработки хлопчатобумажной ткани бязь в лаборатории ткачества кафедры «Технология текстильного производства» на станке СТБ-2-216 в зоне «скало-ламельный прибор» был установлен тестер натяжения «ТТП – 2008», схема установки которого представлена на рис. 1.
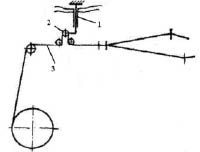
Рис. 1. Схема установки прибора для измерения натяжения основных нитей за цикл работы ткацкого станка (1 – тестер натяжения, 2 – воспринимающий упругий элемент (балочка), 3 – нити основы)
В результате проведенных измерений были получены тензограммы, отражающие изменение натяжения основных нитей за один оборот главного вала станка. На рис. 2 представлена одна из полученных тензограмм натяжения нитей основы от угла поворота главного вала ткацкого станка СТБ-2-216 при выработке хлопчатобумажной ткани бязь.
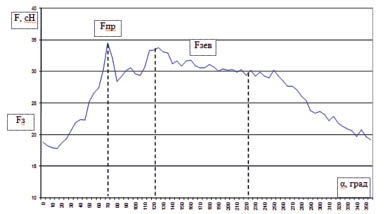
Рис. 2. Диаграмма изменения натяжения нитей основы на ткацком станке СТБ-2-216 при выработке ткани бязь (Fз – заправочное натяжение нитей основы, сН; Fпр – натяжение нитей во время прибоя уточной нити к опушке ткани, сН; Fзев – натяжение нитей во время зевообразования, сН)
Для математического описания технологических процессов ткацкого производства был использован алгоритм применения тригонометрического полинома Фурье [2]:
1. На технологическом оборудовании, установленном в ткацком производстве или в лабораторных условиях, с помощью контрольно-измерительных приборов получаем тензограмму натяжения нитей. На ней выделяем участок, после которого цикл натяжения нитей повторяется.
2. Для получения дискретной информации об исследуемом процессе разбиваем тензограмму натяжения нитей на 11 частей, получаем значения натяжения нитей в каждой точке разбиения и заносим в табл. 2.
3. Для приближенного представления функции в виде многочлена Фурье определяем следующие коэффициенты:
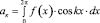
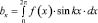
4. Для вычисления интегралов применяется одна из формул для численного интегрирования, обычно самая простая из них – формула прямоугольников. Интеграл делится на n-равныx частей с помощью точек X0, X1, X2 ... Xn-1, Xn = 2p.
Тогда
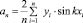
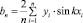 ,
,
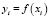 .
.
5. Принимая во внимание особенности множителей, cos kxi и sin kxi берут равным 12. При этом каждое из 12 учитываемых значений функции умножается лишь на одно из следующих чисел:
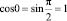 ,
, 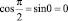 ,
,
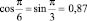 ,
, 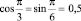 .
.
6. Для вычисления коэффициентов регрессионного уравнения используются следующие формулы:
a0 = Σ yi /6
a1 = y0 + y1·0,87 + y2·0,5 – y4·0,5 – y5·0,87 – y6 – y7·0,87 – y8·0,5 + y10·0,5 + y11·0,87
b1 = y1·0,5 + y2·0,87 + y3 + y4·0,87 + y5 ·0,5 – y7·0,5 – y8·0,87 – y9 – y10·0,87 – y11·0,5
a2 = y0 + y1·0,5 – y2·0,5 – y3 – y4·0,5 + y5·0,5 + y6 + y7·0,5 – y8·0,5 – y9 – y10·0,5 + y11·0,5
b2 = y1·0,87 + y2·0,87 – y4·0,87 – y5·0,87 + y7·0,87 + y8·0,87 – y10·0,87 – y11·0,87
a3 = y0 – y2 + y4 – y6 + y8 – y10
b3 = y1 – y3 + y5 – y7 + y9 – y11
a4 = y0 + y3 + y6 + y9
b4 = y1·0,87 – y2·0,87 + y4·0,87 – y5·0,87 + y7·0,87 – y8·0,87 + y10·0,87 – y11·0,87
a5 = y0 – y1·0,87 + y2·0,5 – y4·0,5 + y5·0,87 – y6 + y7·0,87 – y8·0,5 + y10·0,5 – y11·0,87
b5 = y1·0,5 – y2·0,87 + y3 – y4·0,87 + y5·0,5 – y7·0,5 + y8·0,87 – y9 + y10·0,87 – y11·0,5
a6 = y0 – y1 + y2 – y3 + y4 – y5 + y6 – y7 + y8 – y9 + y10 – y11
Таблица 2
Экспериментальные данные натяжения нитей
|
Точки разбиения интервала |
Значения функции натяжения нитей основы |
|
|
yi |
Натуральные значения, сН |
|
|
0 |
y0 |
39 |
|
1 |
y1 |
27,9 |
|
2 |
y2 |
18,7 |
|
3 |
y3 |
18,7 |
|
4 |
y4 |
19 |
|
5 |
y5 |
20 |
|
6 |
y6 |
20 |
|
7 |
y7 |
13 |
|
8 |
y8 |
16,7 |
|
9 |
y9 |
19 |
|
10 |
y10 |
22 |
|
11 |
y11 |
32 |
7. Подставляем полученные коэффициенты в регрессионное уравнение, общий вид которого имеет следующий вид:
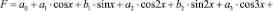
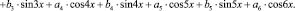
Таким образом, получаем приближенное выражение функции изменения натяжения нити во времени в виде тригонометрического полинома Фурье.
По данному алгоритму с использованием автоматизированного метода расчета в среде программирования MathCad [2], была получена математическая модель технологического процесса выработки хлопчатобумажной ткани бязь.
Для определения характера протекания технологического процесса выработки хлопчатобумажной ткани бязь в работе определялась повреждаемость нитей основы по критерию длительной прочности Москвитина [3, 4, 5]. Установлено, что данный критерий дает более точные результаты, так как учитывает предысторию нагружения нитей.
Согласно критерию Москвитина, коэффициент повреждаемости нитей основы можно рассчитать по следующей формуле:
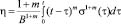 .
.
где m – коэффициент, учитывающий предысторию нагружения; t – время разрушения; s – напряжение нити.
Результаты расчетов значений коэффициентов повреждаемости основных нитей за один цикл нагружения (один оборот главного вала ткацкого станка), рассчитанных на основе реального закона нагружения нитей, сведены в табл. 3.
Многочисленными исследованиями показано, что:
1) при η < 0,25 – процесс протекает в спокойных условиях
2) при η = 0,25 – 0,5 – процесс проходит в довольно напряженных условиях;
3) при η = 0,5 – 0,75 – процесс возможен, но наблюдается повышенная обрывность нитей (примерно в 2 раза);
4) при η = 0,75 – 1 – процесс возможен, но резко увеличивается обрывность нитей (примерно в 5 раз);
5) при η > 1 – процесс практически невозможен.
Из табл. 3 видно, что наибольшую повреждаемость имеют нити основы в процессе прибоя.
Таким образом, в результате проведенных исследований было установлено, что исследуемая ткань, вырабатывается в довольно напряженных условиях, вследствие чего на ткацком станке пряжа в данных технологических условиях перерабатывается с повышенной обрывностью нитей.
Поэтому необходимо пересмотреть технологический процесс ткачества и установить такой оптимальный режим, где повреждаемость нитей будет минимальной. Причем рекомендуется в качестве критерия оптимизации использовать коэффициент повреждаемости нитей основы, полученный на основе расчета критерия длительной прочности Москвитина с использованием предложенного в данной работе автоматизированного метода расчета повреждаемости нитей.
Таблица 3
Значения коэффициента повреждаемости основных нитей за один оборот главного вала станка
|
Наименование ткани |
Fз, сН |
Fпр, сН |
Fзев, сН |
Т, текс |
h |
Среднеквадратическая ошибка |
|
Бязь |
14 |
39 |
21,5 |
29 |
0,373 |
0,065 |
Выводы
1. Проведен анализ работ, посвященных математическому моделированию технологических процессов ткацкого производства.
2. Проведен анализ работ, посвященных разработке алгоритмов автоматизированных методов получения математических моделей в ткацком производстве.
3. Проведен эксперимент по исследованию технологического процесса выработки хлопчатобумажной ткани бязь.
4. Получена математическая модель, описывающая изменение натяжения нитей основы на ткацком станке СТБ-2-216 при выработке хлопчатобумажной ткани бязь.
5. Определена повреждаемость нитей основы в различные моменты тканеформирования с использованием критерия длительной прочности Москвитина.

