Современный мир практически невозможно представить без технических систем, ставших неотъемлемой частью как повседневной жизни и профессиональной деятельности человека, так и ключевыми элементами различных предприятий и отраслей экономики. Помимо функциональных возможностей и основных технических характеристик, которые в первую очередь интересуют конечных потребителей и производителей, таких как: производительность, мощность, емкость и т.п., не менее важными являются показатели надежности, так как от них напрямую зависит эффективность и безопасность эксплуатации технических систем. Соответственно, разработка моделей и методов для расчета показателей надежности систем является актуальной и критически важной задачей.
На сегодняшний день имеется множество учебников [1, 2, 3], посвященных основам теории надежности, общим и специализированным моделям и методам расчета показателей надежности систем. Одной из самых распространенных моделей восстанавливаемых технических систем является модель на базе цепей Маркова, позволяющих оценить такие показатели надежности системы как: коэффициент готовности, среднее время наработки на отказ, среднее время восстановления. В случае если система состоит из нескольких идентичных элементов, например: отказоустойчивые дисковые массивы хранения данных, высокопроизводительные вычислительные системы, гомогенные сети передачи данных, то в таком случае применяется хорошо известная марковская цепь гибели и размножения.
Однако следует особо отметить, что существуют системы, которые при достижении аварийного состояния не могут вернуться в предыдущее работоспособное состояние после замены минимально необходимого одного элемента, и требуют проведения ремонтных работ до исходного полностью исправного состояния. Примером таких систем являются дисковые системы RAID (избыточный массив недорогих дисков), состоящий из n дисков, устойчивый к отказам до s – 1 дисков, и отказывающий вместе с потерей всех данных при отказе s и более дисков, и требующий пересоздания массива «с нуля» и восстановления данных из резервной копии. Для таких систем традиционная модель гибели и размножения не совсем подходит, и требуется модифицированная модель.
В последние годы автором статьи был проведен ряд исследований в области надежности современных систем хранения, передачи и обработки данных [4–10], состоящих из нескольких идентичных элементов. Соответственно, при работе с системами, требующими ремонта до исходного полностью исправного состояния после достижения состояния отказа, возникла научная задача разработки подходящей модели надежности для заданного количества элементов и заданного порога отказа.
В рамках данной статьи рассматриваются предложенная автором марковская цепь гибели и размножения с петлевой связью и выведенные формулы для расчета показателей надежности системы, состоящей из n идентичных восстанавливаемых элементов, переходящей в состояние отказа с аварийным отключением при отказе s элементов и требующей проведения ремонта до исходного полностью исправного состояния. Также рассматривается частный случай модели и пример расчета показателей надежности.
Обобщенная модель системы на базе цепи Маркова. Пусть имеется система с n идентичными восстанавливаемыми элементами и произвольной зависимостью по отказам и восстановлениям, причем система сохраняет работоспособность при отказе не более s – 1 элементов, 1 ≤ s ≤ n. Пусть при достижении состояния s система аварийно отключается, и оставшиеся работоспособные элементы не могут отказывать.
Кроме того, пусть после аварийного отключения требуется ремонт, возвращающий систему в исходное полностью исправное состояние 0. Интенсивность полного восстановления задается параметром γ.
Рассмотрим следующую обобщенную модель надежности системы на базе марковской цепи гибели и размножения с петлевой связью (рис. 1).
Соответственно, математическая модель (система уравнений Колмогорова-Чепмена):
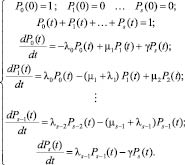
Стационарные вероятности при t → ∞ могут быть получены путем решения системы уравнений с учетом того, что в бесконечной перспективе марковский процесс становится установившимся, и производные стремятся к нулю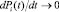 
. Это существенно упрощает решение системы. Автором была выведена следующая формула для стационарных вероятностей всех состояний системы:
;
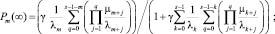
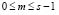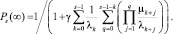(1)
Тогда, стационарный коэффициент готовности такой системы:
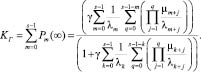(2)
Рис. 1. Обобщенная модель надежности системы
Среднее время восстановления системы – это есть среднее время перехода из аварийного состояния s в начальное состояние 0, и оно зависит только от интенсивности полного восстановления γ системы, поскольку из аварийного состояния системы может перейти лишь только в начальное состояние:
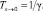(3)
Среднее время наработки на отказ – это есть среднее время перехода из начального состояния 0 (при запуске системы в начальный момент времени или после очередного полного восстановления системы) в аварийное состояние s. Учитывая, что среднее время полного восстановления равно 1/γ, и используя тождество, связывающее коэффициент готовности средними временами KГ = Т0→s/(Т0→s + Тs→0), получаем формулу для среднего времени наработки на отказ системы:
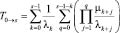. (4)
Особо отметим, что среднее время наработки на отказ рассматриваемой системы совпадает со средним времени наработки до первого отказа.
Специализированный частный случай модели системы. Пусть имеется некоторая система, состоящая из n идентичных элементов с интенсивностью отказов λ и интенсивностью восстановления μ, сохраняющая работоспособность при отказе до s – 1 элементов. При этом оставшиеся работоспособные элементы испытывают дополнительную нагрузку, и к интенсивности отказов добавляется дополнительная интенсивность ε.
Пусть при отказе s элементов система аварийно отключается, и после этого требуется восстановительная работа, которая выполняется с интенсивностью γ, и приводит систему в исходное полностью исправное состояние 0.
Пусть имеются несколько ремонтных бригад, позволяющих одновременно восстанавливать до r отказавших элементов.
Тогда модель надежности системы (рис. 2) является частным случаем рассмотренной выше модели с интенсивностями переходов, λ0 = nλ; λi = (n – i)(λ + ε); i = 1…s – 1 и μj = μ∙min(j, r); j = 1…s – 1 и γ:
Рис. 2. Специализированная модель надежности системы
Соответственно, стационарный коэффициент готовности рассматриваемой системы:
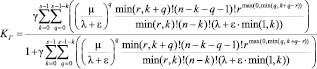. (5)
Среднее время наработки на отказ:
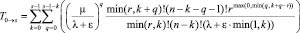. (6)
Среднее время восстановления системы:
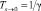. (7)
Пример расчета показателей надежности. Имеется избыточный дисковый массив, состоящий из n = 8 дисков и сохраняющий работоспособность при отказе не более двух дисков. Интенсивность отказов дисков λ = 1/120000 час-1. После отказа и замены дисков, массив начинает процесс реконструкции информации на замененных дисках за счет информации оставшихся дисков, и к интенсивности отказов оставшихся дисков добавляется интенсивность ε = 1/300 час-1. Интенсивность восстановления дисков (включая замену и реконструкцию информации на них) составляет μ = 1/24 час-1. Одновременно могут восстанавливаться до r = 2 дисков. При отказе s = 3 дисков массив аварийно отключается, и все данные теряются, и выполняется замена отказавших дисков, полная реконструкция массива и копирование данных из резервного хранилища с интенсивностью γ = 1/72 час-1.
Рассчитать показатели надежности массива RAID-6 с резервной копией данных.
Решение. Граф состояний для рассматриваемой задачи (рис. 3):
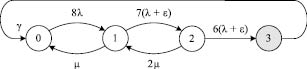
Рис. 3. Модель надежности дискового массива с резервной копией данных
Соответственно, стационарный коэффициент готовности:
.
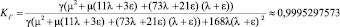Среднее время наработки на отказ:
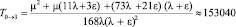часов.
Среднее время восстановления системы:
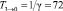часа.
Заключение
Таким образом, в рамках данной статьи рассмотрены предложенная автором обобщенная модель надежности системы, состоящей из n идентичных восстанавливаемых элементов, переходящей в состояние аварийного отключения при отказе s элементов и требующей проведения ремонта до исходного исправного состояния. Также рассмотрен частный случай модели и пример расчета показателей надежности.
Полученные теоретические результаты использовались в многолетней практике проектирования и эксплуатации систем хранения, обработки и передачи данных НИУ МЭИ (ТУ), Балаковской АЭС, ОАО «Красный Пролетарий» и ряда других предприятий.