Если неоднородная грунтовая среда в общем случае обладает свойством линейной ползучести, то зависимость между коэффициентом пористости и суммой главных напряжений имеет вид
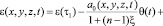
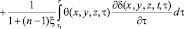, (1)
где
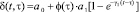; (2)
ε(t), θ(t) – эти функции также изменяются по координатам x, y, z; φ(t) – функция старения; a1, γ1 – параметры ползучести; τ1 – момент приложения внешней нагрузки; x – коэффициент бокового давления; а0 – коэффициент сжимаемости грунта, который в общем виде может зависеть от глубины исследуемой точки и времени; п – размерность рассматриваемой задачи.
Зависимость (1) при n = 1 и (2) для одномерной задачи теории уплотнения однородных грунтов впервые была применена В.А. Флориным [6]. Он теорию упругоползучего тела Г.Н. Маслова-Н.Х. Арутюняна [2] смог применить к описанию процесса уплотнения глинистых грунтов, обладающих свойством ползучести. Экспериментальные исследования С.Р. Месчяна [5] доказали применимость этой теории к водонасыщенным глинистым грунтам.
Функция старения φ(t), в (2), обычно представляется в виде [6, 2].
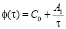. (3)
Здесь С0, А1 – опытные данные, t – время приложения нагрузки. Заметим, что кроме выражения (3) встречаются и другие меры ползучести, предложенные другими исследователями при изучении процесса, происходящего в бетоне. Эти зависимости, т.е. (1)–(3) будут описывать состояние скелета слабых глинистых грунтов, находящихся под давлением тех или иных внешних нагрузок. Для неоднородного упругого грунта зависимость (1) имеет вид
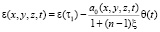. (4)
Выражение (4) для одномерной задачи теории консолидации однородного изотропного грунта имеет вид [7]
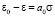, (5)
где величины ε0, a0 находятся путем эксперимента или вычислением; a0 – коэффициент сжимаемости; ε0 и e – коэффициенты пористости для начального и конечного моментов времени.
Основные разрешающие уравнения механики уплотняемых неоднородных упругоползучих грунтов определим следующим образом. Для этого возьмем уравнение уплотнения для пространственной задачи механики уплотняемых неоднородных грунтов без учета его ползучести, обладающих различными свойствами в вертикальном и горизонтальном направлениях:
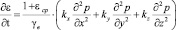. (6)
Если в место ε(t) примем (1), то уравнение (6) приводится к виду
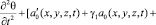
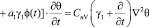. (7)
Начальные условия для уравнения (7) будут
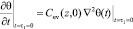, (8)
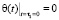. (9)
где
,
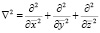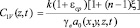; (10)
; 
; 
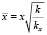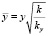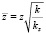. (11)
Следовательно, для нахождения искомой функции θ(t), кроме граничных условий, должны быть заданы еще два начальных условий. Одно из них определяется из (8), другое из (9).
Если состояние скелета глинистых грунтов подчиняется закону (5), то уплотняющая среда является упругой и уравнение (7) приводится к виду
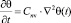. (12)
Начальное условие уравнения (12) имеет вид
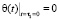. (13)
Следует заметить, что все основные уравнения механики уплотняемых водонасыщенных глинистых грунтов приведены относительно суммы главных напряжений θ(t). Можно эти уравнения представить относительно порового давления p(t). Для этого используем условие равновесия вида [6]
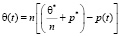. (14)
Тогда
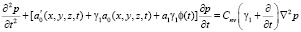. (15)
Начальными условиями для (15) будут
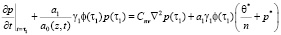, (16)
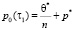. (17)
Для упругой задачи уравнение (12) имеет вид
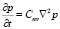, (18)
где θ*, p* – сумма главных напряжений и давление в поровой жидкости, соответствующие состоянию мгновенного уплотнения грунта.
Таким образом, решив уравнения (15),(18) при соответствующих краевых условиях находим решение той или иной задачи теории консолидации земляных масс. Если модуль деформации уплотняемого грунта по глубине не меняется, то основное уравнения уплотнения (15) в безразмерных координатах имеет следующий вид
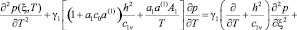
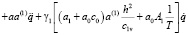, (19)
где
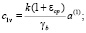
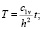
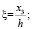
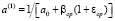. (20)
Начальными условиями для данной задачи будут:
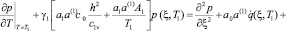
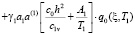; (21)
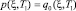, (22)
где
q0 (ξ,T1) = q (ξ,T1) – pстр.,
т.е. часть нагрузки, равная величине структурной прочности сжатия рстр, сразу же воспринимается скелетом грунта [1]. Если грунт деформируется только в вертикальном направлении, то по теории фильтрационной консолидации сумма избыточного порового давления и эффективного напряжения в грунте σ(z, t) в любой момент времени равна внешней нагрузке, т.е.
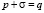. (23)
Для выяснения общего характера протекания процесса такого уплотнения достаточно будет рассмотреть отдельные решения одномерной задачи теории консолидации, физическая сторона которой не очень отличается от аналогичных решений трехмерных задач. С другой стороны, исследования одномерного уплотнения более доступны, чем двух и трехмерных. Кроме того, это дает возможность при рассмотрении процесса уплотнения учесть некоторые факторы, сильно влияющие на него, в частности, можно указать на одновременный учет старения и ползучести уплотняемых грунтов. В связи с этим ниже исследуем уравнение уплотнения (19), при условиях (21), (22). Для этого в момент времени t = τ1 рассмотрим уплотнение трехфазного наследственно – стареющего слоя грунта мощностью h, подверженного действию внешней распределенной нагрузки с интенсивностью q = q(z, t). Верхняя поверхность уплотняемого массива водопроницаема, а нижняя водонепроницаемая.
Граничные условия при ламинарном законе Дарси имеют вид:
; 
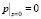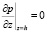. (24)
Второе граничное условие относится к глубине h, ниже которой фильтрации не происходит, так как на этой глубине градиент напора от действующей нагрузки q меньше начального градиента напора I0. Очевидно, что
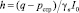. (25)
Следовательно, при модифицированном законе Дарси граничные условия (24) примут вид
; 
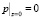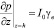. (26)
Таким образом, данную задачу можно сформулировать следующим образом. В безразмерных координатах требуется определить давление в поровой жидкости p(ξ, T), напряжение в скелете σ(ξ, T) и вертикальные перемещения верхней поверхности S(T) (осадок) грунтового слоя в области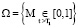 
, если P(ξ, T) удовлетворяет дифференциальному уравнению (19) начальным (21), (22) и граничным (26) условиям при (25).
Решение уравнения (19), удовлетворяющее указанным условиям, представим в виде
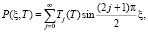
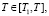
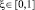. (27)
Здесь
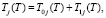(28)
T0j(T) – общее решение однородного уравнения (19), т.е. без правой части, когда Qj = 0, T1j(T) – частное решение неоднородного уравнения (19). При этом выражение T0j(T) имеет вид:
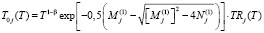, (29)
где
,
.
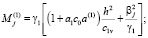
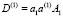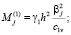
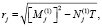
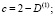
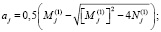
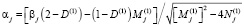Выражение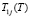 
соответственно имеет вид:
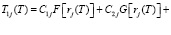
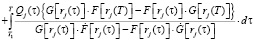. (30)
Здесь F(αj, c, rj) и G(αj, c, rj) соответственно являются вырожденными гипергеометрическими функциями первого и второго родов. При этом F(αj, c, rj) называется функцией Куммера. Она разлагается в степенной ряд
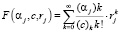. (31)
Тогда функция G(αj, c, rj) через F(αj, c, rj) выражается следующим образом:
.
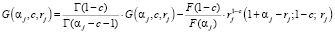Причем ряд (52) сходится при всех rj.
Таким образом, давление в поровой жидкости определяется по формуле (27) при (28)- (31). Напряжение в скелете грунта σ(ξ, T) – находится из выражения (23) т.е.
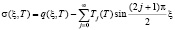. (32)
Для вычисления осадок S(T) грунта в безразмерной координате используем формулу вида
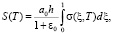(33)
где σ(ξ, T) – напряжение в скелете грунта.
Подставив выражение (32) в (33), находим
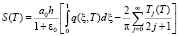. (34)
При Т → 0 имеем, что σ(ξ, T) → 0, а при Т → ∞ напряжение стремится к q.
Следовательно, если поровое давление изменится от q до 0, то напряжение принимает значение от 0 до q. При этом S(T) изменится от 0 до
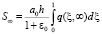. (35)
Если q(ξ, T) = q = const то из (47) находим, что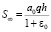 
, т.е. неустановившаяся осадка слоя уплотняемого грунта во времени изменяется в диапазонах от 0 до 
.
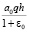Теперь рассмотрим решение задачи (15)–(17) в трехмерной постановке, применительно к уплотнению слоя упругоползучего грунта с учетом его свойства старения. Для этого рассмотрим грунтовой массив в виде параллелепипеда с водоупором на глубине h и с водонепроницаемыми стенками на 21 и 22, находящегося под действием равномерно распределенной нагрузки с интенсивностью q, приложенной на части поверхности этого параллелепипеда со сторонами 2a и 2b.
Применительно к данной расчетной схеме исследуемую задачу сформулируем так: требуется найти непрерывную функцию, отражающую изменение давлений в поровой жидкости и удовлетворяющую в области G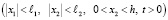
дифференциальному уравнению вида:
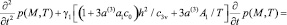
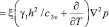(36)
начальным
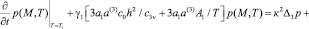
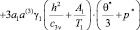(37)
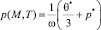, (38)
и граничным
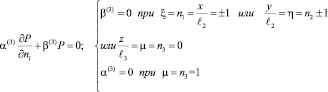(39)
условиям, соответствующим для исследуемой задачи. Здесь все величины записаны относительно безразмерных координат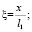 
,
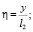
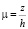где
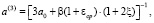
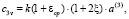
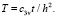(40)
с0, А1 – коэффициенты стареющего грунта; a1, γ1 – параметры ползучести. Кроме условий (37)–(39) в силу симметрии, функция P(ξ, η, μ) должна быть четной относительно x и h в отдельности.
Выражение (38) является начальным распределением порового давления исследуемого на уплотнение грунтового параллелепипеда. Если учесть, что для сильно сжимаемых водонасыщенных глинистых грунтов в начальный момент времени часть нагрузки, мгновенно приложенной нагрузки q к грунту, равная по величине структурной прочности сжатия рстр, сразу же воспринимается скелетом грунта [2], т.е.
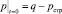, (41)
то это решение, т.е. начальное распределение порового давления в слое исследуемого массива для трехфазной земляной массы относительно безразмерных координат имеет вид:
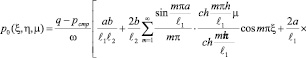
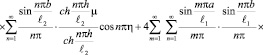
. (42)
Выражение (42) является решением следующего уравнения:
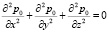, (43)
где x = ξl1; y = ηl2; z = μh. Решение уравнения (8) удовлетворяет граничным условиям вида:
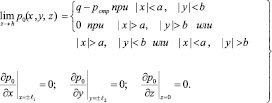(44)
Кроме них в силу симметрии функция p0(x, y, z) должна быть четной относительно х и у в отдельности, т.е.
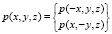(45)
Тогда решение уравнения (36), удовлетворяющее граничным условиям (39), получим в виде:
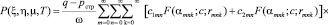
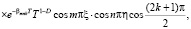(46)
где
:
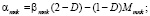
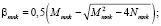
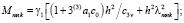
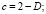
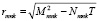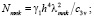
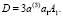
Здесь постоянные величины c1mnk и c2mnk находятся из начальных условий (37) и (38) при (40), (46). Следовательно, имеем:
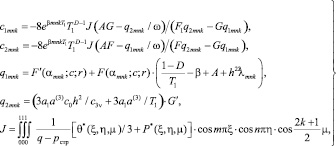, (47)
где F(αj, c, rj) и G(αj, c, rj) соответственно являются вырожденными гипергеометрическими функциями первого и второго родов.
Таким образом, по формуле (46) при величинах (47) можно вычислять значения давлении в поровой жидкости в уплотняемом наследственно-стареющим грунтовом параллелепипеде.
После определения давления в поровой жидкости сумму главных напряжений в скелете грунта можно вычислить по формуле:
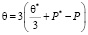(48)
где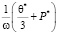 
и Р находятся из выражений (42) и (46).
Для определения осадки границ уплотняемого слоя будем пользоваться известной формулой, которая для принятой в данной задаче системы координат должна быть написана в виде:
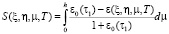. (49)
Для данной задачи выражение (49) можно представить так:
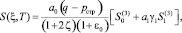(50)
где
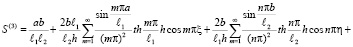
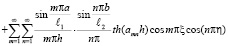, (51)
,
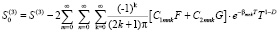
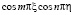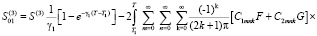
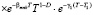
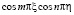dT. (52)
Таким образом, пространственная задача консолидации многофазного грунта с учетом его линейной ползучести и старения скелета, можно сказать решена полностью. Выражения (46), (48), (50), при (47), (51) (52) дают возможность установить закон изменения порового давления, сумму главных напряжений в скелете грунта и осадку уплотняемого массива во времени и пространственных координатах. Причем в эти решения, полученные в замкнутом виде, входят различные параметры грунта.
На основе полученных численных результатов могут быть построены кривые изменения порового давления, напряжения в скелете грунта, а также вертикальные перемещения верхней поверхности уплотняемого массива для данного момента времени и пространственных координатах. Причем значения давлений р в поровой жидкости и осадок слоя грунта в зависимости от толщины уплотняемого массива h существенно меняются.
Причем с увеличением мощности уплотняемого грунтового массива максимальное значение порового давления и время его наступления увеличивается. При этом значение осадки уменьшается в течение всего периода уплотнения. Так, например, при толщине слоя 5 м и 20 м максимальное значение порового давления отличается более чем 1,5 раза. Это означает, что с увеличением толщины уплотняемого слоя грунта уменьшается скорость нарастания напряжений в скелете грунта, а в уплотняемых грунтовых массивах с малыми мощностями скорость нарастания напряжений в скелете грунта не, только велика, что приводит к отставанию роста деформаций от роста напряжений в скелете грунта. В то же время при большой толщине уплотняемого слоя грунта скорость нарастания напряжений в скелете грунта будет небольшой и деформации уплотнения вследствие ползучести и старения скелета грунта протекает без заметного отставания.
Таким образом, максимальное значение порового давления в основаниях сооружений зависит от длины пути фильтрации, т.е. от размеров уплотняемого слоя грунта. Причем чем больше мощность уплотняемого грунтового массива, тем медленнее протекает фильтрационные процессы. Это означает, что процесс возрастания порового давления будет продолжаться за счет ползучести и старения скелета грунта.
Здесь следует отметить, что фундаментальное решение задачи консолидации грунтов с одновременным учетом ползучести и старения впервые исследовано в [8], а также в работах [3–4].