Выбор метода расчета и анализа электромагнитных параметров индукционной системы зависит от многих факторов среди которых вид электромагнитной системы, постановка задачи исследования, имеющиеся технически средства и программное обеспечение, квалификация исследователя.
Для расчета параметров индукционной нагревательной системы (ИНС) используется метод магнитных схем замещения, который на сегодняшний день является основным методом при проектировании индукционных нагревательных систем. В основе метода лежит принцип разбиения на участки пространства, по которому проходит магнитный поток, с дальнейшим определением их магнитных сопротивлений аналитическим или любым другим способом. После чего задача решается графическим или графоаналитическим методами, которые применяются при расчете магнитных цепей электромеханических устройств.
Алгоритм определения параметров ИНС локального и попутного воздействия будет отличатся количеством участков нагрева, на которые будет необходимо разделить систему [3].
Согласно выбранному методу разработаны магнитные и электрические схемы замещения для участков индукционной нагревательной системы. Ниже приведены схемы замещения и расчет параметров для элемента трубопровода типа «Фланец».
Методика расчета параметров «индуктор-нагрузка» для участка «Фланец»
Вариант расположения индуктора на участке «Фланец» представлен на рис. 1, а.
Допустим, что магнитное поле однородно по всей протяженности фланца, расположенного внутри индуктора (рис. 1, б). Это позволяет найти магнитное сопротивление Zф = ZфI + ZфI + ZфI и соответствующее ему сопротивление загрузки. Учитывая, что Zф известно, магнитную схему замещения можно рассматривать как четырехполюсник с П-образной схемой замещения, в котором Zф преобразуется во входное магнитное сопротивление индуктора (рис. 2).
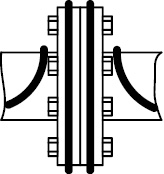
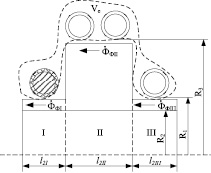
а) б)
Рис. 1. Картина магнитного поля индуктора и разделение потоков в системе
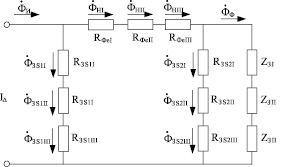
Рис. 2. Магнитная схема замещения индуктора
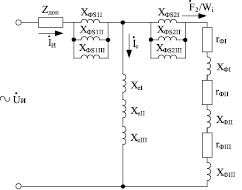
Рис. 3. Электрическая схема замещения индуктора
Согласно схеме замещения поток индуктора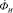 
, создаваемый обмоткой, разделяется на поток 
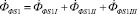, и поток 
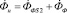, проходящий по нагреваемому телу 
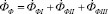и по прилегающей к нему части зазора 
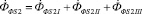и затем замыкающийся через область Ve (рис. 1, б) с магнитным сопротивлением RФе. Магнитные потоки 
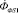и 
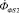проходят по участкам с магнитными сопротивлениям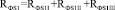и 
и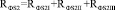 
.
Рассматриваемому участку индуктора ИНС соответствует дуальная электрическая схема (рис. 3). Сопротивление нагреваемого участка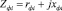 
зазор Хфs1, Хфs2 и пути обратного замыкания Xe приведены к числу витков индуктора Wi на каждом из участков и связаны с магнитными сопротивлениями этих участков соотношением
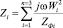. (1)
Дополнительное сопротивление Zдоп учитывает активное сопротивление обмотки индуктора r1 и сопротивление элементов, которые могут быть включены в цепь на участке до источника питания с известным напряжением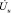 
и не связанно с магнитной схемой замещения. Внутреннее реактивное сопротивление индуктора x1м вычисляется как часть сопротивления зазора, используя вместо реального радиуса эквивалентный R1э, который определяется как [5]
;
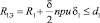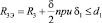, (2)
где d1 – толщина индуктора.
При условии Хфs2 = Хфs и Хфs1 = 0 сопротивление индуктора определяется как
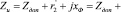
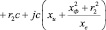, (3)
где xe = xФ + xc – реактивное сопротивление зазора и загрузки;
xe – сопротивление обратного замыкания;
с – коэффициент приведения параметров загрузки к индуктору [5]:
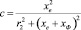. (4)
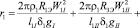
Активное сопротивление r1 вычисляется при условии равномерного распределения тока по одной стороне токопровода обмотки 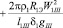[5]:
. (5)
где g – коэффициент заполнения обмотки медью по длине.
Сопротивление xs вычисляется как сумма сопротивлений на каждом отрезке
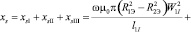
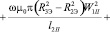
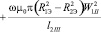. (6)
Для внешних индукторов картина магнитного поля, с внесением нагреваемого объекта, изменяется незначительно, а потому параметр xe можно определить по картине магнитного поля пустого индуктора
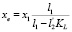, (7)
где KL – поправочный коэффициент индуктивности [5].
При этом x1 определяется как
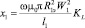. (8)
Для определения KL с погрешностью 3 % преобразуется формула для цилиндрических индукторов с тонкой обмоткой [5]
, 
,
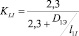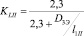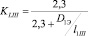, (9)
где D1Э = 2R1Э, D3Э = 2R3Э – эквивалентные диаметры.
Зависимость KL от D1Э/l1I и D3Э/l1II представлена кривой 5 на диаграмме рис. 2 [5].
Последовательность определения параметров индуктора справедлива для любого из элементов трубопровода и реализованы магнитные и электрические схемы для других участков трубопровода.
Расчет индуктивности контура
Для простоты решения поставленной задачи индуктивность витка будет находится суммированием индуктивностей, найденных для каждого участка трубопровода в отдельности. При этом рассматриваются два варианта расположения индуктора на поверхности объекта нагрева: расположение навитием и расположение витком с прямым и обратным проводником (рис. 4).
Расчет индуктивности прямолинейного участка с прямым и обратным проводником. Согласно [2] индуктивность прямолинейного провода при средней частоте
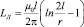, (10)
где l – длина провода,
r – радиус сечения провода.
Тогда взаимная индуктивность двух прямолинейных параллельных проводов располагающихся вдоль одной трубы находится как
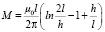, (11)
где h – расстояние между проводами.
Индуктивность системы проводов вдоль прямолинейного участка
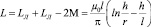, (12)
Индуктивность системы проводов вдоль прямолинейного участка на погонный метр [Гн/м]
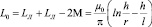, (13)
Расчет индуктивности прямолинейного участка с навитым индуктором (рис. 4, б). Взаимная индуктивность коаксиальных круговых контуров определяется как
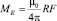, (14)
где R – радиус контуров (диаметр трубы),
F – величина зависящая от X [2]
Х – расстояние между витками.
Индуктивность кольца
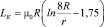, (15)
Следовательно, индуктивность спирали
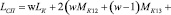
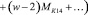, (16)
где w – количество витков спирали,
MК12 – взаимная индуктивность между 1-й и 2-й спиралью.
Учитывая резкое уменьшение F для 2R > X можно сделать допущение
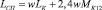, (17)
Взаимную индуктивность между прямой линией и спиралью можно приравнять ко взаимной индуктивности двух прямолинейных проводов, проходящих через центр трубы и по окружности трубы
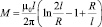. (18)
Тогда индуктивность контура спиралевидной намотки с одной стороны и длинной линии с другой
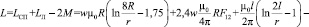
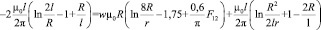. (19)
Для определения значения индуктивности на погонный метр уравнение (19) примет вид [Гн/м]
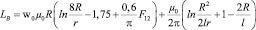, (20)
где w0 – количество витков на погонный метр.
Индуктивность более сложных участков находится разбиением их на простые, и дальнейшим суммированием индуктивностей простых участков.
а) б)
Рис. 4. Линейный участок промысловой трубы: а) индуктор расположен витком с прямым и обратным проводником, б) индуктор расположен навитием
Результирующее значение индуктивности контура сложной геометрии находится алгебраической суммой индуктивностей элементов обогреваемого трубопровода
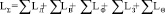. (21)
Расчет тока, потребляемого индуктором
Математически процесс индукционного нагрева можно описать законом Фарадея и законом Джоуля-Ленца [1]. В интегральной форме записываются как Закон Фарадея
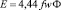, (22)
где Е – электродвижущая сила;
Ф – магнитный поток;
f – частота тока индуктора;
w – число витков индуктора.
Закон Джоуля-Ленца
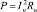, (23)
где P – мощность тепловая;
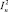– ток в нагреваемом объекте;
Rн – сопротивление объекта нагрева.
Выражение (23) описывает выделившеюся тепловую мощность в нагреваемом объекте. С другой стороны, полезную тепловую мощность, выделившуюся в объеме нагреваемого трубопровода, можно записать как [5]
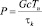, (24)
где G – масса объекта;
c – теплоемкость;
Тн – температура объекта;
τk – время нагрев.
Приравняем правые части уравнений (23) и (24)
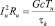, (25)
Отсюда сопротивление Rн будет
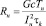, (26)
Ток в нагреваемом объекте Iн также можно выразить как
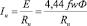, (27)
Подставив в выражение (27) выражение (26) получим
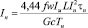, (28)
Выражение (28) после преобразования примет вид
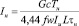, (29)
Используя выражение (29) можно определить ток в нагреваемой заготовке в зависимости от физических параметров объекта и его веса.
За счет эффекта вытеснения тока, который с повышением частоты значительно проявляется, ток в индукторе следует рассчитывать с учетом глубины проникновения магнитного поля в металл нагреваемого объекта. Для наглядности на рисунке 5 приведена схема распределения температуры при индукционном среднечастотном нагреве.
Мощность необходимая для нагрева объекта записывается как
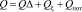, (30)
где QΔ – мощность, образованная вихревыми токами;
Qξ – мощность теплопроводности;
Qпот – мощность тепловых потерь;
QΔ + Qξ – представляет собой полезную мощность.
Рис. 5. Схема распределения тепла для расчета тока индуктора
Мощность QΔ (23) можно представить через удельное сопротивление ρ и толщиной слоя Δ, в котором протекают вихревые токи
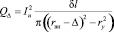, (31)
где rвн – внешний радиус объекта нагрева;
rу – условный радиус объекта нагрева;
ρ – удельное сопротивление
l – длинна объекта нагрева
Δ – глубина проникновения тока в объект нагрева.
Выражение для определения Qξ записывается как
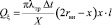, (32)
где λтр – коэффициент теплопередачи трубы;
Δt – температурный градиент;
Х – толщина участка трубы с теплопроводностью.
Мощность тепловых потерь имеет математическую форму записи
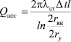, (33)
Необходимую мощность теплового потока, создаваемую индукционной нагревательной системой для нагрева жидкости,
Мощность теплового потока для нагрева жидкости определяется согласно [4] и определяет мощность которую необходимо создать индукционной нагревательной системой.
Тогда с учетом уравнений (30), (31), (32), (33) и произведя преобразования получим формулу для нахождения тока, потребляемого индуктором в зависимости от частоты, индукции и геометрии объекта определяется как
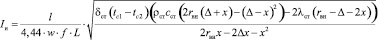, (34)
где δст – удельное электрическое сопротивление стали;
ρст – плотность стали;
сст – теплоемкость стали.
В выражении (34) известны все параметры за исключением числа витков w и индуктивности контура L, расчет которых приведен выше.
Выводы
Разработаны электрическая и магнитная схемы замещения индуктора ИНС участков нагреваемого нефтепровода для определения параметров индуктора.
Разработаны методики расчета индуктивности токопроводящего проводника учитывающие геометрические особенности нагреваемого объекта.
Получена зависимость для определения тока в индукторе учитывающая индуктивность индуктора, число витков и физические особенности объекта нагрева.