В современном мире информационные технологии являются неотъемлемой частью жизни человека и бизнес-процессов предприятий. Ежедневно огромные объемы информации создаются, передаются, обрабатываются и сохраняются с применением специализированных программно-аппаратных систем. Помимо потребительских технических характеристик систем, таких как: производительность, время задержки, емкость, размер, потребляемая мощность, не менее важными являются характеристики надежности, от которых зависит безопасность функционирования систем, сохранность данных, своевременность передачи и обработки информации, достоверность результатов.
Для оценки показателей надежности восстанавливаемых отказоустойчивых систем, состоящих из множества идентичных и независимых элементов, применяют модели надежности на базе восстанавливаемого элемента с двумя состояниями [1, 2]. Однако, такие модели не учитывают специфику некоторых видов технических элементов, в частности, узлов обработки информации, которые даже будучи в исправном состоянии требуют время для загрузки или реконфигурации программного обеспечения для того, чтобы начать обрабатывать информацию, и до завершения загрузки или реконфигурации пребывают в промежуточном пассивном состоянии. Переход в активное состояние обычно происходит за достаточно короткое, но все же конечное время. Кроме того, в пассивном состоянии элементы также могут отказывать, и интенсивность отказов в пассивном состоянии не равна нулю и не совпадает с интенсивностью отказов в активном состоянии. В такой ситуации возникает необходимость в рассмотрении моделей надежности специального элемента с тремя состояниями (активный, пассивный и неисправный) и систем на базе таких элементов.
В рамках научных исследований автора в области надежности систем хранения, передачи и обработки информации [3–10] возникла научная задача построения модели надежности мажоритарной вычислительной системы с учетом конечного времени активации вычислительных узлов, и различных интенсивностей отказов в активном и пассивном состояниях. Автором была построена модель надежности и выведены расчетные формулы показателей надежности для элемента с тремя состояниями. Далее модель и формулы были обобщены для системы из множества идентичных и независимых элементов с тремя состояниями с заданным нижним порогом для числа активных элементов, при котором система считается работоспособной. Наконец, обобщенная модель и формулы были применены для частного случая мажоритарной вычислительной системы.
Модель надежности элемента с тремя состояниями. Рассмотрим элемент со следующим множеством состояний и условий переходов между ними:
● Состояние P – элемент исправен, но пассивен: не выполняет требуемые функции в силу выполнения инициализации программного обеспечения (активации). Из этого состояния элемент с интенсивностью γN (активация) может перейти в состояние A, либо с интенсивностью λР (отказ в пассивном состоянии) перейти в состояние F.
● Состояние A – элемент исправен и активен (выполняет требуемые функции). Из этого состояния элемент с интенсивностью λA (отказ в активном состоянии) может перейти в состояние F.
● Состояние F – элемент неисправен. Из этого состояния элемент с интенсивностью μN (ремонт) может перейти в состояние P.
Тогда, с учетом вышесказанного имеем следующий граф состояний (рис. 1):
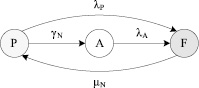
Рис. 1. Марковская модель надежности элемента с тремя состояниями
Математическая модель (система уравнений Колмогорова-Чепмена):
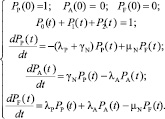(1)
где λА – интенсивность отказов элемента в активном состоянии, λР – интенсивность отказов в пассивном состоянии, μN – интенсивность ремонта, и γN – интенсивность активации (перехода из пассивного состояния в активное состояние).
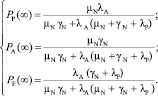
Мы ограничимся выводом аналитического решения для стационарного случая при t → ∞, когда марковский процесс становится установившимся, и производные вероятностей по времени стремятся к нулю. Тогда мы имеем дело с системой алгебраических уравнений, и, решая ее, получаем формулы для стационарных вероятностей всех состояний:
(2)
Соответственно, стационарный коэффициент готовности элемента, с учетом того, что только в состоянии A элемент активен и выполняет требуемые функции:
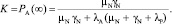(3)
Примечание. При γN → ∞, коэффициент готовности K → μN/(μN + λА).
Среднее время наработки на отказ нетрудно определить, используя топологический метод для моделей надежности на базе цепей Маркова. Оно определяется как отношение суммы вероятностей работоспособных состояний к взвешенной сумме вероятностей работоспособных состояний, умноженных на соответствующие суммы интенсивностей переходов из работоспособного состояния во все неработоспособные:
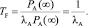(4)
Наконец, среднее время восстановления, включающего в себя ремонт и активацию, нетрудно определить из взаимосвязи коэффициента готовности со средними временами наработки на отказ и восстановления:
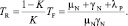(5)
Модель надежности системы идентичных и независимых элементов. Рассмотрим систему n независимых и идентичных элементов с тремя состояниями. Каждый элемент может независимо находится в одном из трех состояний.
В силу идентичности элементов пусть каждое состояние системы отражает определенное количество i активных элементов, j неисправных элементов, 0 ≤ i ≤ n, 0 ≤ j ≤ n, i + j ≤ n, и n – i – j пассивных элементов. Общее количество состояний системы (n + 1)(n + 2)/2. Из состояния (i, j) система может перейти:
● С интенсивностью iλА в состоянии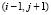 
: отказ одного из активных элементов.
● С интенсивностью (n – i – j)γN в состояние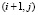 
: активация одного из пассивных.
● С интенсивностью (n – i – j)λP в состояние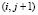 
: отказ одного из пассивных.
● С интенсивностью jμN в состояние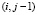 
: ремонт одного из неисправных.
Кроме того, пусть система считается работоспособной тогда, когда не менее s элементов активны, 1 ≤ s ≤ n. Соответственно, состояния (i ≥ s, j) системы считаются работоспособными, а состояния (i < s, j) неработоспособными.
Тогда, с учетом всего вышесказанного имеем следующий граф состояний системы независимых и идентичных элементов с тремя состояниями (рис. 2).
Следует отметить, что в силу независимости элементов для определения вероятностей всех состояний системы нет необходимости в трудоемком составлении и решении системы уравнений Колмогорова-Чепмена. Стационарная вероятность каждого состояния (i, j) равна произведению вероятности одновременного нахождения i элементов в активном состоянии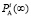 
, вероятности одновременного нахождения j элементов в неисправном состоянии 
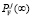, вероятности одновременного нахождения n – i – j элементов в пассивном состоянии 
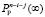, умноженного на число всевозможных сочетаний 
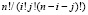активных, неисправных и пассивных элементов:
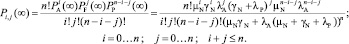(6)
Для расчета показателей надежности системы нам также понадобится сумма вероятностей всех состояний системы при заданном количестве i активных элементов:
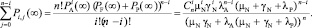(7)
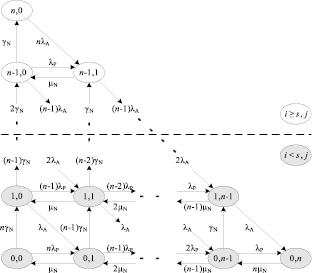
Рис. 2. Модель надежности системы n идентичных и независимых элементов с тремя состояниями и заданным нижним порогом s для числа активных элементов
Тогда при заданном нижнем пороге s для числа активных элементов, при котором система работоспособна, стационарный коэффициент готовности системы определяется как сумма вероятностей всех работоспособных состояний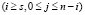 
:
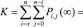
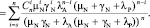(8)
Соответственно, среднее время наработки на отказ системы определяется как отношение суммы вероятностей всех работоспособных состояний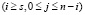 
к взвешенной сумме вероятностей граничных работоспособных состояний 
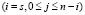, умноженных на соответствующие интенсивности iλА перехода в неработоспособные состояния. Заметим, что для всех граничных работоспособных состояний интенсивность перехода в неработоспособные состояния одинакова и равна sλА:
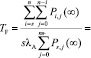
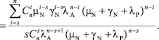(9)
Наконец, среднее время восстановления, нетрудно определить из взаимосвязи коэффициента готовности со средними временами наработки на отказ и восстановления:
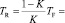
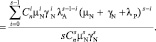(10)
Модель надежности мажоритарной вычислительной системы с тремя узлами. Отказоустойчивая вычислительная система с тремя узлами и мажоритарным выбором результата вычислений может рассматриваться как частный случай вышеописанной системы при n = 3 и s = 2. Вычислительная система дает достоверный результат в случае, если не менее двух из трех узлов исправны и активны (выполняют вычисления). Тогда имеем следующий граф состояний рассматриваемой вычислительной системы (рис. 3).
Формула для расчета коэффициент готовности вычислительной системы выводится путем подстановки n = 3 и s = 2 в формулу 8:
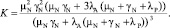(11)
Аналогично выводим формулу для расчета среднего времени наработки на отказ:
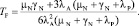(12)
Наконец, формула для расчета среднего времени восстановления:
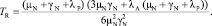(13)
Рис. 3. Модель надежности мажоритарной вычислительной системы с тремя узлами
Пример расчета показателей надежности. Пусть задана мажоритарная вычислительная система с тремя узлами. Интенсивность отказов узлов в активном состоянии λА = 1/2920 час-1 (в среднем три раза в год), интенсивность отказов в пассивном состоянии λP = 1/8760 час-1 (в среднем раз в год), интенсивность активации γN = 20 час-1 (в среднем три минуты) и интенсивность ремонта μN = 1/24 час-1 (в среднем одни сутки).
Рассчитаем показатели надежности мажоритарной вычислительной системы:
● По формуле 11 получаем коэффициент готовности: KF ≈ 0,999801.
● По формуле 12 получаем среднее время наработки на отказ: TF ≈ 60547 часов.
● По формуле 13 получаем среднее время восстановления: TR ≈ 12,058 часов.
Заключение
Таким образом, в рамках данной статьи автором рассмотрена модель надежности мажоритарной вычислительной системы с учетом конечного времени активации узлов, и различных интенсивностей отказов в активном и пассивном состояниях. Автором разработана модель надежности и выведены расчетные формулы показателей надежности для элемента с тремя состояниями. Далее модель и формулы обобщены для системы из множества идентичных и независимых элементов с тремя состояниями с заданным нижним порогом для числа активных элементов, при котором система считается работоспособной.
Наконец, обобщенная модель и формулы применены для частного случая мажоритарной вычислительной системы с тремя узлами. Также приведен пример расчета стационарного коэффициента готовности, среднего времени наработки на отказ и среднего времени восстановления мажоритарной вычислительной системы.
Полученные теоретические результаты использовались в многолетней практике эксплуатации, развития и проектирования систем хранения и обработки данных НИУ МЭИ (ТУ), Балаковской АЭС, ОАО «Красный Пролетарий» и ряда других предприятий.