Введение
Электромагнитный способ трансформации кинетической и потенциальной энергии в энергию разрушения материалов, реализованный в электромагнитных механоактиваторах (ЭММА) [1,2,3], позволяет решить комплекс задач, стоящих перед производителями продукции при регламентированных технологией требованиях к гранулометрическому составу получаемых частиц [4,5], температурному режиму переработки материалов [6,7], а также требований к минимальной энергоемкости готовой продукции [8] и эфекту намола [9,10]. При этом наиболее актуальной является проблема энергосбережения на стадии тонкого и сверхтонкого диспергирования прочных материалов. На образование новых поверхностей затрачивается энергия, доля которой в значительной степени определяется условиями энергоподвода и соотношениями режимов работы ЭММА (скоростных и электромагнитных) [11], которые в свою очередь зависят от конструктивного исполнения устройства и устанавливаются в соответствии со значениями энергии начала разрушения частиц перерабатываемого материала [12]. Доля этой энергии увеличивается с ростом дисперсности твердой фазы, что предопределяет создание в рабочих объемах аппаратов более жестких силовых и энергетических условий измельчения по мере уменьшения размеров частиц. При этом сила воздействия на частицы продукта со стороны размольных элементов (элементов магнитоожиженного слоя) ЭММА возрастает с увеличением величины силы тока в обмотках управления до определенного экстремального значения. Определение диапазона регулирования силы тока в обмотках управления (ОУ) является одной из актуальных задач при проектировании энергоэффективных ЭММА.
Целью исследования является разработка методики расчета диапазона регулирования силы тока в ОУ ЭММА цилиндрических конструкций, предназначенных для диспергировании прочных материалов.
Материалы и методы исследований
Объектом исследования является исследование зависимостей рациональных электромагнитных режимов работы ЭММА цилиндрических конструкций от строения электромагнитного поля в объемах обработки продукта.
Результаты исследования и их обсуждение
При переработке прочных материалов в конструкциях ЭММА предусмотрена установка нескольких ОУ, расположенных как в корпусе устройства, так и на его внутреннем роторе (или на обеих частях магнитопровода одновременно) [13, 14]. За счет применения дополнительных обмоток управления повышается качество промагничивания ферромагнитной загрузки, что способствует усилению диспергирующих нагрузок по частицам перерабатываемого продукта. При цилиндрическом исполнении рабочего объема с расположением обмотки управления в корпусе устройства , магнитный поток Ф, создаваемый электрическим током, протекающим по обмотке ОУ, замыкается по участкам магнитопровода – корпусу I, рабочему объему II и внутреннему цилиндру (ротору III) (рис. 1). Площадь сечения корпуса значительно меньше площади сечения внутреннего цилиндра [15]. В корпусе магнитная индукция ВК имеет большее значение, чем в цилиндре. А так как толщина корпуса незначительна по сравнению с его внешним радиусом, то можно считать, что магнитный поток Ф распределен равномерно по его толщине.
На рис. 2 представлен график распределения напряженности магнитного поля Н0 внутри рабочего объема. Максимально допустимое значение индукции магнитного потока в корпусе ВК ДОП определяется путем интегрирования значений индукции в рабочем объеме у внутренней поверхности корпуса (при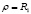 
, где 
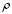– радиус точки объема обработки, R1 –внутренний радиус корпуса) по половине этой поверхности с последующим делением результата на минимально площадь сечения корпуса Sк.
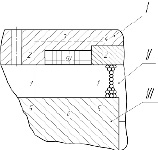
Рис. 1. Конструктивная схема магнитопровода ЭММА цилиндрического исполнения: I – корпус II – рабочий объем с феррошарами; III – внутренний цилиндр; I, 2,…,6 – участки магнитопровода; ОУ – обмотка управления
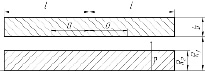
а б
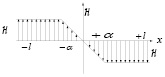
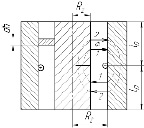
Рис. 2. Расчетные участки элементов ЭММА: а – геометрические параметры участков; б – схема распределения силовых линий магнитного поля в рабочем объеме ЭММА; 2l – высота рабочего объема; 2а – высота паза для размещения обмотки управления; в- толщина корпуса; R1и R2 – соответственно радиусы цилиндрических поверхностей корпуса и ротора; ρ- радиус произвольной точки рабочего объема.
На участке "l-α" поле в рабочем объеме ЭММА цилиндрических конструкций является равномерно-радиальным, причем его параметры (напряженность и индукция) увеличиваются по радиусу устройств к внутренней цилиндрической поверхности, составляющей рабочий объем, по линейному закону. Среднее значение напряженности определяется выражением: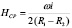 
. Параме тры магнитного поля в объеме обработки ЭММА цилиндрических конструкций увеличиваются по радиусу к внутренней поверхности, образующей рабочий объем, по линейному закону [16]: 
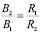и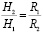 
.
Выражения для определения напряженности Н0 и индукции В0 магнитного поля в любой точке рабочего объема ЭММА цилиндрических конструкций имеют вид:
; 
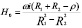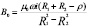, (1)
где ρ - радиус точки объема обработки при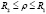 
.
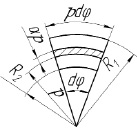
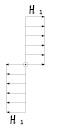
а б в
Рис. 3. Схема к расчету параметров электромагнитного поля на участках рабочего объема: а – продольный разрез устройства; б – элемент рабочего объема; в – схема распределения силовых линий магнитного поля на участках „l-α“
С учетом зависимостей (1) и параметров расчетной схемы, представленной на рисунке 3, выражение для определения магнитной энергии имеет вид:
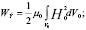
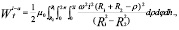
где V0 – объем обработки продукта.
После интегрирования и ряда несложных математических преобразований получим формулу для вычисления энергии в рабочем объеме ЭММА на участке „l-α“:
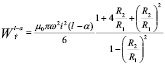(2)
Так как магнитная энергия определяется выражением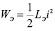 
(здесь LЭ –ин дуктивность ОУ), то можно записать равенство:
Отсюда получаем формулу для определения индуктивности обмотки управления на участке „l-α“:
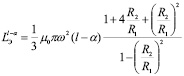(3)
Формулы (2) и (3) получены для идеализированного случая, когда обмотка управления с током, создающим магнитное поле в рабочем объеме аппарата, представлена в виде одного витка с нулевым диаметром провода. Между тем, при конструктивном исполнении обмотка управления занимает существенную часть длины ЭММА. Поэтому более точно ее можно представить в виде токового слоя, расположенного симметрично относительно середины рабочего объема на внутренней поверхности цилиндрического корпуса. При этом линейная плотность тока в слое σi определена выражением σi=WyIy/2α, (здесь Wy- число витков в ОУ; Iy - сила тока в ОУ).
На участках „α“ напряженность магнитного поля в рабочих объемах ЭММА меняется линейно (при фиксированном значении ρ) по закону:
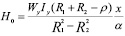. (4)
Магнитная энергия на этом участке равна:
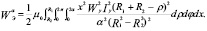
Или после интегрирования и математических преобразований может быть представлена в виде:
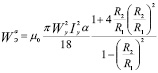. (5)
Суммарная магнитная энергия в рабочем объеме на участках„l-α“и „α“ определена по формуле:
,
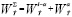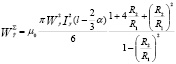. (6)
Индуктивность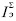 
обмотки управления ЭММА можно определить из равенства
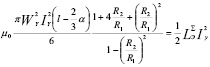
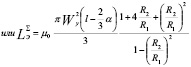(7)
На основании подученных данных магнитный поток Ф, проходящий по корпусу устройства, можно представить в виде:
.
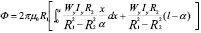Интегрирование этого выражения как интеграла, содержащего линейные множители, , дает окончательное искомое уравнение:
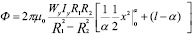
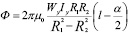(8)
Принимая во внимание, что корпус устройства является наиболее насыщенным в магнитном отношении участком магнитопровода, и, исходя из цилиндрического конструктивного исполнения этого участка, можно записать:
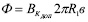. (9)
При совместном решении уравнений (8) и (9)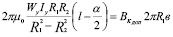 
получаем выражение для определения величины индукции в корпусе устройства:
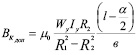. (10)
Анализ полученной зависимости показывает, что при проектировании ЭММА цилиндрических конструкций величину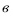 
следует выбирать наименьшей в корпусе, т.е. в месте расположения обмотки управления (участок III на рис. 1). Для обеспечения высоких регулировочных способностей аппарата корпус необходимо изготавливать из магнитного материала с высоким значением магнитной проницаемости и индуктивности насыщения. Определив по кривым намагничивания для выбранных материалов самого напряженного в магнитном отношении участка магнитопровода ВК ДОП, можно установить максимальное значение и диапазоны регулирования силы тока Iу в ОУ, обеспечивающие энергоэффективное проведение процесса механоактивации [17]:
;
,
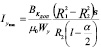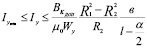где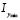 
- минимальное значение силы тока, при котором обеспечивается формирование структурных групп из ферромагнитных элементов в рабочем объеме ЭММА [1].
Заключение
Результаты исследований представляют методику расчета диапазонов регулирования силы тока в обмотках управления ЭММА цилиндрических конструкций, при которых достигается максимизация дисперсности перерабатываемого продукта при минимальных энергозатратах на формирование диспергирующих усилий в магнитоожиженном слое размольных ферротел.