Одна из наиболее острых проблем в информационных технологиях – это защита данных от искажений. Как каналы передачи данных, так и носители информации на сегодняшний день остаются далекими от совершенства, несмотря на все усилия производителей современных аппаратных средств. Кабельные и беспроводные линии передачи информации подвержены воздействию внешних помех, искажающих форму передаваемых сигналов и тем самым делающих невозможным однозначное распознавание информации на стороне приемника, магнитные и оптические носители информации чувствительны к физическим повреждениям, делающим невозможным чтение информации из отдельных участков на поверхности носителя.
В настоящее время в системах хранения и передачи данных применяют различные технологии информационного резервирования с применением специальных алгоритмов кодирования на базе корректирующих кодов, в частности, кодов Рида-Соломона [1], которые за счет использования избыточной информации делают возможным исправление искажений. Однако, введение избыточной информации снижает долю полезной информации в передаваемых сетевых кадрах, соответственно, возникает задача анализа вероятностей [2] искажения информации, и выбора между избыточностью и устойчивостью к искажениям.
В рамках научных исследований автора в области надежности систем хранения, передачи и обработки данных [3-10] возникла научная задача вероятностного анализа невосстанавливаемых искажений кадров при передаче по каналам связи, закодированных с применением кодов Рида-Соломона, и разработки алгоритма выбора оптимальной кратности исправляемых искажений. Соответственно, автором было проведен анализ вероятностей искажений, и имитационное моделирование кодирования, искажения и декодирования сетевых кадров. Также был предложен простой алгоритм выбора кратности исправляемых искажений при заданной вероятности искажения бита, размере кадра, длине поля полезной информации и допустимой вероятности невосстанавливаемого искажения кадра.
Кодирование информации с применением кодов Рида-Соломона. В современной практике при использовании кодов Рида-Соломона чаще всего применяется кодирование информации, представленных в виде блоков размером k байтов. Далее путем специального алгоритма кодирования, базирующегося на алгебраическом представлении информации в виде полиномов над полем Галуа GF(28) и их преобразования над этим полем вычисляются r контрольных байтов. При систематическом кодировании контрольные байты добавляются к информационным байтам, и в итоге получается кадр размером n байтов (рис. 1).
Рис. 1. Структура кадра с информационными и контрольными байтами
Количество контрольных байтов чаще всего выбирается четным числом, и оно равно удвоенной кратности t исправляемых искажений – максимальному количеству искаженных байтов, которые можно гарантированно восстановить, используя алгоритм декодирования.
Таким образом, n = k + r и r = 2t. При использовании кодов Рида-Соломона для байтовых блоков, максимальный размер кадра составляет 28 – 1 = 255 байтов в силу свойств поля Галуа GF(28). Кроме того, при фиксированной длине кадра при увеличении числа r контрольных байтов с целью увеличения кратности исправляемых искажений t и снижения вероятности невосстанавливаемого искажения кадра (когда при передаче кадра искажается более t байтов), на долю информационных байтов остается меньшее количество n – 2t.
Анализ вероятностей искажения информации. Информация может искажаться либо при передаче по каналам передачи данных, либо при хранении на каком-либо носителе информации (жесткий диск, оптический диск и т.п.).
Для каналов передачи данных, как правило, известна вероятность искажения бита. Данные передаются в виде последовательности битов, и каждый из них может подвергнуться искажению. Здесь мы сделаем несколько важных допущений (ради упрощения анализа):
● Вероятность искажения того или иного бита в том или ином байте в канале передачи данных одна и та же, и не зависит от позиции байта в кадре и бита внутри байта.
● Канал передачи данных не обладает «памятью», и вероятность искажения очередного передаваемого бита не зависит от того, были ли искажены предыдущие биты.
● Вероятность искажения бита не меняется со временем или меняется достаточно медленно, и в пределах отрезка времени, требуемого для передачи кадра, вероятность искажения бита можно считать постоянной.
При соблюдении вышеперечисленных условий, передачу кадра длины n можно считать последовательностью из n независимых испытаний по передаче отдельных байтов, в свою очередь, в рамках передачи отдельного байта мы имеем дело с последовательностью из 8 независимых элементарных испытаний по передаче отдельных битов. В итоге мы имеем дело с последовательностью из 8n элементарных независимых испытаний, которую мы можем также интерпретировать, как n независимых серий по 8 независимых элементарных испытаний в каждой серии. Особо отметим также, что в случае искажения нескольких битов, они могут различными способами располагаться внутри кадра, состоящего из n байтов, например, 8 искаженных битов могут «уместиться» внутри одного байта, а могут «распылиться» по 8 различным байтам – и это будут принципиально различные ситуации с точки зрения корректирующей способности кодов Рида-Соломона.
Чтобы оценивать вероятности искажения одного, нескольких или всех байтов в кадре на основе информации о базовой вероятности искажения одного бита мы должны обратиться к математическому аппарату теории вероятностей.
Пусть, p – заданная вероятность искажения бита. Тогда, вероятность того, что исказится байт, равна вероятности того, что хотя бы один бит в байте исказится:
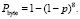(1)
Тогда, согласно биномиальному закону распределения числа искаженных байтов, получаем вероятность того, что исказится ровно h байтов в кадре, состоящего из n байтов, при заданной вероятности p искажения бита:
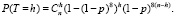(2)
Искаженные биты могут «попадать» в какие-то байты, а в какие-то «не попадать». Формула определяет вероятность искажения ровно h байтов, при условии целостности остальных n – h байтов, во всех подходящих вариантах искажения λ = h…8h битов, при условии целостности остальных 8n – λ битов в кадре и условии, что в каждый из h байтов «попадет» хотя бы один искаженный бит в каждом варианте, и также учитываются все сочетания искаженных h байтов по n байтам в кадре.
Теперь, имея формулу для вероятности искажения ровно h байтов в кадре длиной n при заданной вероятности искажения бита p, нетрудно вывести формулы для вероятности отсутствия искажения (T = 0), вероятности восстанавливаемого искажения (1 ≤ T ≤ t) и вероятности невосстанавливаемого искажения (T > t).
Тогда, формула для вероятности отсутствия искажения:
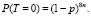(3)
Формула для вероятности восстанавливаемого искажения:
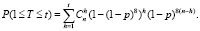(4)
Наконец, формула для вероятности невосстанавливаемого искажения:
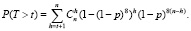(5)
Выбор кратности исправляемых искажений. При использовании кодов Рида-Соломона за возможность исправления t искаженных байтов приходится «платить» r = 2t контрольными байтами, и в условиях, когда у нас задана фиксированная длина кадра n, при увеличении кратности исправляемых искажений t на долю полезной информации остается все меньшее k = n – r число байтов. В пределе, коды Рида-Соломона могут обеспечить исправление вплоть до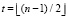 
байтов, при этом, если n нечетно, n – 1 байтов будут контрольными, так как 
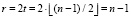, и всего один байт останется на долю полезной информации, так как k = n – (n –1) = 1.
Очевидно, что для выбора «разумной» кратности исправляемых искажений необходимо отталкиваться от каких-то критериев и ограничений.
Пусть заданы следующие исходные параметры для задачи выбора кратности:
n – фиксированная длина кадра в байтах.
p – базовая вероятность искажения бита.
kmin – требуемое минимальное число байтов полезной информации в кадре.
Pmax – допустимая вероятность невосстанавливаемого искажения кадра.
Далее, исходя из условия что, должно соблюдаться требование по допустимой вероятности невосстанавливаемого искажения кадра и требование на минимальное число байтов полезной информации, можно предложить следующую модель задачи выбора кратности исправляемых искажений:
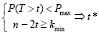(6)
Если, невозможно найти параметр t, удовлетворяющий обоим условиям, то, очевидно, применение кодов Рида-Соломона нецелесообразно. Кроме того, очевидно, если вероятность искажения вообще хотя бы одного байта меньше заданной допустимой границы, то есть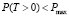 
, то применение кодов Рида-Соломона также нецелесообразно. Ниже приведена схема алгоритма для оценки целесообразности применения кодов Рида-Соломона и выбора кратности исправляемых искажений (рис. 2).
Пример выбора кратности исправляемых искажений. Задана длина кадра n = 36 байтов, минимальное число байтов полезной информации kmin = 32, вероятность искажения бита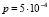 
и допустимая вероятность невосстанавливаемого искажения кадра Pmax = 0,001.
Рассчитаем сначала вероятность возникновения искажения хотя бы в одном байте кадра, и тем самым, оценим оправданность использования кодов Рида-Соломона:
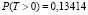
Очевидно, что эта вероятность значительно выше допустимой границы Pmax = 0,001, так что применение кодов Рида-Соломона вполне оправдано. Теперь попробуем выбрать кратность t исправляемых искажений, исходя из двух условий:
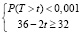
Очевидно, для заданного требуемого числа байтов полезной информации, можно рассматривать только два варианта t = 1 и t = 2. В этих вариантах вероятности невосстанавливаемого искажения кадра по формуле 5 равны: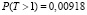 
и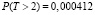 
. Очевидно, что вариант t = 2, удовлетворяет обоим условием.
Таким образом, применение кодов Рида-Соломона целесообразно, и выбранная кратность исправляемых искажений t = 2.
Заключение
Таким образом, в рамках данной статьи рассмотрен проведенный автором вероятностный анализ искажений при передаче кадров данных, закодированных с применением кодов Рида-Соломона.
Также рассмотрен предложенный автором алгоритм выбора кратности исправляемых искажений при заданной вероятности искажения бита, размере кадра, длине поля полезной информации и допустимой вероятности невосстанавливаемого искажения кадра.
Наконец, приведен пример выбора кратности исправляемых искажений.
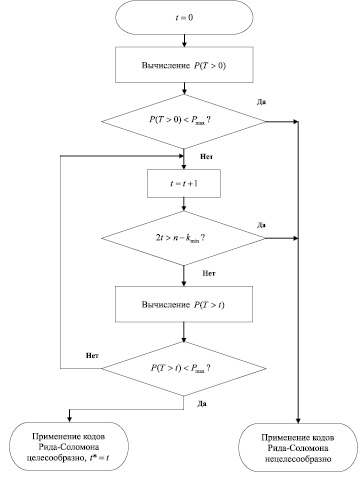
Рис. 2. Схема алгоритма для оценки целесообразности применения кодов Рида-Соломона и выбора кратности исправляемых искажений
Полученные теоретические результаты использовались в многолетней практике эксплуатации, развития и проектирования систем хранения и передачи данных НИУ МЭИ (ТУ), Балаковской АЭС, ОАО «Красный Пролетарий» и ряда других предприятий.