Для разработки прочных и мерзлых грунтов применяются различные типы землерезных машин: баровые, дисковые, роторные. К режущим органам вращательного действия относятся фрезы и буры; к режущим органам поступательного действия – рыхлители, бары [1]. Последние по принципу резания занимают промежуточное положение между первыми и вторыми.
Особенности разработки грунтов фрезерным рабочим органом не позволяют использовать напрямую выводы различных теорий резания грунтов.
Цель исследования
Работы, проведенные в области фрезерования грунтов принимают ряд неточных теоретических допущений. В связи с этим, необходима разработка методики уравнений движения фрезерных рабочих органов.
Существует три подхода к решению задач в механике грунтов и, в частности, в теории резания. Реологический, основанный на разработке моделей составляющих совокупность упругих, вязких и пластичных элементов: теоретический, базирующийся на использовании механики сплошной среды и экспериментальный.
Первый метод не позволяет получать адекватные результаты и в основном служит для анализа закономерностей изменения деформации и осадок оснований сооружений.
Второй метод дает качественную картину разрушения грунта, позволяет, что очень важно, дать весомость составляющих сил резания относительно друг друга, учитывать пространственную модель работы. Недостатком этого метода является низкая точность расчетов (расхождение до 100 %). Именно поэтому проектировщики при проектировании фундаментов основываются на опытных данных СНИПов, а конструкторы землеройных машин на экспериментальных результатах [1, 2, 3].
Третий метод, основанный на экспериментальных приближенных данных, дает достаточные для расчетов параметров нагружения и режима землеройных машин результаты, но не позволяет вводить в схемы новые нагрузки и определять отношение различных факторов нагружения.
Очевидно, что для достижения цели исследования, нет необходимости в создании новой теории резания грунтов. В связи с требованием введения дополнительных условий и особенностей фрезерования грунтов и получения качественной картины процесса корректно использовать второй метод установления сил сопротивления грунта разрушению.
Материалы и методы исследования
Для установления закономерностей, характеризующих силы сопротивления движению фрезерного рабочего органа в процессе разработки траншеи, необходимо составить и решить уравнения движения рабочего органа. Рассмотрен исследуемый рабочий орган как одномассовая система с двумя степенями свободы: вокруг оси вращения фрезы и в направлении подачи инструмента на забой [4].
Фрезерный рабочий орган предназначен для выполнения двух операций: проходки траншеи и уширения ее основания. В связи с последовательным протеканием по времени этих операций соответствующие им уравнения движения рассмотрены отдельно.
В случаях изучения режима работы фрезерного инструмента в среде глинистого раствора требуется учитывать влияние сопротивлений среды функционирования на параметры проходки, для этого в уравнениях движения введен дополнительный крутящий момент Мдоп., возникающий в результате действия гидродинамических и инерционных сопротивлений глинистого раствора. Значения Мдоп. вычисляются по известным зависимостям (1), которые для удобства дальнейших преобразований в уравнениях движения не представлены в развернутом виде.
С учетом направления сил моментов, действующих на инструмент, уравнения движения фрезерного рабочего органа в процессе разработки траншеи имеют вид (2, 3, 4)
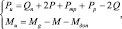 (1)
(1)
с учетом значений входящих в систему (1) величин
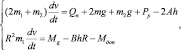 (2)
(2)
где Рu, Mu – соответственно сила инерции и момент инерционных сил; Qn, Mg – соответственно усилие подачи и крутящий момент привода фрезерного инструмента; Р, Ртр – соответственно вес одной фрезы с приводом и транспортера; Рр – реактивная сила действия транспортера; m1 – масса фрезы и жестко связанных с ней элементов; m2 – масса транспортера; ω – соответственно линейная скорость подачи и угловая скорость вращения рабочего органа; R – расстояние от оси вращения фрезы до центра приложения сил резания грунта; h – толщина срезаемой g – ускорение силы тяжести; Q, M, M – соответственно сопротивление усилию подачи и крутящие моменты, необходимые для преодоления сопротивлений грунта разрушению, влияния среды глинистого раствора и массы волочения [4].
Система уравнений (1) представляет собой математическую модель движения фрезерного рабочего органа, при исследовании которой принимались следующие допущения:
– усилия подачи, вес транспортера и реактивная сила действия транспортера представляют собой равномерно распределенную нагрузку и их действие на каждую из фрез одинаково;
– колебаниями сил сопротивления грунта разрушению за счет вариации силы резания и их изменением по глубине проходки пренебрегаем в связи с одновременностью работы нескольких резцов и ускорением за счет этого динамической составляющей силы резания;
– рабочий орган, штанга и транспортер представляют собой жесткую конструкцию; упругие колебания в этих элементах не учитываются;
– колебаниями в канатной или гидравлической системе механизма подачи фрезерного инструмента на забой можно пренебречь [5].
Исследуемый рабочий орган конструктивно выполнен в виде двух фрез, расположенных симметрично относительно оси инструмента. Нагружение фрез в процессе взаимодействия с грунтом одинаково, они движутся по идентичным траекториям и не отличаются друг от друга по конструкции. Эти обстоятельства позволяют при составлении и решении уравнений движения рабочего органа рассматривать одну фрезу, а полученные результаты обобщать на весь рабочий орган.
Процесс разработки траншеи фрезерным рабочим органом осуществляется в двух режимах работы инструмента: установившемся и неустановившемся. Под установившемся режимом в данном случае понимается разработка траншеи с постоянными скоростями движения всех его элементов, в частности, с постоянной частотой вращения рабочего органа и постоянной скоростью подачи инструмента на забой. В случае установившегося режима проходки левая часть уравнений движения (2) обращается в ноль, что приводит эти зависимости к статическому виду, то есть к равенству активных сил и моментов, соответствующих силам и моментам сопротивлений. С учетом принятых допущений система (2) для случая установившегося движения принимает вид:
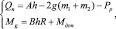 (3)
(3)
Выделив из второго уравнения системы (3) значение толщины стружки и подставив его в первое уравнение, получено
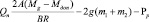 . (4)
. (4)
Полученное выражение позволяет определять усилие подачи инструмента на забой в зависимости от крутящего момента привода фрезы, грунтовых условий и конструктивных параметров фрезы в случае разработки грунта с постоянными скоростями движения элементов инструмента.
Фрезерный рабочий орган предназначен в основном для работы в грунтах, обладающих однородной структурой. В этих условиях процесс разрушения грунта фрезой носит установившийся стабильный характер. При изменении грунтовых или технологических условий регулирование режима производится ступенчато, в пределах одной проходки. Таким образом, в общем случае при определении и анализе движения инструмента и действующих на него нагрузок применен статический расчет механизма.
В ряде же случаев установившегося движения, а тем более при неустановившемся движении, имеющим место в период пуска или разгона фрезерного рабочего органа, эти расчеты недостаточны. Далее рассмотрены случаи работы исследуемого инструмента в условиях непостоянства рабочих скоростей.
Предварительно отмечено, что продолжительность пуска (разгона) рабочего органа, как показала практика, не превышает 3 секунд, что в сравнении с продолжительностью рабочего цикла (около 10 мин) в пределах.
Одной проходки весьма незначительная величина. Кроме того, период пуска в значительной степени зависят от квалификации машиниста, так как регулирование режима исследуемого рабочего органа производится вручную. Нарастание нагрузок на элементы конструкции в период пуска происходит линейно, по треугольнику. Таким образом, в связи с незначительностью периода пуска изменение режима в этот момент не представляет интереса.
В случае разработки траншеи с переменными рабочими скоростями рабочего органа, что имеет место при разработке разнородных грунтов в пределах одной проходки, расходуется (при увеличении скоростей) или поглощается (при уменьшении скоростей) энергия, равная работе сил инерции всех неравномерно движущихся масс (4). Фрезерный рабочий орган обладает двумя степенями свободы, и, следовательно, изменение режима возможно за счет изменения скорости поступательного перемещения инструмента или частоты вращения фрезы. Составлено для рассматриваемого случая уравнение динамического равновесия
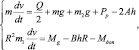 (5)
(5)
где 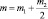 – приведенная масса одной фрезы и транспортера.
– приведенная масса одной фрезы и транспортера.
Интегрируя уравнения системы (5), можно определить скорости элементов фрезерного рабочего органа в периоды неустановившегося движения, а также продолжительность этих периодов. Однако, для того, чтобы провести интегрирование в конечном виде, необходимо знать закон изменения избыточных усилий и моментов в механизмах привода рабочего органа. В связи с новизной конструкции фрезерного инструмента указанный закон неизвестен и для его определения необходимы специальные исследования.
Для приближенного решения системы уравнений (5), допустимого в рамках данных исследований, представлено в виде
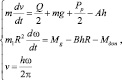 (6)
(6)
Третье уравнение системы (6) представляет собой кинематическую зависимость, связывающую угловую скорость, толщину стружки и скорость. Оно линеаризует систему (6) при условии, что значение является усредненным за весь процесс разрушения грунта фрезерным инструментом. Данное утверждение следует считать допущением, которое обосновывается тем, что в течение рабочего цикла фреза совершает значительное количество оборотов вокруг собственной оси (свыше 500). При этом каждому обороту соответствует своя толщина стружки, измеренная в направлении вертикальной оси. Эта величина может изменяться в большую или меньшую сторону, однако, при достаточно большом промежутке времени рабочего цикла, толщина срезаемой стружки стремится к среднему значению. С известным приближением принятое допущение можно представить в виде:
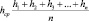 , (7)
, (7)
где n – количество оборотов инструмента за рабочий цикл.
Результаты исследования и их обсуждение
Представленная методика разработки уравнений движения фрезерных рабочих органов использовалась при определении режимных и силовых параметров указанных механизмов на стадии их рабочего проектирования на кафедре «Строительные и дорожные машины» Карагандинского государственного технического университета [6].
Выводы
Результаты исследования математической модели позволяют сделать следующие выводы:
– разработана и исследована математическая модель движения фрезерных рабочих органов, применяемых для проходки траншей и для рыхления мерзлых грунтов;
– установлены детерминированные зависимости, определяющие усилие подачи и крутящий момент, действующие на рабочий орган в зависимости от условий работы, сопротивления грунта разрушению, кинематических параметров режимов работы.

