Нейтроны средних энергий используются в медицинской физике для тяжёлых ядер с А~200 , физике космических лучей, где они создают фон, на котором проводятся измерения нейтринных обсерваторий [1]. Для сцинтилляционных детекторов нейтринных обсерваторий основной реакцией, создающей фон является реакция 12С(n,p)12B. В то же время расчёт таких реакций представляет определённую проблему, что отмечено в описании стандартных профессиональных программ ядерной физики, например программы TALYS, новые версии которой (например TALYS 1.6) не могут справиться с расчётами реакций с элементами группы углерода и более лёгких элементов. Поэтому, в программу заложено ограничение на атомный вес элементов A>12.
Последний эксперимент в этой области был выполнен группой n-TOF в ЦЕРН [2]. Полученное в этом эксперименте среднее сечение является аномально большим
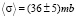. (1)
Это сечение примерно на порядок превосходит предсказанное моделированием на ранних версиях программы TALYS, с которым в [2] хорошее совпадение в пороговой области реакции. Полученный n-TOFF результат заменяет собой более ранние результаты (в частности [3] σ = 5mb), которые используются сегодня для расчёта фонов нейтринных обсерваторий.
Так как в эксперименте [2] были исследованы новые диапазоны энергий E = 100 MeV – 10 GeV, результат (1) приобретает смысл результата зондирующего эксперимента, за которым может скрываться новая физика.
Прямой аналитический расчёт сечения реакции
n + 12 C = p + 12 B (2)
может быть выполнен с помощью стандартных методов ядерной физики ( например с помощью метода треугольных диаграмм И.С. Шапиро [4]).В случае несовпадения результатов расчёта с экспериментом [2], он может быть скорректирован в рамках новых теоретических идей. Полное сечение прямой ядерной реакции в предлагаемой картине может быть рассчитано по формуле
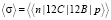(3)
В случае нелокальности ядерного взаимодействия [5,6] внешнее усреднение означает усреднение по конечным размерам ядра. Внешние обкладки амплитуды (3)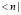 
, 
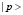соответствуют рассеиваемым нейтронам и выходящим из области реакции протонам. Амплитуды рассеяния этих частиц на ядре должны вычисляться с учётом нелокальности ядерного взаимодействия для лёгких ядер. Соответствующее этим процессам нелокальное уравнение Шредингера (НУШ) для ядра характерного размера β есть [7]:
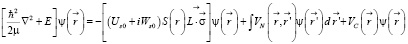(4)
где
μ – приведённая масса нуклона,
сепарабельный нелокальный ядерный потенциал Перри – Бака [6] имеет вид
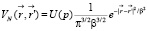(5)
Us0, Ws0,U(p) выражается через формы типа Пешля – Теллера, принятые для локального оптического потенциала ядра [6, 7].
Vc – несущественный для рассматриваемой задачи кулоновский потенциал ядра.
Для ядра конечных размеров положение точки ядра задаётся вектором
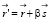(6)
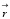– положение центра масс ядра, 0 < s < 1.
Перепишем для удобства НУШ в виде:
,
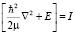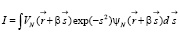(7)
Функции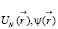 
гладкие [7] и экспоненциально быстро спадают с расстоянием (что естественно для ядерного потенциала). Поэтому, их можно локализовать, приближая разложением в ряд Тейлора по s.
Будем считать ядерное взаимодействие в первом приближении сферически симметричным. Зафиксируем точку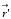 
на ядре.
Тогда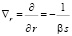 
Дифференцируя [7] по r превращаем его в принятом приближении в дифференциальное уравнение 3-го порядка:
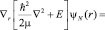
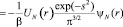(8)
Перейдём к стандартным обозначениям математической физики, и выполним дифференцирование в левой части [8]. Получается дифференциальное уравнение 3-го порядка для функции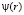 
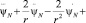
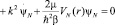, (9)
где обозначение «.» соответствует производной по радиальной переменной r,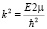 
.
Уравнение (9) является сингулярно – возмущённым по параметру kr>>1, что позволяет найти его решение в этом приближении. Условие kr>>1 соответствует для систем сферической геометрии квантовомеханическому приближению VKB. Отбрасывая по приведённому выше условию производные 2-го и 3-го порядка по r, найдём неосциллирующее гладкое решение уравнения (9).
Получаем
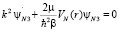(10)
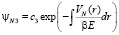(11)
Из (11) видно, что это решение не имеет предельного перехода к локальной теории ядра β → 0. Это решение, очевидно, соответствует общему потенциальному фону нелокальных ядерных сил. На квантовом языке такой фон соответствует поляризации вакуума или выпадению конденсата ядерных сил..
Найдём 2 осциллирующих решений уравнения (9). Выполняя замену
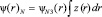, (12)
Получаем уравнение 2-го порядка для переменной z.
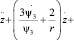
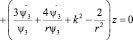(13)
Или
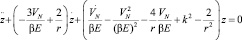(14)
Найдём асимптотическое решение (14) в виде:
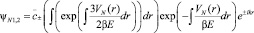(15)
где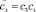 
Зафиксируем потенциал VN (r) на краю потенциальной ямы VN = VN (r)max = const. Это физически оправдано, так как рассматривается приближенное решение уравнения для функции ψ(r) при высоких энергиях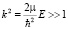 
(E>>1MeV). То.есть, пороговое значение 
.
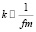Тогда для осциллирующих решений получаем
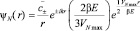(16)
При E → 0, β → 0 (т.е. в локальной квантовой механике) решение (16) не существует, т.к. выражение βE является математической неопределённостью.
Расходящаяся волна от рассеиваемой частицы имеет вид:
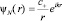, (17)
Изменение эвклидового фона за счёт выпадающего конденсата ядерных сил,
вследствие их нелокальности даётся множителем
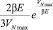(18)
Итоговая плотность вероятности нуклонного рассеяния с учётом изменения фона реакции за счёт выпавшего конденсата есть:
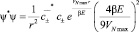(19)
Сечение рассеяния нуклонов на нелокальном потенциале выражается черезрешение (17). В этом случае, дифференциальное сечение рассеяния, соответствующее внешним обкладкам реакции (3) имеет вид:
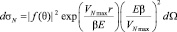(20)
Благодаря тому, что начальный и конечный нуклон рассеиваются на фоне, созданном нелокальным конденсатом ψ3 (11), величина сечения может вырасти или уменьшиться. Будем считать, что сечение рассеяния нуклонов (внешние обкладки амплитуды) (3) сферически симметричны, а зависящая от угла часть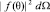 
принадлежит ядерной реакции и вычисляется по формулам прямой ядерной реакции.
Тогда формула сечения ядерной реакции факторизуется и принимает вид:
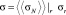(21)
Усредним по размерам ядра 0 < r < β нелокальную часть сечения (18) σN (r) Обозначим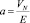 
, 
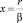. Этот результат получен при фиксации положения точки 
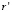на ядре.
Для получения числового значения сечения надо привести сечение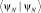 
к форме, имеющей предельный переход к локальной теории ядерных сил без особенности при точечных размерах ядра в пределе β → 0. Для нахождения этой величины произведём усреднение сечения ядра по его конечным размерам с помощью формулы
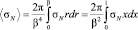(22)
Вычисляя интеграл (22), получаем
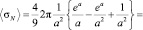
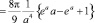(23)
Значение сечения реакции (3)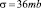 
приблизительно в A = 10 раз выше, чем предсказывает локальная теория. Посмотрим, допускает ли построенная теория такие значения сечения. То есть, выясним может ли в построенной теории нелокальный множитель 
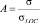иметь значение A = 10?
Для этого решим трансцендентное уравнение
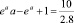(24)
Физический смысл множителя а – отношение высоты потенциального барьера к энергии внешних нуклонов.
При a<<1 уравнение (24) имеет аналитический корень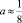 
. То есть, такое решение существует. Приближённые действительные положительные корни (24) равны a ≈ 0,43, а ≈ 7,45. Отсюда можно сделать вывод, что в рассматриваемом оценочном расчёте и при оговоренных выше приближениях основной вклад в факторизованную часть сечения, связанную с рассеянием нейтронов на фоне конденсата ядерных сил вносят энергии начальных нуклонов Е как выше, так и ниже барьера ядерных сил Vn.