Возможность образования упорядоченных литийсодержащих сплавов при электрохимическом окислении-восстановлении электродов на основе сплавов лития с металлами в обратимых источниках тока с апротонными растворами электролитов [1, 2]. В [3 – 6] предложена структурная модель электрохимического внедрения лития в металлы и сплавы из апротонных растворов электролитов. Структурно-комбинаторный анализ возможных структур электродных материалов на основе интерметаллических сплавов состава LixMe (0<x<4,5; Me = Sn, Pb) основан на использовании для моделирования структурного фрагмента состава LiMe с сответствующими дополнениями фрагментом Lix-1Me [7]. В результате моделирования образуются структуры гибридных фаз кристаллографического сдвига в случае сплавов вида LixMe.
Моделирование возможных структур сплавов
Исходной структурой для моделирования использовали структуру кубического CsCl (Pm3m, z = 1). Учитывая, что структуры упорядоченных сплавов LiSn и LiPb описываются структурой ромбоэдрически искаженного CsCl (структурный тип b’-SbSn, R`3m, z = 6 в гексагональной установке), рассматривали влияние действия одномерного кристаллографического сдвига на стехиометрию слоев в плоскости (110) ромбоэдрической фазы и стехиометрию образующихся гомологических фаз Lian-bMen. Установлено закономерное изменение периода идентичности в структурах гомологов ряда Li5n-3Men в направлении нормали к плоскостям кристаллографического сдвига. В результате моделирования получено две серии гомологических рядов интерметаллических литийсодержащих фаз [3, 4]. Результаты идентификации кристаллических структур одного из этих рядов – гомологов ряда Li5n-3Men (n = 2 – 6, ∞) [4] представлены в таблице, а их изображения – на рисунке.
Результаты моделирования структур интерметаллических сплавов в системах Li-Me подтверждаются известными экспериментальными данными, полученными в системах Li – Sn и Li – Pb: упорядоченные сплавы Li2Pb, Li2Sn с ромбоэдрическими структурами (P`3m1) [8 – 11].
Упорядоченные структуры сплавов гомологической серии Li5n-3Men
|
Номер гомолога |
Состав |
Пространственная группа (число формульных единиц в элементарной ячейке) |
Кристаллографические позиции для атомов |
Относительные метрические параметры элементарной ячейки |
|
1 |
Li2 Me |
P`3m1 (z = 1) |
Li: 2(d), Me: 1(a) |
a = a0, c = c0 |
|
2 |
Li7 Me2 |
P`3m1 (z = 1) |
Li:1(a)+2(c)+2*2(d), Me: 2(d) |
a = a0, c = 3c0 |
|
3 |
Li4 Me |
P`3m1 (z = 3) |
Li: 2*2(c)+4*2(d), Me:1(a)+2(d) |
a = a0, c = 5c0 |
|
4 |
Li17 Me4 |
C2/m (z = 4) |
Li: 17*4(i), Me: 2(a)+2(b)+ 2*4(i) |
a = 31/2a0, b = a0 c = 14c0, b = 900 |
|
5 |
Li22 Me5 |
C2/m (z = 2) |
Li: 11*4(i), Me: 2(a)+2*4(i) |
а= 31/2a0, b = a0 c = 9c0, b = 900 |
|
6 |
Li9 Me2 |
C2/m (z = 2) |
Li: 2(b)+4*4(i), Me: 2(a)+2(d) |
a = 31/2a0, b = a0 c = 7,67c0, b = 850 |
|
¥ |
Li5 Me |
P`3m1 (z = 4) |
Li: 4(b)+2*8(c), Me: 4(a) |
a = a0, c = 2c0 |
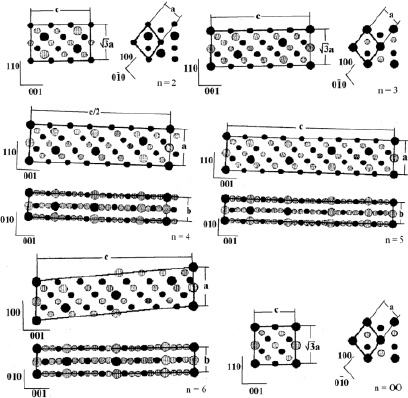
Изображения структур членов гомологического ряда Li5n-3Men. Слева направо химический состав Li7Me2 (n = 2), Li4Me (n = 3), Li17Me4 (n = 4), Li22Me5 (n = 5), Li9Me2 (n = 6) и Li5Me (n = ∞)
Однако структуры реально существующих сплавов с составами Li5n-3Men (при n ≥ 3) уже не могут быть описаны как гомологи одномерного ряда [6]. Структуры Li22Sn5 и Li22Pb5 – кубические (F23), а не моноклинные (C2/m), как это следует из предположения об одномерности кристаллографического сдвига [3 – 6]. Высказанное в работах [4, 6] предположение о повышении мерности кристаллографического сдвига от единицы до двух или трех для структур реально существующих фаз (возможных структурных гомологов двумерных или трехмерных гомологических рядов) косвенно подтверждается изменением характера концентрационной зависимости плотности сплавов LixMe (Me = Sn, Pb) при x ≈ 3,5 [12].
Полученные результаты подтверждаются структурными данными для известных интерметаллических сплавов до второго гомолога ряда Li5n-3Men. Для структур сплавов этого ряда с порядковым номером n ≥ 3 топологический параметр k становится меньше, чем (1+t) и не соответствует ограничениям (1+t) < k < (2+t) (t – численное выражение золотого сечения) [7]. Данный факт также косвенно подтверждается изменением характера концентрационной зависимости плотности сплавов LixSn при x @ 3,5 и существенными энергетическими затратами на зарядной кривой.
Отметим, что методика формирования одномерного гомологического ряда подобна методике, разработанной для одномерных гомологических рядов оксидов металлов с октаэдрическими структурами [13, 14]. Представленная модель структурообразования литийсодержащих сплавов может быть использована при анализе механизма образования структур упорядоченных фаз в системах, где возможно проявление структурной гомологии.

