Введение
В последние три десятилетия наблюдается бурное развитие информационных технологий и их внедрение в самые различные сферы деятельности человека, и информация, представленная в электронном виде, стала ключевой частью жизни и работы не только организаций, но и каждого отдельного человека. Более того, сохранность и доступность информации для ее пользователей, как правило, имеет критическую важность, а потеря данных нередко может приводить к катастрофическим последствиям. В такой ситуации анализ показателей надежности дисковых массивов имеет достаточно высокую актуальность, особенно для предприятий среднего и крупного масштабов, поскольку такой анализ также позволяет оценивать риски потери данных и принимать соответствующие решения, и при необходимости внедрять дополнительные технические средства.
В настоящее время существует множество вариантов построения дисковых хранилищ с применением одного или нескольких дисковых массивов по той или иной технологии RAID (Redundant Array of Inexpensive Disks), причем как классических (RAID-0, RAID-1, RAID-5, RAID-6), так и каскадных (RAID-10, RAID-50, RAID-60, RAID-51, RAID-61), матричных и других специализированных видов массивов.
С целью достижения высокой отказоустойчивости (особенно для баз данных), как правило, применяются RAID-1 массивы (также известные как «зеркало»), в котором все диски хранят одни и те же данные, и массив сохраняет работоспособность до тех пор, пока хотя бы один диск работоспособен. В силу высоких накладных расходов (при любом количестве дисков полезная емкость массива всегда равна емкости одного диска), на практике, как правило, используют двухдисковый RAID-1 массив.
Что касается моделей надежности, то с одной стороны имеется ряд академических учебников по теории надежности [1, 2], в которых рассматриваются обобщенные модели надежности технических систем, но нет конкретных примеров по современным системам хранения данных, в частности, избыточным дисковым массивам. С другой стороны имеется специализированная литература [3], посвященная надежности вычислительных машин, систем и сетей, в которых рассматриваются дисковые массивы, но приведенные модели надежности слишком упрощены и дают завышенные значения для показателей надежности.
Соответственно, в рамках научных исследований автора в области надежности систем [4-10] возникла научная задача разработки специализированной модели надежности для двухдискового массива RAID-1, для последующего использования полученных результатов при проектировании систем хранения данных для промышленных предприятий.
Базовая модель надежности двухдискового массива
Рассмотрим сначала известную упрощенную модель надежности двухдискового массива на базе модели дублированной системы с двумя с независимыми элементами.
Введем следующее множество состояний двухдискового массива RAID-1 и условий переходов из одного состояния в другое:
Состояние 0 (online) – оба диска исправны, данные массива доступны. Из этого состояния массив может с интенсивностью 2λD (отказ любого из исправных дисков) перейти в состояние 1.
Состояние 1 (degraded) – один диск исправен, другой диск отказал. Из этого состояния массив может с интенсивностью λD (отказ оставшегося диска) перейти в состояние 2, либо с интенсивностью μD (замена отказавшего диска и репликация данных с оставшегося диска) в состояние 0.
Состояние 2 (offline) – оба диска отказали, и массив разрушен.
где, λD – интенсивность отказов дисков в исправном состоянии.
μR – интенсивность замены диска и репликации данных.
Ниже на рис. 1 приведена марковская цепь, отражающая множество состояний системы и условия переходов:
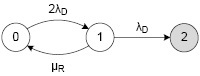
Рис. 1. Базовая модель надежности двухдискового массива RAID-1
Соответственно, система дифференциальных уравнений Колмогорова-Чепмена для этой цепи выглядит следующим образом:
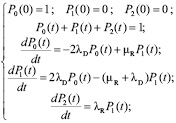(1)
Тогда, учитывая, что состояние 0 является начальным, а состояние 2 – финальным, при котором массив разрушается, и теряются данные, мы имеем следующую формулу для расчета среднего времени наработки массива до потери данных:
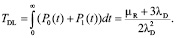(2)
Усовершенствованная модель надежности двухдискового массива
Теперь рассмотрим предлагаемую автором модель надежности двухдискового массив RAID-1 с учетом конечного времени обнаружения и замены вышедшего из строя диска, конечного времени репликации данных (процедура rebuild) на замененном диске, возможности отказа как оставшегося диска, так реплицируемого диска, а также возможности срыва процедуры репликации из-за ошибки чтения данных с оставшегося диска.
Введем следующее множество состояний двухдискового массива RAID-1 и условий переходов из одного состояния в другое:
Состояние 0 (online) – оба диска исправны, данные массива доступны. Из этого состояния массив может с интенсивностью 2λD (отказ любого из исправных дисков) перейти в состояние 1.
Состояние 1 (degraded) – один диск исправен, другой диск отказал и ожидает замены, данные массива доступны. Из этого состояния массив может с интенсивностью λD (отказ исправного диска) перейти в состояние 2, либо с интенсивностью μD (замена отказавшего диска) в состояние 3.
Состояние 2 (offline 2) – оба диска отказали, и массив разрушен.
Состояние 3 (rebuild) – один диск исправен, другой диск заменен, на замененном диске идет репликация данных с исправного диска, данные массива доступны. Из этого состояния массив может с интенсивностью μR (завершение репликации данных на замененном диске) перейти в состояние 0, либо с интенсивностью λR (отказ реплицируемого диска) в состояние 1, либо с интенсивностью λD (отказ исправного диска) в состояние 4, либо с интенсивностью εD (критическая ошибка чтения данных исправного диска в процессе репликации) в состояние 5.
Состояние 4 (offline 1) – один из ранее отказавших дисков заменен, но данные на него не успели реплицироваться, так как другой диск, с которого выполнялась репликация данных, отказал, и массив разрушен.
Состояние 5 (offline 0) – оба диска исправны, но произошла ошибка при репликации данных на замененный диск, и массив разрушен.
где, λD – интенсивность отказов дисков в исправном состоянии.
μD – интенсивность замены отказавшего диска.
λR – интенсивность отказов при репликации или восстановлении данных на замененный диск (большой объем операций записи).
μR – интенсивность восстановления или репликации данных.
εD – интенсивность ошибок чтения данных исправного диска при репликации данных на другой диск (большой объем операций чтения).
Ниже на рис. 2 приведена марковская цепь, отражающая множество состояний системы и условия переходов.
Соответственно, система дифференциальных уравнений Колмогорова-Чепмена для этой цепи выглядит следующим образом:
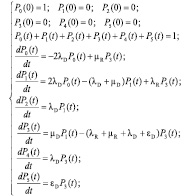(3)
Тогда, учитывая, что состояние 0 является начальным, а состояния 2, 4 и 5 – финальными, при котором массив разрушается, и теряются данные, мы имеем следующую формулу для расчета среднего времени наработки до потери данных:
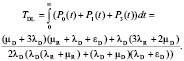(4)
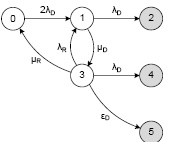
Рис. 2. Усовершенствованная модель надежности двухдискового массива RAID-1
Оценка исходных параметров надежности дисков и массива. Интенсивность отказов дисков λD можно оценить на основе параметра MTTF (Mean Time To Failure), предоставленного производителем дисков или полученного из практического опыта эксплуатации. Следует отметить, что производители часто завышают MTTF, указывая более миллиона часов. Практика же показывает, что MTTF диска лежит в пределах 50-300 тысяч часов. Что касается интенсивности отказов в режиме репликации (восстановления) данных λR, то в силу большого объема операций записи интенсивность отказов реплицируемого диска выше базовой интенсивности. Мы будем упрощенно полагать, что интенсивность реплицируемого диска втрое выше:
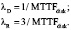(5)
Интенсивность замены диска зависит от того, происходит ли замена автоматически за счет применения дополнительных дисков (помимо основных дисков в массиве) и технологии горячего резерва, или же обнаружения и замена диска осуществляется специалистами. В первом случае замена может занимать несколько минут, во втором – несколько часов. Соответственно, обобщая оба случая можно сказать, что интенсивность замены определяется параметром MTWS (Mean Time Waiting for Spare):
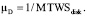(6)
Интенсивность репликации данных μR для массивов RAID-1 зависит от емкости диска V (в байтах), средней скорости записи νWR на диск (в байт/сек) и средней скорости чтения νRD данных (в байт/сек), и может быть оценена следующим образом:
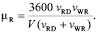(7)
Например, для диска емкости 1012 байтов, скорости записи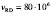 
байт/сек и скорости чтения 
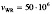байт/сек, интенсивность репликации данных составит 
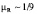час-1 (в среднем репликация данных длится 9 часов).
Интенсивность ошибок чтения εD диска можно определить на основе параметра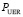 
(вероятности невосстанавливаемой ошибки чтения бита), предоставленного производителем дисков или полученного из практического опыта эксплуатации, емкости диска V (в байтах) и среднего времени репликации данных, равного 1/μR (в часах). Для дисков персональных компьютеров 
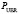составляет ~10-14, для дисков серверных систем ~10-15.
Тогда, учитывая, что при репликации данных в массиве RAID-1 требуется считывать весь диск размером 8V битов, то вероятность ошибки чтения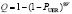 
. С другой стороны полагая, что время наработки на ошибку – экспоненциально распределенная случайная величина с параметром εD, и регенерация длится в течение 1/μR часов, имеем равенство 
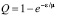. Тогда, из двух тождеств получаем 
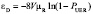. Тогда, учитывая, что 
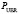очень малая величина, и 
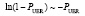, окончательно получаем:
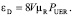(8)
Например, для диска емкости V = 1012 байтов, интенсивности репликации данных μR = 1/9 час-1 и вероятности невосстанавливаемой ошибки чтения бита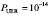 
, интенсивность ошибок чтения составит εD ≈ 1/112 час-1.
Пример расчета
Имеется массив RAID-1 с двумя дисками емкостью V = 1012 байтов. Среднее время наработки до отказа диска составляет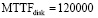 
часов. Интенсивность отказов реплицируемого диска втрое выше. Вероятность невосстанавливаемой ошибки чтения бита 
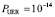. Средняя скорость чтения данных 
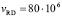байт/сек. Средняя скорость записи данных 
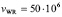байт/сек. Среднее время замены дисков 
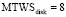часов.
Оценим сначала исходные параметры надежности по формулам 5-8.
Интенсивность отказов диска:
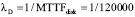час-1.
Интенсивность отказов реплицируемого диска: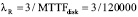 
час-1.
Интенсивность замены дисков: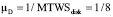 
час-1.
Интенсивность репликации данных в массиве: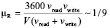 
час-1.
Интенсивность ошибок чтения при репликации: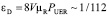 
час-1.
Рассчитаем среднее время наработки до потери данных дискового массива по известной упрощенной модели (формула 2):
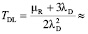800180000 часов.
Теперь рассчитаем среднее время наработки до потери данных дискового массива по предложенной автором модели (формула 4):
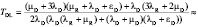
805522 часа.
Нетрудно заметить, что специализированная модель, учитывающая ряд дополнительных параметров надежности дисков и массива, дает значительно более низкую и реалистичную оценку среднего времени наработки массива RAID-1 до потери данных, нежели чем известная упрощенная модель.
Заключение
Таким образом, в рамках данной статьи рассмотрены двухдисковый массив RAID-1, известная упрощенная модельная надежности и предложенная автором специализированная модель надежности для расчета среднего времени наработки массива до потери данных. Также рассмотрены методика оценки исходных параметров надежности дисков и массива, и приведен пример расчета среднего времени наработки.
Полученные научные результаты использовались автором при проектировании систем хранения данных для НИУ МЭИ (ТУ), Балаковской АЭС, ОАО «Красный Пролетарий» и ряда других предприятий.