Scientific journal

International Journal of Applied and fundamental research

ISSN 1996-3955

ИФ РИНЦ = 0,593

Введение

Для вычисления функций используются степенные, рациональные и другие разложения, а также дифференциальные уравнения [1, 2].

Многие методы решения дифференциальных уравнений переводятся на язык клеточных автоматов, где допускают дальнейшее развитие, приобретают наглядную форму, удобную для вычислений и программирования.

В статье показано создание клеточных автоматов для приближенного вычисления некоторых функций. На основе этих клеточных автоматов можно создать программы для приближенного вычисления соответствующих функций. Делается сравнение клеточных автоматов по точности вычисления.

Клеточные автоматы изучаются и используются в математике, теории вычислимости, физике, теоретической биологии, микромеханике. Применение клеточных автоматов для приближенного вычисления функций в литературе не обнаружено.

Клеточные автоматы для приближенного вычисления y(x)=lnx

Составим из первой и второй производных функции y(x)=lnx обыкновенное дифференциальное уравнение 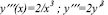(1).

(1)

Чтобы найти решение уравнения (1), удовлетворяющее условиию y(x₀)=lnx₀, делим интервал (x₀, x_m] на m промежутков длины ∆x=(xm–x₀)/m и, заменяя y'(x)≈∆y/∆x, y x)≈∆²y/∆x², получаем разностное уравнение (2)

(y_k+2−2y_k+1+y_k)/∆x²=−((y_k+1−y_k)/∆x)²

(k=0,1,…,m−2; ∆x=(x_m–x₀)/m) (2)

с дополнительными условиями y₀=lnx₀, y₁=ln(x₀+∆x). Равенство (2) эквивалентно (3), которое формально совпадает с определением клеточного автомата.

y_k+2=2y_k+1−y_k−(y_k+1−y_k)² (3)

Для решения уравнения (1) можно получить другое разностное уравнение (4), если ∆y заменить на y_k−y_k−1

(y_k+2−2y_k+1+y_k)/∆x²=−((y_k−y_k−1)/∆x)²

(k=1,2,…,m−2; ∆x=(x_m–x₀)/m) (4)

с дополнительными условиями y₀=lnx₀, y₁=ln(x₀+∆x), y₂=ln(x₀+2∆x). Равенство (4) эквивалентно (5), которое формально совпадает с определением клеточного автомата.

y_k+2=2y_k+1−y_k−(y_k−y_k−1)² (5)

Составим из первой и третьей производных функции y(x)=lnx обыкновенное дифференциальное уравнение (6).

Y’’’(x)=2/x³ ; y’’’=2y’³ (6)

Чтобы найти решение уравнения (6), удовлетворяющее условию y(x₀)=lnx₀, делим интервал (x₀, x_m] на m промежутков длины ∆x=(x_m–x₀)/m и, заменяя y’(x)≈∆y/∆x, y’’’(x)≈∆³y/∆x³, получаем разностное уравнение (7)

(y_k+3−3y_k+2+3y_k+1−y_k)/∆x³=2((y_k+1−y_k)/∆x)³

(k=0,1,…,m−3; ∆x=(x_m–x₀)/m)(7)

с дополнительными условиями y₀=lnx₀, y₁=ln(x₀+∆x), y₂=ln(x₀+2∆x). Равенство (7) эквивалентно (8), которое формально совпадает с определением клеточного автомата.

y_k+3=3y_k+2−3y_k+1+y_k+2(y_k+1−y_k)3 (8)

В табл. 1 приведены отличия между y(x)=lnx и клеточными автоматами (3), (5), (8) при разных значениях m, x₀=1, x_m=2.

Таблица 1

Отличия между y(x)=lnx и клеточными автоматами (3), (5), (8) при разных значениях m, x₀=1, x_m=2

Наименьшие отличия у клеточного автомата (3). Сдвиг по ∆y дал клеточный автомат (4), у которого отличия увеличились. Использование третьей производной функции дало клеточный автомат (8), у которого наибольшие отличия. Увеличение m уменьшает отличие.

Клеточные автоматы для приближенного вычисления y(x)=sinx. Составим из функции y(x)=sinx и ее производной обыкновенное дифференциальное уравнение (9).

y’(x)=cosx=(1−sin²x)^1/2 ; y’=(1−y²)^1/2 (9)

Чтобы найти решение уравнения (4), удовлетворяющее условию y(x₀)=sinx₀, делим интервал (x₀, x_m] на m промежутков длины ∆x=(x_m–x₀)/m и, заменяя y’(x)≈∆y/∆x, получаем разностное уравнение (10)

(y_k+1−y_k)/∆x=(1−y_k²)^1/2

(k=0,1,…,m−1; ∆x=(x_m–x₀)/m) (10)

с дополнительным условием y₀=sinx₀. Равенство (10) эквивалентно (11), которое формально совпадает с определением клеточного автомата.

y_k+1=y_k+∆x(1−y_k²)^1/2 (11)

Для решения уравнения (9) можно получить другое разностное уравнение (12), если y заменить на y_k−1

(y_k+1−y_k)/∆x=(1−y_k−1²)^1/2

(k=1,2,…,m−1; ∆x=(x_m–x₀)/m) (12)

с дополнительными условиями y₀=sinx₀, y₁=sin(x₀+∆x). Равенство (12) эквивалентно (13), которое формально совпадает с определением клеточного автомата.

y_k+1=y_k+∆x(1−y_k−1²)^1/2 (13)

Составим из функции y(x)=sinx и ее второй производной обыкновенное дифференциальное уравнение (14).

y’’(x)=−sinx ; y’’=−y (14)

Чтобы найти решение уравнения (14), удовлетворяющее условию y(x₀)=sinx₀, делим интервал (x₀, x_m] на m промежутков длины ∆x=(x_m–x₀)/m и, заменяя y’’(x)≈∆²y/∆x², получаем разностное уравнение (15)

(y_k+2−2y_k+1+y_k)/∆x²=−y_k

(k=0,1,…,m−2; ∆x=(x_m–x₀)/m) (15)

с дополнительными условиями y₀=sinx₀, y₁=sin(x₀+∆x), y₂=sin(x₀+2∆x). Равенство (15) эквивалентно (16), которое формально совпадает с определением клеточного автомата.

y_k+2=2y_k+1−y_k(1+∆x²) (16)

В таблице 2 приведены отличия между y(x)=sinx и клеточными автоматами (11), (13), (16) при разных значениях m, x₀=0, x_m=1.

Таблица 2

Отличия между y(x)=sinx и клеточными автоматами (11), (13), (16) при разных значениях m, x₀=0, x_m=1

Наименьшие отличия у клеточного автомата (11). Сдвиг по ∆y дал клеточный автомат (13), у которого отличия увеличились. Использование второй производной функции дало клеточный автомат (16), у которого наибольшие отличия. Увеличение m уменьшает отличие.

Клеточные автоматы для приближенного вычисления y(x)=tgx. Составим из функции y(x)=tgx и ее производной обыкновенное дифференциальное уравнение (17).

y’(x)=1/cos²x=tg²x+1 ; y’=y²+1 (17)

Чтобы найти решение уравнения (17), удовлетворяющее условию y(x₀)=tgx₀, делим интервал (x₀, x_m] на m промежутков длины ∆x=(x_m–x₀)/m и, заменяя y’(x)≈∆y/∆x, получаем разностное уравнение (18)

(y_k+1−y_k)/∆x=y_k²+1

(k=0,1,…,m−1; ∆x=(x_m–x₀)/m) (18)

с дополнительным условием y₀=tgx₀. Равенство (18) эквивалентно (19), которое формально совпадает с определением клеточного автомата.

y_k+1=y_k+∆x(y_k²+1) (19)

Для решения уравнения (17) можно получить другое разностное уравнение (20), если y заменить на y_k−1

(y_k+1−y_k)/∆x=y_k−1²+1

(k=1,2,…,m−1; ∆x=(x_m–x₀)/m) (20)

с дополнительными условиями y₀=tgx₀, y₁=tg(x₀+∆x). Равенство (20) эквивалентно (21), которое формально совпадает с определением клеточного автомата.

y_k+1=y_k+∆x(y_k−1²+1) (21)

Составим из функции y(x)=tgx и ее второй производной обыкновенное дифференциальное уравнение (22).

y’’(x)=2tgxsec²x=2(tg³x+tgx) ; y’’=2(y³+y) (22)

Чтобы найти решение уравнения (22), удовлетворяющее условию y(x₀)=tgx₀, делим интервал (x₀, x_m] на m промежутков длины ∆x=(x_m–x₀)/m и, заменяя y’’(x)≈∆²y/∆x², получаем разностное уравнение (23)

(y_k+2−2y_k+1+y_k)/∆x²=2(y_k³+y_k)

(k=0,1,…,m−2; ∆x=(x_m–x₀)/m) (23)

с дополнительными условиями y₀=tgx₀, y₁=tg(x₀+∆x). Равенство (23) эквивалентно (24), которое формально совпадает с определением клеточного автомата.

y_k+2=2y_k+1−y_k+2∆x²(y_k³+y_k) (24)

В табл. 3 приведены отличия между y(x)=tgx и клеточными автоматами (19), (21), (24) при разных значениях m, x₀=0, x_m=1.

Наименьшие отличия у клеточного автомата (19). Использование второй производной функции дало клеточный автомат (24), у которого отличия увеличились. Сдвиг по ∆y дал клеточный автомат (21), у которого наибольшие отличия. Увеличение m уменьшает отличие.

Клеточные автоматы для приближенного вычисления y(x)=sin(lnx). Составим из первой и второй производных функции y(x)=sin(lnx) обыкновенное дифференциальное уравнение (25).

y’(x)=cos(lnx)/x ; y’’(x)=−(sin(lnx)+cos(lnx))/x² ;

y’’=− y’² (y/(1−y²)+1/(1−y²)^0.5) (25)

Чтобы найти решение уравнения (25), удовлетворяющее условиию y(x₀)=sin(lnx₀), делим интервал (x₀, x_m] на m промежутков длины ∆x=(x_m–x₀)/m и, заменяя y’(x)≈∆y/∆x, y’’(x)≈∆²y/∆x², получаем разностное уравнение (26)

(y_k+2−2y_k+1+y_k)/∆x²=−((y_k+1−y_k)/∆x)²

(y_k/(1−y_k²)+1/(1−y_k²)^0.5)

(k=0,1,…,m−2; ∆x=(x_m–x₀)/m) (26)

с дополнительными условиями y₀=sin(lnx₀), y₁=sin(ln(x₀+∆x)). Равенство (26) эквивалентно (27), которое формально совпадает с определением клеточного автомата.

y_k+2=2y_k+1−y_k−(y_k+1−y_k)²(y_k/(1−y_k²)

+1/(1−y_k²)^0.5) (27)

Для решения уравнения (25) можно получить другое разностное уравнение (28), если ∆y заменить на y_k−y_k−1

(y_k+2−2y_k+1+y_k)/∆x²=−((y_k−y_k−1)/∆x)²

(y_k/(1−y_k²)+1/(1−y_k²)^0.5)

(k=1,2,…,m−2; ∆x=(x_m–x₀)/m) (28)

с дополнительными условиями y₀=sin(lnx₀), y₁=sin(ln(x₀+∆x)), y₂=sin(ln(x₀+2∆x)). Равенство (28) эквивалентно (29), которое формально совпадает с определением клеточного автомата.

y_k+2=2y_k+1−y_k−(y_k−y_k−1)²(y_k/(1−y_k²)

+1/(1−y_k²)^0.5) (29)

Таблица 3

Отличия между y(x)=tgx и клеточными автоматами (19), (21), (24) при разных значениях m, x₀=0, x_m=1

Составим из первой и третьей производных функции y(x)=sin(lnx) обыкновенное дифференциальное уравнение (30).

y’’’(x)=(3sin(lnx)+cos(lnx))/x³ ;

y’’’=3yy’³/(1−y²)^1.5+ y’³/(1−y²) (30)

Чтобы найти решение уравнения (70), удовлетворяющее условию y(x₀)=sin(lnx₀), делим интервал (x₀, x_m] на m промежутков длины ∆x=(x_m–x₀)/m и, заменяя y’(x)≈∆y/∆x, y’’’(x)≈∆³y/∆x³, получаем разностное уравнение (31)

(y_k+3−3y_k+2+3y_k+1−y_k)/∆x³=

((y_k+1−yk)/∆x)³(3yk/(1−y_k²)^1.5+1/(1−y_k²))

(k=0,1,…,m−3; ∆x=(x_m–x₀)/m) (31)

с дополнительными условиями y₀=sin(lnx₀), y₁=sin(ln(x₀+∆x)), y₂=sin(ln(x₀+2∆x)). Равенство (31) эквивалентно (32), которое формально совпадает с определением клеточного автомата.

y_k+3=3y_k+2−3y_k+1+y_k+(y_k+1−y_k)³

(3y_k/(1−y_k²)^1.5+1/(1−y_k²)) (32)

В табл. 4 приведены отличия между y(x)=sin(lnx) и клеточными автоматами (27), (29), (32) при разных значениях m, x₀=1, x_m=2.

Таблица 4

Отличия между y(x)=sin(lnx) и клеточными автоматами (27), (29), (32) при разных значениях m, x₀=1, x_m=2

Наименьшие отличия у клеточного автомата (27). Сдвиг по ∆y дал клеточный автомат (29), у которого отличия увеличились. Использование третьей производной функции дало клеточный автомат (32), у которого отличия больше чем у клеточного автомата (27), за исключением m=10. Увеличение m уменьшает отличие, за исключением клеточного автомата (32) при m=10⁵.

Заключение

Для приближенного вычисления функции могут быть созданы различные клеточные автоматы. Источниками клеточных автоматов могут быть дифференциальные и разностные уравнения. Если на основе клеточного автомата требуется создать программу для приближенного вычисления функции, то рекомендуется использовать дифференциальное уравнение с минимальным порядком. Для повышения точности вычисления рекомендуется уменьшать шаг вычисления.