Электромагнитный привод колебательного движения используется в строительстве, машиностроении, горной технике, медицине и других отраслях промышленности. По существу, он представляет собой силовую электромагнитную импульсную систему, в которой генератором импульсов силы служит линейный электромагнитный двигатель. В конструкции двигателя содержится одно подвижное звено – якорь, совершающий возвратно-поступательное движение под действием электромагнитной тяговой силы и упругой силы сжимаемой пружины. В отличие от электрических машин вращательного движения линейный электромагнитный двигатель выполняется не в виде самостоятельного изделия, а компонуется с рабочей машиной (например, компрессором) как единое устройство определенного функционального назначения.
Исследования по разработке и созданию электромагнитного привода колебательного движения проводятся давно [1, 2], однако на современном уровне не все проблемы решены. Особенно актуальна проблема оптимального проектирования, связанная с поиском оптимальных режимов энергопреобразования и оптимальных конструкций линейных электромагнитных двигателей, учитывающих особенности рабочего процесса.
Развитие современных информационных технологий по исследованию электромагнитных полей с помощью комплекса программ «ELCUT» [3] позволяет существенным образом изменить состояние вопроса по совершенствованию методики оптимального проектирования электромагнитных двигателей и количественному анализу происходящих в них процессов энергопреобразования. Для достижения поставленной цели в данной статье использовано решение задачи оптимального управления электромагнитным приводом колебательного движения [4], полученное на приближенных моделях магнитного поля электромагнитного двигателя и их расчета аналитическими методами, каким является метод вероятных путей магнитного потока [5].
Задача оптимального управления электромагнитным приводом может быть рассмотрена как задача установления взаимосвязи между обобщенными параметрами импульсного источника питания (Uд, α, ωtк, f), линейного электромагнитного двигателя (a, m, ρ) и рабочей машины (Pм, 2хm), удовлетворяющей критерию оптимальности – максимуму КПД электромеханического преобразователя на заданный во времени закон движения якоря. Обобщенными параметрами импульсного источника питания являются Uд – максимальное значение напряжения на катушке, α – угол укорочения импульса напряжения, ωtк – фазовый угол сдвига между квадратом потокосцепления Ψ2(t) и законом движения якоря x(t) во времени; f – частота питающего напряжения; a – среднее значение инверсной индуктивности (величина обратная индуктивности) катушки на середине хода якоря; m – глубина модуляции инверсной индуктивности катушки; ρ = Ra/ω – добротность двигателя; ω = 2πf – угловая частота; R – активное сопротивление, учитывающее потери в катушке и стальном сердечнике; Pм – среднее значение мощности, передаваемой в механическую подсистему, 2хm – ход поршня компрессора.
При решении задачи оптимального управления зависимость инверсной индуктивности катушки двигателя от хода якоря электромагнитного двигателя представлена уравнением прямой линии
,
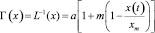где 0 ≤ x(t) ≤ 2∙хm – граничные значения хода якоря.
Такое допущение правомерно при выполнении инженерных расчетов ненасыщенных магнитных систем, в линейном электромагнитном двигателе оно справедливо на значительной части хода якоря, вследствие наличия большой величины рабочего зазора. Это обстоятельство позволяет получить аналитическое решение задачи оптимального управления, соответствующее максимально возможному КПД электромагнитного привода колебательного движения при заданном во времени законе движения якоря
,
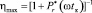где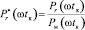 
– минимально возможные относительные потери в электромагнитном двигателе, Pr(ωtк) – мощность тепловых потерь, Pм(ωtк) – среднее значение мощности, передаваемой в механическую подсистему, ωtк – корень уравнения, определяемый условием поиска экстремума (минимума) функции 
.
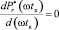Решение задачи управления для тока в катушке имеет вид:
,
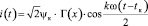Напряжения на участках эквивалентной схемы замещения электромагнитного двигателя, состоящей из последовательного соединения активного и индуктивного сопротивлений
,
.
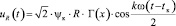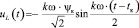Оптимальная форма импульсов напряжения источника питания определяется из уравнения электрического равновесия
.
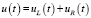Временная зависимость потокосцепления катушки
,
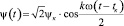где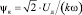 
– действующее значение потокосцепления, 
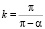– коэффициент скважности импульсов.
Приведенные математические выражения для тока, напряжений на участках схемы замещения линейного электромагнитного двигателя, оптимальной формы импульса источника питания и потокосцепления катушки справедливы на интервале времени – π + α + ωtк ≤ ωtк ≤ π – α + ωtк, вне этого интервала они обращаются в нуль.
В решении задачи оптимального управления заданный закон движения якоря в установившемся режиме есть несинусоидальная периодическая функция во времени. Если она задается табличным способом, то ее дальнейшее использование требует аппроксимации рядом Фурье
.
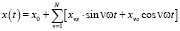При синусоидальном законе движения якоря х(t) = xm(1+ sin ωt) среднее значение мощности, поступающей в механическую подсистему, значительно упростится
.
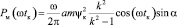Среднее значение мощности тепловых потерь при этом будет
.
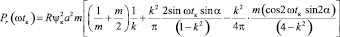Минимально возможные относительные потери определяются отношением средних значений мощностей
.
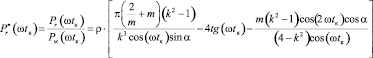Решение задачи оптимального управления определяет фазовый угол сдвига между квадратом потокосцепления Ψ2(t) и синусоидальным во времени законом движения якоря х(t) как корень тригонометрического уравнения
.
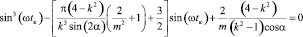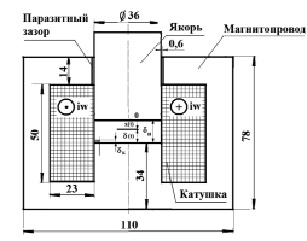
Рис. 1. Оптимальная конструкция линейного электромагнитного двигателя
Решение задачи оптимального управления положено в основу алгоритма проектирования линейных электромагнитных двигателей, имеющих максимально возможный КПД при удовлетворении условия минимума массы активных материалов, необходимых для его изготовления. Предложенный алгоритм реализован в программе «Анализ» на языке визуального программирования Borland Delphi 7.0 в среде Windows XP.
Демонстрацию основных возможностей программы «Анализ» рассмотрим на конкретном примере, в котором на предварительном этапе с помощью программы выполнен расчет основных геометрических размеров магнитной системы и обмоточных данных оптимальной конструкции линейного электромагнитного двигателя с использованием упрощенной модели магнитного поля, рассчитанной методом вероятных путей магнитного потока. На рис. 1 приведена оптимальная конструкция линейного электромагнитного двигателя, соответствующая техническому заданию, а именно: среднее значение мощности, поступающей в механическую подсистему Pм = 180 Вт, частота следования импульсов напряжения f = 50 Гц, синусоидальный во времени закон движения якоря х(t) = 5∙10–3(1 + sin 314t) м, коэффициент заполнения кз = 0,6, плотность тока в катушке J = 6∙106 А/м2, максимальное значение напряжения на катушке Uд = 27 В, угол укорочения импульса α = 30 град.
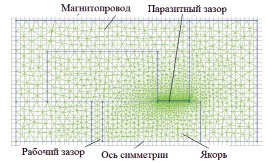
Рис. 2. Расчетная область с сеткой конечных элементов в пакете «ELCUT»
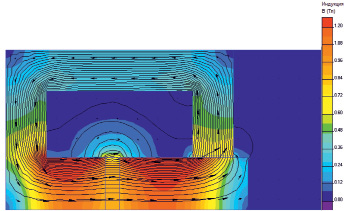
Рис. 3. Картина магнитного поля оптимальной геометрии электромагнитного двигателя на середине хода якоря хm = 5 мм. Полное число ампер витков Iw 3951 A
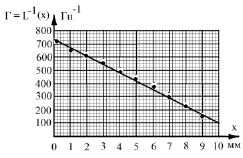
Рис. 4. Зависимость инверсной индуктивности катушки от хода якоря на основе расчета магнитного поля в пакете «ELCUT»
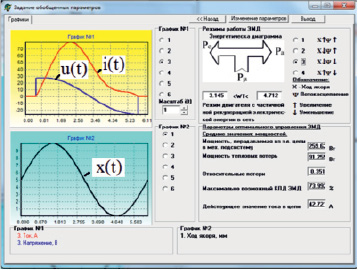
Рис. 5. Результаты исследований рабочего режима электромагнитного в главном окне программы «Анализ»
Для этой конструкции двигателя расчетом были найдены число витков катушки w = 85, активное сопротивление R = 0,045 Ом, среднее значение инверсной индуктивности на середине хода якоря a = 479,2 Гн–1, глубина модуляции инверсной индуктивности m = 0,41, добротность двигателя ρ = 0,0686, максимально возможный КПД электромагнитного двигателя ηmax = 62,5 %, масса двигателя mдв = 2,78 кг, масса медного провода mпр = 1,14 кг.
На поверочном этапе уточняются обобщенные параметры линейного электромагнитного двигателя с использованием численного расчета осесимметричной модели магнитного поля для различных фиксированных значений рабочего зазора (линейная магнитостатика) с помощью комплекса программ «ELCUT 6.0» (профессиональная версия). Результаты расчета приведены на рис. 3 и 4.
Задавая в модели линейного электромагнитного двигателя различные значения рабочего зазора в пределах хода якоря, можно по рассчитанным картинам магнитных полей с помощью «Мастера индуктивности» определить зависимость инверсной индуктивности катушки от хода якоря. На графике (рис. 4) расчетные значения инверсной индуктивности катушки показаны точками, между которыми проходит аппроксимирующая прямая.
По результатам расчета среднее значение инверсной индуктивности катушки на середине хода якоря a = 407 Гн–1, а глубина модуляции инверсной индуктивности оказывается существенно выше прежней m = 0,71. Ввод полученных значений в диалоговое окно программы «Анализ» (рис. 5) и последующий пуск программы позволяет более точно определить энергетические показатели работы электромагнитного привода колебательного движения, а также проанализировать с помощью энергетических диаграмм, происходящие в нем процессы энергопреобразования.
Выводы
1. Предложена методика оптимального проектирования электромагнитного привода колебательного движения на заданный во времени закон движения якоря, основанная на установлении взаимосвязи между обобщенными параметрами привода, обеспечивающая максимально возможный его КПД в установившемся режиме работы.
2. На стадии предварительных расчетов оптимальной конструкции электромагнитного двигателя использование упрощенной модели магнитного поля и ее расчет методом вероятных путей магнитного потока позволяет существенно сократить объем вычислений и затраты времени на проектирование. Однако, при выполнении поверочных расчетов для надежности полученных результатов необходимо выполнить численный расчет картин магнитного поля для различных фиксированных значений рабочего зазора с использованием комплекса программ «ELCUT 6.0» (профессиональная версия) с возможностью последующей корректировки значений обобщенных параметров электромагнитного двигателя и уточнения геометрии его магнитной системы и обмоточных данных.