В настоящее время актуальность изучения распространения электромагнитных волн в растительных покровах земной поверхности связана, в основном, с необходимостью адекватной интерпретации данных дистанционного зондирования. При решении таких задач основной интерес представляет как определение электродинамических характеристик растительности в широком диапазоне частот, так и изучение различных эффектов, возникающих при взаимодействии радиоизлучения с элементами растительности. К числу таких эффектов, возможно проявляющихся при распространении волн УКВ диапазона в лесах определенного типа, может быть отнесена локализация электромагнитного излучения. Изначально концепция данного эффекта была предложена Андерсоном [1] в середине прошлого века применительно к описанию диффузии электронов в кристаллических решетках в случайном потенциале. Начиная с 1980-х годов понятие «локализация» начинает использоваться для описания эффектов, сопровождающих распространение электромагнитных (классических) волн в случайных дискретных средах.
Явление локализации может быть охарактеризовано двумя уровнями. Первый – это слабая локализация или усиление обратного рассеяния, связанное с взаимной когерентностью волн, многократно рассеянных на одних и тех же элементах среды при распространении во взаимно противоположных направлениях. Второй – сильная локализация (далее локализация) – полное подавление распространения волн в сильно рассеивающей среде.
На сегодняшний день можно выделить два основных критерия наступления локализации:
1. Коэффициент прохождения волн через непоглощающую среду приобретает экспоненциально убывающий характер, описываемый законом T ≈ exp(–L/lloc), где L – линейная протяженность среды, lloc – локализационная длина, являющаяся параметром, определяющим степень локализации излучения.
2. Удовлетворение параметров среды критерию Иоффе – Регеля: k l ≤ 1, где k – волновое число, l – длина свободного пробега электромагнитной волны.
Последний параметр, в свою очередь, может быть определен из анализа формы конуса обратного когерентного рассеяния волн от случайной среды либо из анализа скорости убывания когерентной составляющей интенсивности излучения при прохождении через среду на основе строгого численного моделирования. Кроме того, возможно и приближенное аналитическое описание параметра l, которое в случае разреженной среды приобретает вид [2]:
l = 1/σ·n, (1)
где σ – поперечник рассеяния элементов среды, n – их концентрация (в двумерных задачах – количество элементов на единицу площади).
Целью данной работы является теоретическое изучение возможности проявления локализационных состояний при распространении волн в лесных средах.
Анализ методики
Поскольку строгое численное решение задачи описания распространения волн в лесу, а, следовательно, и определение коэффициента прохождения волн через растительность представляет определенные трудности, достижение поставленной цели целесообразно проводить на основе аналитической оценки длины свободного пробега волн в лесной среде и последующего анализа выполнения критерия Иоффе-Регеля для различных параметров лесной растительности.
Будем рассматривать взаимодействие излучения низкочастотной части УКВ диапазона с хвойными лесами, типичным для значительной части территории Республики Бурятия, характеризующимися отсутствием подлеска и низко расположенных ветвей. Поскольку основное влияние на параметры поля такой лес оказывает за счет эффектов рассеяния и поглощения излучения стволами деревьев, в первом приближении моделью такой растительности может служить двумерная система случайным образом расположенных в пространстве диэлектрических цилиндров.
Оценим работоспособность выражения (1) при определении длины свободного пробега волн в таких структурах. Для этого, прежде всего, проведем сравнительный анализ точности вычисления данного параметра строгим методом и в соответствии с формулой (1) для случайных сред, в которых возможно достаточно простое строгое численное определение параметров поля. Рассмотрим структуру, представляющую собой N круговых сильно рассеивающих цилиндров радиуса a, размещенных случайно и параллельно друг другу в однородной среде в пределах прямоугольной площадки с изменяющейся длиной L и шириной W= 90 см, со средней плотностью ρ= 0,5 см-2. Структура возбуждалась полем линейного электрического тока, ориентированного параллельно цилиндрам, таким образом, рассматривается случай Е поляризации волн (рис. 1). Численное моделирование проводилось на основе теории многократного рассеяния [3]. Методика расчетов применительно к задачам рассеяния волн на системах цилиндрических элементов подробно обсуждалась в [4].
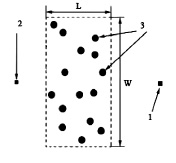
Рис. 1. Концептуальная схема рассматриваемой в работе системы: 1 – источник поля, 2 – место расположения приемника излучения, 3 – цилиндрические рассеиватели
Определялась относительная когерентная интенсивность излучения, прошедшего через рассматриваемую структуру:
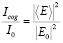 ,
,
где символ 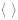 означает усреднение по 500 реализациям размещения элементов; I0, E0 – соответственно интенсивность и напряженность электрического поля в отсутствие структуры. Расчеты выполнялись для k = 0,5 см-1.
означает усреднение по 500 реализациям размещения элементов; I0, E0 – соответственно интенсивность и напряженность электрического поля в отсутствие структуры. Расчеты выполнялись для k = 0,5 см-1.
Длину свободного пробега волны для различных радиусов цилиндров в этом случае можно определить как расстояние, на котором относительная когерентная интенсивность Icog/I0 убывает в e раз, полагая Icog/I0 ≈ exp(-L/l). Из рис. 2 получаем l1 = 0,79 см при а = 0,05 см, l2 = 1,15 см при а = 0,01 см, l3 = 1,34 см при а = 0,005 см.
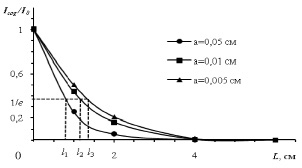
Рис. 2. Зависимость относительной когерентной интенсивности от протяженности структуры для различных радиусов цилиндров
Оценим теперь длину свободного пробега волны в рассмотренных случаях, используя выражение (1). Учитывая, что σ – поперечник рассеяния сильно рассеивающих (металлических) цилиндров кругового сечения – может быть определен как:
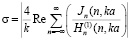 ,
,
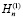 – функция Ханкеля первого рода n-го порядка, Jn – функция Бесселя m-го порядка; волновое число
– функция Ханкеля первого рода n-го порядка, Jn – функция Бесселя m-го порядка; волновое число
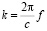 .
.
Получаем: l1* = 1,717 см при а = 0,05 см, l2* = 3,22 см при а = 0,01 см, l3* = 4,029 см при а = 0,005 см.
Таким образом, качественно полученные результаты определения длины свободного пробега волн двумя методами совпадают, при этом приближенный метод дает несколько большие оценки величины данного параметра. Отсюда следует, что для выявления локализации электромагнитных волн в лесной растительности возможно использование выражения (1).
Оценка возможности наблюдения локализации волн в лесу
Для определения рассеивающих свойств ствола дерева воспользуемся следующим выражением:
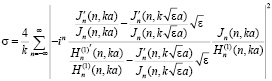 ,
,
описывающим поперечник рассеяния однородного диэлектрического цилиндра кругового сечения. Здесь символом ΄ обозначено дифференцирование по аргументу соответствующей цилиндрической функции, ε – модуль относительной диэлектрической проницаемости древесины ствола. Результаты измерений последнего параметра для различных видов деревьев представлены в работе [5], где, в частности, указывается, что для деревьев хвойных пород его значения лежат в диапазоне от 15 до 30.
Поскольку задача определения длины свободного пробега является многопараметрической, всесторонне исследование зависимости данной величины от частоты, поперечных размеров стволов, плотности древостоя и электрофизических параметров древесины было бы весьма громоздким. Поэтому рассмотрим только частные случаи, соответствующие характеристикам реального леса. При этом, наряду с определением длины свободного пробега волн в лесной среде, будем оценивать и локализационную длину lloc, характеризующую скорость убывания полной интенсивности излучения
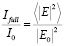
при прохождении через случайную среду. Расчет данного параметра вновь может проводиться с использованием строгих численных методов, при этом он определяется как дистанция, на которой полная интенсивность убывает в е раз. Кроме того, возможно и приближенное аналитическое описание данной величины, базирующееся на теории эффективной среды [6]:
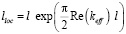 .
.
Здесь 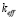 – эффективное волновое число, в свою очередь определяемое как
– эффективное волновое число, в свою очередь определяемое как
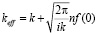 ,
,
где 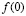 – функция рассеяния вперед отдельного элемента среды.
– функция рассеяния вперед отдельного элемента среды.
На рис. 3 и 4 представлены частотные зависимости параметра kl, соответствующего критерию Иоффе-Регеля, и локализационной длины lloc для модели леса, характеризующейся следующими параметрами: плотность древостоя – 0,2 м-2, диаметр стволов – 0,36 м, диэлектрическая проницаемость древесины ствола – 20.
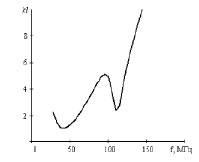
Рис. 3. Частотная зависимость параметра kl
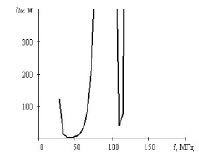
Рис. 4. Частотная зависимость параметра lloc
Выводы
Из полученных результатов следует, во-первых, возможность локализации излучения либо проявления близких к локализационным волновым состояниям в лесной среде. Если таковые будут иметь место, то окажут существенное влияние на параметры распространяющихся в данной среде электромагнитных волн. Во-вторых, представленные данные указывают на возможность локализационных проявлений только в низкочастотной части УКВ диапазона, причем в узких спектральных интервалах. Очевидно, это обусловлено резонансными свойствами одиночных диэлектрических цилиндров. Именно поэтому положение минимумов на представленных характеристиках оказывается весьма критичным к изменению параметров модели. Следовательно, выявление подобных эффектов при распространении волн в реальных лесных покровах возможно только при проведении экспериментов по широкополосному радиопросвечиванию лесной растительности.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант № 15-47-04315).

