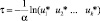Глобальный финансово-экономический кризис, ставший причиной системного сдвига в финансовой сфере мировой экономики продемонстрировал недостатки существующих методов, применяемых в области инвестиционной деятельности. Вопросам финансово-экономических методов инвестиционной деятельности посвящены исследования многих авторов. В них рассматриваются различные аспекты выбора инвестиционного проектов с учетом их различных показателей [1–7]. Анализ этих исследований показал, что основное внимание уделяется общим подходам к организации инвестиционной деятельности в рамках теории Г. Марковица, Тобина и др. Однако все возрастающий вес набирает проблема формирования и управления инвестиционной политики с позиции обеспечения эффективности принимаемых решений по выбору наиболее перспективных инвестиционных проектов в условиях различных непредсказуемых вызовов экономического, социального, экологического и другого характера.
Поэтому в данной статье разрабатывается конкретная процедура выбора инвестиционных проектов на основе теории принятия решений, хорошо зарекомендовавшая себя в организационных, социальных и других сферах человеческой деятельности.
Методы принятия решений в условиях неопределенности
Пусть имеется множество проектов, рассматриваемых в качестве претендентов на инвестирование
A = {Ai / i = 1, 2, …, n} (1)
характеризуемых показателями оценки их доходности Bi, i = 1, 2, …, n. Однако существует неопределенность, вызванная неполнотой или неточностью информации об условиях их реализации, например уровень инфляции. С учетом этой неопределенности экспертами оценены возможные варианты состояния S = {Sj / j = 1, 2, …, m} рынка товаров и услуг, относящихся к проектам из представленного множества (1). Такая информация может быть представлена в виде табл. 1.
Таблица 1
Значения экспертных оценок доходности проектов при различных ситуациях
|
Sj Ai |
S1 |
S2 |
… |
Sm |
|
A1 A2 . . An |
b11 b21 . . bn1 |
b12 b22 . . bn2 |
… … … … … |
b1m b2m . . bnm |
Здесь bij = f(Ai, Sj), i = 1, 2, …, n, j = 1, 2, …, m – доходность инвестиции в проект Ai при возможной инфляционной ситуации на рынке Sj.
При необходимости знания для определения bij = f (Ai, Sj) количественных значений каждого из вариантов состояния Sj, j = 1,2, …, m, задаются законы распределения их возможных значений, обычно в виде случайных дискретных величин
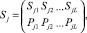 j = 1, 2, …, m.
j = 1, 2, …, m.
Для определения конкретных значений Sjl каждого из вариантов состояния Sj, j = 1, 2, …, m используется метод, основанный на теореме 1 «Величина Sjl наступает с вероятностью Pjl при выполнении условия u Î ∆l, где∆l = Pjl и u – равномерно распределена в интервале [0, 1]». Доказательство данной теоремы можно найти, например, в [10].
Для определения эффективной стратегии инвестирования воспользуемся известными критериями принятия решений в условиях неопределенности: Вальда, Лапласа, Гурвица и Сэвиджа [8]. По критерию Вальда, которую в данном случае можно назвать критерием осторожного инвестора, выбор проекта Ai* осуществляется в предположении, что рынок будет находиться в самом невыгодном для него состоянии. Аналитически это записывается выражением
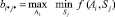 (2)
(2)
обеспечивающим наибольшее значение доходности из всех ее минимальных значений. Таким образом эффективным по критерию Вальдаявляется стратегия инвестирования в проект Ai*.
По критерию Гурвица предполагается, что рынок может находиться в самом невыгодном состоянии с вероятностью (1 – τ) и в самом выгодном – с вероятностью (τ), где τ – коэффициент доверия. Тогда правило выбора проекта для инвестирования примет вид
При τ = 0 из (3) получим выражение критерия Вальда. При τ = 1 приходим к стратегии инвестора – оптимиста:
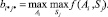
Величина коэффициента доверия сама является случайной величиной и в зависимости от вида рынка товаров и услуг может описываться различными законами распределения. Поэтому для определения ее значения можно воспользоваться методом обратной функции моделирования непрерывных случайных величин, принцип которого формулируется в виде теоремы 2 [9]: «Случайная величина τ, реализации которой определяются из выражения
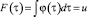 или τ = F–1(u),
или τ = F–1(u),
где u – равномерно распределена в интервале [0, 1], имеет заданную плотность распределения φ(τ)». Если функция плотности φ(τ) является непрерывной случайной величиной и подчиняется одному из известных стандартных теоретических законов распределения, то для моделирования значений τ можно воспользоваться формулами, приведенными в табл. 2 [10].
Критерий Лапласа используется при отсутствии информации о будущем состоянии рынка и тогда все состояния рынка считаются равновероятными. Этому критерию соответствует аналитическое выражение
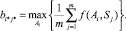 (4)
(4)
Наконец, критерий Сэвиджа используется для минимизации размеров максимальных потерь по каждому из принимаемых решений. При использовании данного критерия таблица 1 преобразуется в таблицу потерь (сожалений) в соответствии с формулой
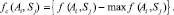 (5)
(5)
Тогда аналитическое выражение критерия Сэвиджа имеет вид
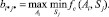 (6)
(6)
Алгоритм выбора проекта в условиях неопределенности
Построим алгоритм выбора единственного проекта из множества проектов (1) в условиях неопределенности
Шаг 1. Задание элементов табл. 1.
Шаг 2. Определение проекта Ai* оптимальной по критерию (2).
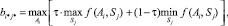 где τ ∈ [0, 1]. (3)
где τ ∈ [0, 1]. (3)
Таблица 2
Формулы моделирования основных теоретических распределений непрерывных случайных величин
|
Распределение |
Функция плотности |
Формула для моделирования |
|
Нормальное |
|
|
|
Равномерное |
|
|
|
Экспонентное |
|
|
|
Линейное |
|
|
|
Гамма |
|
|
Шаг 3. Определение проекта Ai* оптимальной по критерию (3).
Шаг 4. Определение проекта Ai* оптимальной по критерию (4).
Шаг 5. Составление таблицы потерь в соответствии с формулой (5).
Шаг 6. Определение проекта Ai* оптимальной по критерию (6).
Шаг 7. Вычисление для выбранных по каждому критерию оптимальных проектов одного из стандартных показателей их эффективности (индекс рентабельности, срок окупаемости и др.).
Шаг 8. Сравнительный анализ результатов, полученных по разным критериям по значениям дополнительного стандартного показателя.
При необходимости выбора нескольких (k) проектов для инвестирования алгоритм преобразуем к следующему виду.
Шаг 1. Задание элементов табл. 1.
Шаг 2. Выбор одного из критериев, реализуемых выражениями (2, 3, 4, 6).
Шаг 3.1. Определение проекта Ai* оптимальной по критерию (2).
Шаг 3.2. Определение проекта Ai* оптимальной по критерию (3).
Шаг 3.3. Определение проекта Ai* оптимальной по критерию (4).
Шаг 3.4.1 Составление таблицы потерь в соответствии с формулой (5).
Шаг 3.4.2 Определение проекта Ai* оптимальной по критерию (6).
Шаг 4. Исключение из табл. 1 строки, соответствующей выбранному проекту и переход к реализации шага 3*, выбранной ранее на шаге 2 до определения k проектов, подлежащих инвестированию.
По второму алгоритму для определения всех k проектов используется только один, выбранный на шаге 2 критерий. Однако при наличии дополнительных показателей проектов, не подверженных рыночным колебаниям, здесь также можно осуществить сравнительный анализ результатов, полученных по разным критериям.
Заключение
В последнее время растет интерес к процедурам анализа эффективности и выбора инвестиционной деятельности. Причиной стал мировой финансово-экономический кризис, отразивший недостатки применяемых в прошлом методов. В статье приведены методы принятия инвестиционных решений и разработан алгоритм выбора перспективного проекта в условиях неопределенности, которые в будущем будут использованы при разработке инструментального средства, позволяющего детально описать инвестиционную деятельность. Преимуществом представленных методов и алгоритма является возможность выбора наиболее эффективного варианта из альтернативных инвестиционных проектов в условиях неопределенности, учет неопределенности и рисков, связанных с осуществлением проекта.


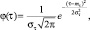 –∞ < τ < ∞
–∞ < τ < ∞
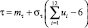
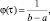 τ ∈ [a, b]
τ ∈ [a, b]
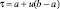
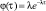 τ ≥ 0
τ ≥ 0
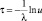
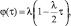
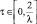
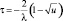
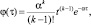 α > 0, k > 0, τ ≥ 0
α > 0, k > 0, τ ≥ 0