На сегодняшний день каналы передачи данных и носители информации остаются далекими от совершенства. Кабельные и беспроводные линии передачи информации подвержены воздействию внешних помех, искажающих форму передаваемых сигналов и тем самым делающих невозможным однозначное распознавание информации на стороне приемника, магнитные и оптические носители информации чувствительны к физическим повреждениям, делающим невозможным чтение информации из отдельных участков на поверхности носителя.
В настоящее время в системах хранения и передачи данных применяют различные технологии информационного резервирования с применением специальных алгоритмов кодирования на базе корректирующих кодов, в частности, кодов Рида-Соломона [1], которые за счет использования избыточной информации делают возможным исправление искажений. Однако, алгоритмы кодирования и декодирования информации с применением кодов Рида-Соломона достаточно нетривиальны, и для эффективной программной или аппаратной реализации требуется достаточно глубокая математическая проработка с применением алгебры конечных полей Галуа [2]. В частности, алгоритм декодирования состоит из блока вычисления синдрома искажений, полинома локаторов искажений, самих локаторов искажений и значений искажений, и все блоки имеют дело с полиномами, заданными над конечным полем Галуа. Особое место занимает блок вычисления значений искажений на базе метода Форни, использующего формальную производную полинома заданного над полем Галуа, и здесь требуется особый подход для построения эффективного алгоритма вычисления значения формальной производной полинома при заданном аргументе.
В рамках научных исследований автора в области надежности систем хранения, передачи и обработки данных [3–9], а также в области информационного резервирования [10] возникла научная задача разработки эффективного алгоритма вычисления формальной производной полинома Ψ(x), заданного над полем Галуа GF(pm), при заданном аргументе x, и аппаратной реализации для поля Галуа GF(2m).
Полином над полем Галуа. Пусть задано поле Галуа GF(pm). Тогда полиномом, заданным над полем Галуа, будем называть функцию:
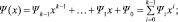
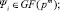
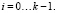(1)
Над полиномами можно производить алгебраические операции, также на место переменной x можно подставлять конкретное значение, являющееся элементом поля Галуа GF(pm), и вычислять значение функции. При пересчете коэффициентов полинома при выполнении операции или вычислении значении функции, строго соблюдаются правила арифметики для поля GF(pm).
Формальная производная полинома. Вычисление производной от полинома, заданного в поле Галуа, требует особого подхода, так как мы не можем говорить о бесконечно малых величинах, поскольку в поле Галуа нет таких элементов, которые бы мы могли использовать в качестве бесконечно малого. Однако, никто нам не запрещает говорить о некоторой формальной бесконечно малой величине, обозначим ее ε, которая будет нами использоваться исключительно для выполнения математических преобразований.
Кроме того, ради общности рассуждений мы рассмотрим формальную производную полинома, заданного над полем Галуа GF(pm), а затем рассмотрим частный случай производной над полем Галуа GF(2m).
Тогда, мы можем дать определение формальной производной функции f(x):
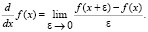(2)
Особо отметим, что не следует «в лоб» пытаться искать численное значение предела при конкретных значениях аргумента x. Формула задана исключительно для аналитических преобразований, подразумевающих исключение величины ε из итогового аналитического выражения для производной функции. Заметим, что так же, как и в традиционной алгебре, здесь справедливы следующие свойства формальной производной функции:
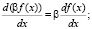
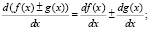
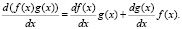
Теперь же выведем формальные производные для простейших функций:
● Константная функция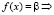 
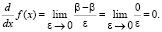
● Функция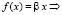 
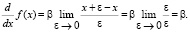
Однако, прежде чем продолжить выводить производные степенных функций более высокого порядка, рассмотрим подробнее выражение (x + ε)k, k ≥ 1. В традиционной алгебре для возведения в степень k выражения x + ε существует простая общая формула:
.
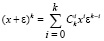Биномиальный коэффициент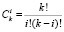 
представляет собою количество одинаковых (повторяющихся) слагаемых xiεk–i (для каждого i = 0…k), образуемых и затем складывающихся при возведении в степень k выражения 
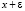. Учтем арифметическое свойство полей Галуа GF(pm):
,
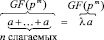где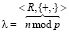 
.
В нашем случае, a = xiεk–i и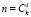 
, и тогда:
.
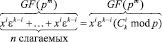Тогда, учитывая все сказанное, можно вывести общую формулу для (x + ε)k, k ≥ 1:
.
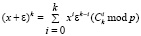Теперь, наконец, вычислим производную от функции
.
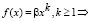
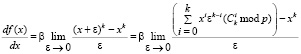Выделим из суммирования слагаемое xk при i = k, и учтем, что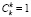 
и ε0 = 1. Тогда в итоге имеем:
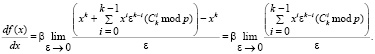
Заметим, что в числителе среди оставшихся слагаемых суммирования, только при i = k – 1, слагаемое xk–1ε содержит ε в первой степени, которое может сократиться с ε в знаменателе, а при i ≤ k – 2, слагаемые содержат ε в степени большей, чем 1, и оно не уничтожится вместе с ε в знаменателе, и после взятия предела слагаемые превратятся в нуль, поскольку будут содержать ε в ненулевой степени.
Тогда,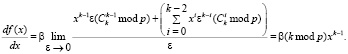 
Таким образом, окончательно: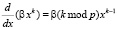 
при k ≥ 1.
Теперь мы можем, вывести формулу для вычисления формальной производной от полинома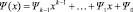 
, заданного над полем Галуа GF(pm):
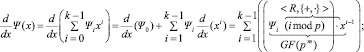
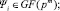
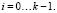(3)
Особо отметим, что выражение Ψi(imodp) вычисляется как произведение элементов Ψi и λ в поле GF(pm), где элемент λ численно равен imodp в традиционной арифметике действительных чисел, но интерпретируется именно как элемент поля GF(pm).
В частном случае, если мы вычисляем формальную производную от полинома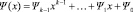 
, заданного над полем Галуа GF(2m), мы имеем формулу:
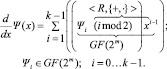(4)
Заметим, что выражение (imod2) приводит к тому, что в полях GF(2m), коэффициенты Ψi с четными индексами, стоящие при переменной xi-1 у полинома-производной, умножаются на нуль, и, соответственно, в полиноме-производной всегда отсутствуют слагаемые с нечетными степенями переменной x.
Пример. Формальная производная Ψ(x) = 100x4 + 218x3 + 31x2 + 3x + 51, заданного над полем GF(28):
.
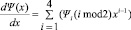
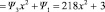Вычисление значения формальной производной полинома при заданном аргументе над полем Галуа GF(2m). Выше мы выяснили, что формальная производная полинома Ψ(x) над полем GF(2m) определяется как:
.
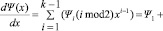
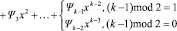Теперь формальную производную полинома можно переписать в следующем виде:
.
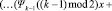
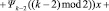
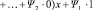После этого мы можем применить следующую рекуррентную схему вычисления значения формальной производной полинома Ψ(x) при заданном аргументе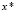 
:
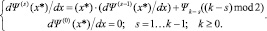(5)
После k – 1 итераций, результат вычислений на последней итерации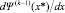 
и будет являться искомым значением формальной производной dΨ(x)/dx при заданном аргументе x*. Заметим, что если k = 0 или k = 1, то в качестве результата возвращается нуль, а если k = 2 или k = 3, то в качестве результата возвращается Ψ1.
Пример. Вычислим значение формальной производной полинома Ψ(x) = 222x5 + 29x4 + 34x3 + 183x2 + 232x + 1 заданного над полем GF(28) при x = 64.
С одной стороны, формальная производная полинома имеет следующий вид: dΨ(x)/dx = 222x4 + 34x2 + 232 . Подставляя в нее x = 64, получаем значение формальной производной 222∙644 + 34∙642 + 232 = 70.
С другой стороны, можно получить тот же результат, не прибегая к расчету полинома-производной dΨ(x)/dx, используя лишь только исходный полином Ψ(x) и применив к нему рекуррентную схему вычисления значения формальной производной: ((((222∙1)∙64 + 29∙0)∙64 + 34∙1)∙64 + + 183∙0) ∙64+ 232∙1 = 70.
Аппаратная реализация для поля Галуа GF(2m). Теперь рассмотрим аппаратную реализацию вычисления значения формальной производной dΨ(x)/dx при заданном аргументе x* над полем Галуа GF(2m). Ниже на рисунке приведена предлагаемая автором функциональная схема последовательного вычислителя dΨ(x*)/dx.
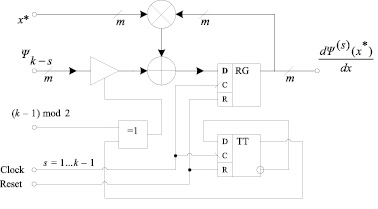
Функциональная схема аппаратной реализации последовательного вычислителя значения формальной производной dΨ(x)/dx при заданном аргументе x*
Схема содержит, счетный D-триггер (TT), который перед началом вычислений сбрасывается, а затем с приходом каждого тактового сигнала меняет свое состояние на противоположное состояние. Выход триггера подключен к логическому элементу XOR, ко второму входу которого подается 1, если степень полинома Ψ(x) является нечетной, или 0, если степень является четной. В итоге на управляющий вход коммутационной схемы 
, поступает последовательность 101…101 при нечетной степени полинома Ψ(x), и 01…101 при четной степени полинома. Таким образом, коммутационная схема всегда блокирует коэффициенты с четными индексами, коэффициенты с нечетными индексами, наоборот, всегда пропускает.
Также схема содержит m-разрядный регистр (RG) для хранения текущего результата вычислений. Кроме того, схема содержит m-разрядный сумматор 
элементов Галуа GF(2m), который реализуется при помощи m двухвходовых логических элементов XOR. Наконец, схема также содержит m-разрядный умножитель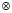 
элементов Галуа GF(2m), который также может быть реализован при помощи m2 двухвходовых элементов «И» и m многовходовых сумматоров по модулю 2. Аппаратная реализация быстрых сумматоров и умножителей элементов поля Галуа GF(2m) хорошо освещены в литературе [1, 2].
Изначально схема сбрасывается сигналом, подаваемым на вход Reset, тем самым и регистр и триггер сбрасываются в нулевое значение. При поступлении очередного тактового сигнала s = 1…k – 1 на один вход сумматора поступает результат умножения содержимого регистра на аргумент x*, а на второй вход сумматора поступает очередной коэффициент Ψk–s, если k – s является нечетным, и он складывается с результатом умножения, и сумма записывается в регистр, если же k – s является четным, то на второй вход сумматора поступает нуль, и в итоге в регистр записывается результат умножения без изменений. В итоге после k – 1 тактов на выходе регистра мы получаем искомое значение формальной производной dΨ(x*)/dx при заданном аргументе x*.
Следует особо отметить, что регистр (RG) записывает информацию со своих входов по фронту тактовых импульсов, а триггер (TT) переключается по спаду тактовых импульсов. Такой двухтактный подход позволяет избегать переключения коммутационной схемы в момент записи информации в регистр.
Заключение
Таким образом, в рамках данной статьи рассматривается алгоритм вычисления формальной производной полинома над полем Галуа. В статье приведено определение полинома, формальной производной полинома и формула для ее вычисления над полем Галуа GF(pm).
Также в статье рассматривается алгоритм вычисления значения формальной производной полинома над полем Галуа GF(2m) при заданном аргументе и предлагаемая автором аппаратная реализация алгоритма.
Полученные результаты были использованы автором для разработки обучающей программы и лабораторных стендов для изучения студентами технических специальностей технологии кодирования информации при применении кодов Рида-Соломона.