Развитие сверхкритических технологий требует новых методов диагностики сверхкритических и околокритических флюидов, а также новых подходов к системам управления процессами в различного вида устройствах, использующих сверхкритические и околокритические флюиды в качестве рабочего тела. В последнее время широкое распространение получила акустическая диагностика околокритических сред, с помощью которой может быть получена информация о положении границы раздела фаз, скорости звука и термодинамических параметрах. Ведутся работы по созданию управляемого во времени и пространстве теплового поля внутри СКФ за счет поглощения лазерного излучения. Использование этого метода позволит создавать нагретые области заданной конфигурации и осуществлять тонкое регулирование интенсивности подвода тепла по заданному закону [1].
Численные и экспериментальные исследования теплопереноса в замкнутом объеме, наполненном сверхкритическим флюидом (СКФ), особенно интенсивно развивались в последние два десятилетия, в частности благодаря международным экспериментам, проведенным на борту орбитальных станций МИР и МКС. Было обнаружено, что при нагреве или охлаждении границ объема с СКФ наблюдается существенное ускорение прогрева/охлаждения объема среды при приближении к критической термодинамической точке [7, 8]. Другой замечательной особенностью теплопереноса в СКФ при приближении к критической точке является существенное замедление релаксации неоднородностей термодинамических полей, вызванных, например, подводом тепла [9].
При объемном и/или поверхностном подводе тепла в сверхкритическом флюиде образуются волны давления, температуры, плотности и скорости [10]. Поэтому для понимания причин возникновения упомянутых выше особенностей важно проследить за распространением таких возмущений в максимально простой постановке.
Примером такой постановки является задача о распаде произвольного разрыва температуры и давления. Такой разрыв возникает, например, при динамическом лазерном нагреве, вследствие которого в начальный момент времени разные части неподвижного объема среды приобретают разные температуру и давление, но имеют одинаковую плотность.
В работе исследуется распад слабого разрыва температуры и давления методом возмущений уравнений Навье-Стокса.
Математическая модель
Безразмерная система уравнений состояния, баланса энергии, движения и неразрывности имеет вид:
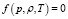 , (1)
, (1)
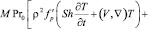
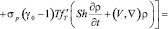
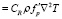 , (2)
, (2)
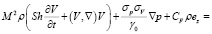
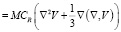 , (3)
, (3)
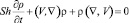 . (4)
. (4)
Здесь введены следующие безразмерные комплексы (курсивом обозначены размерные величины):
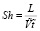 – число Струхала, L – масштаб длины,
– число Струхала, L – масштаб длины, 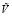 – масштаб скорости и
– масштаб скорости и 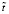 – масштаб времени.
– масштаб времени.
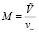 – число Маха,
– число Маха,
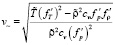 – скорость звука при масштабных термодинамических параметрах
– скорость звука при масштабных термодинамических параметрах 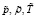 , где
, где 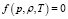 .
.
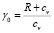 – показатель адиабаты или адиабатическая постоянная.
– показатель адиабаты или адиабатическая постоянная.
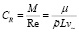 ,
, 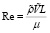 – число Рейнольдса. Параметр CR позволяет сопоставить влияние трения при скоростях диффузионных процессов с влиянием трения, возникающего при движении со звуковыми скоростями в среде с масштабной плотностью в масштабном объеме.
– число Рейнольдса. Параметр CR позволяет сопоставить влияние трения при скоростях диффузионных процессов с влиянием трения, возникающего при движении со звуковыми скоростями в среде с масштабной плотностью в масштабном объеме.
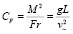 ,
, 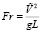 – число Фруда. Параметр CF соотносит потенциальную энергию пробной массы при заданном тяготении на уровне масштабной высоты с кинетической энергией, которую приобретает эта масса, двигаясь со скоростью звука.
– число Фруда. Параметр CF соотносит потенциальную энергию пробной массы при заданном тяготении на уровне масштабной высоты с кинетической энергией, которую приобретает эта масса, двигаясь со скоростью звука.
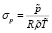 – коэффициент, характеризующий уклонение выбранного масштаба давления от давления совершенного газа при выбранных масштабах плотности и температуры.
– коэффициент, характеризующий уклонение выбранного масштаба давления от давления совершенного газа при выбранных масштабах плотности и температуры.
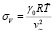 – коэффициент, характеризующий уклонение квадрата скорости звука в совершенном газе при выбранном масштабе температуры от квадрата скорости звука исследуемого газа при масштабных термодинамических параметрах.
– коэффициент, характеризующий уклонение квадрата скорости звука в совершенном газе при выбранном масштабе температуры от квадрата скорости звука исследуемого газа при масштабных термодинамических параметрах.
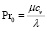 – число Прандтля. Формально
– число Прандтля. Формально 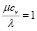 , однако, на практике параметр Pr0 указывает отклонение этого отношения от единицы.
, однако, на практике параметр Pr0 указывает отклонение этого отношения от единицы.
Отметим, что система уравнений (1)-(4), в области надкритичности, определяемой условиями надкритичности
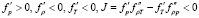 ,
,
(см. [2] (3.5)) согласно предположениям, описывает движение газа с постоянными физическими свойствами при постоянной гравитации для произвольного уравнения состояния в параллелепипеде П с безразмерными сторонами Lx, Ly, Lz, именно,
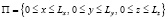 . (5)
. (5)
Безразмерная скорость звука определяется формулой:
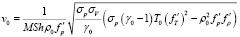 . (6)
. (6)
Для совершенного газа 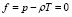 , для газа Ван-дер-Ваальса
, для газа Ван-дер-Ваальса
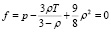 .
.
Из системы уравнений (1)-(4) при соблюдении условий надкритичности можно получить систему уравнений, определяющую механическое равновесие системы, линеаризованное механическое равновесие (квазиравновесие), а затем возмущенную систему уравнений динамики газа:
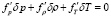 , (7)
, (7)
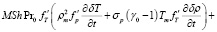
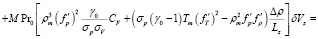
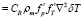 , (8)
, (8)
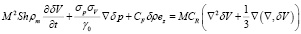 , (9)
, (9)
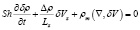 , (10)
, (10)
где функции 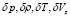 являются малыми возмущениями квазиравновесия.
являются малыми возмущениями квазиравновесия.
Эта система состоит из возмущенных уравнений состояния, баланса энергии, движения и неразрывности. Из возмущенных уравнений баланса энергии и движения следует, что в зависимости от соотношения порядков величин CR, CF, Δρ (Δρ– перепад плотности) различаются следующие случаи (см. также [3]):
1. Однородная среда в невесомости:
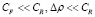 . (11)
. (11)
2. Стратифицированная среда в невесомости:
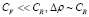 . (12)
. (12)
3. Среда однородной плотности в гравитационном поле:
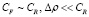 . (13)
. (13)
4. Стратифицированная среда в гравитационном поле:
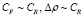 . (14)
. (14)
Согласно формулам (7)-(10) (см., также работу [4]) динамика возмущений механического равновесия однородной среды в невесомости при одномерной постановке, где параллелепипед (5) является отрезком [0, Lz], определяется системой уравнений:
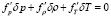 , (15)
, (15)
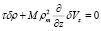 , (16)
, (16)
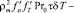
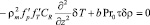 . (17)
. (17)
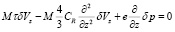 , (18)
, (18)
Здесь для удобства введены обозначения:
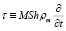 ,
, 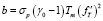 ,
,
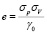 . (19)
. (19)
Система уравнений (15)-(18) может быть сведена к уравнению (см. [5])
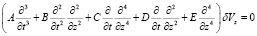 , (20)
, (20)
где
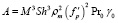 ,
,
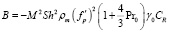 ,
,
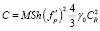 ,
,
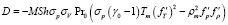 ,
,
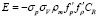 .
.
Отметим, что при условиях надкритичности для коэффициентов приведенного уравнения (20) имеют место оценки:
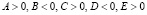 . (21)
. (21)
Для граничных условий непротекания применение метода разделения переменных [6] обеспечивает полную систему собственных функций уравнения (20), что позволяет при граничных условиях теплоизоляции концов отрезка [0, Lz] построить полную систему собственных функций системы уравнений (15)-(19). Таким образом, разложение в ряды Фурье по собственным функциям системы (15)-(19) произвольных начальных условий, в частности упомянутых выше разрывов температуры и давления, дает возможность изучать эволюцию во времени скорости и термодинамических параметров. В расчетах количество собственных функций принималось равным 1000.
Для вычисления безразмерных комплексов, входящих в уравнения (1)-(4) использовались следующие константы (для SF6): cv = 1000 дж/кг×град, λ = 1,2 вт/м×град, μ = 40×10-6 Па×с, R = 56,9 дж/кг×град, γ0 = 1,0569, и масштабы переменных: L = 10-2 m, 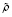 = ρc = 744 кг/м3,
= ρc = 744 кг/м3, 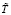 = Тс = 45,7 °С,
= Тс = 45,7 °С, 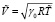 = 134,8 м/c,
= 134,8 м/c, 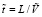 = 7,4×10-5 c.
= 7,4×10-5 c.
Далее рассматриваются два примера применения метода: распад слабого разрыва давления и температуры в центре и вблизи границ расчетной области, представляющей собой отрезок [0, 1] оси х.
Результаты расчетов
Распад слабого разрыва температуры и давления в центре расчетной области. Этот пример иллюстрирует особенности поведения возмущений термодинамических параметров и скорости при приближении к критической точке на больших временах (значительно превосходящих акустическое 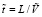 ).
).
Начальный разрыв температуры и давления располагается в центре (х = 0,5) расчетной области. При 0 < x < 0,5 среда имеет температуру Т1, а при 0,5 < x < 1 – температуру Т2. На основе метода малых возмущений были выполнены расчеты распада разрыва и последующей релаксации термодинамических параметров и скорости в одномерном случае для различных значений удаленности начальной температуры от критического значения [2]. После начала распада разрыва температура (давление) в правой половине области начинает расти, достигает максимума, затем падает и достигает минимума. Соответственно в левой половине температура (давление) падает, достигает минимума, затем растет и достигает максимума. В силу принятой нормировки времени полный цикл происходит за две единицы безразмерного времени (t = 2). При отсутствии вязкости и теплопроводности колебания будут происходить бесконечно долго, а форма начального распределения параметров меняться не будет. В нашем случае начальный разрыв температуры с течением времени деформируется вследствие действия теплопроводности и вязкости. На рис. 1 представлены распределения температуры, относящиеся к различным моментам безразмерного времени t = 0, 10, 100, 1000, и 10000 при начальной разнице Т1–Т2 = 10-6.
Степень релаксации можно характеризовать величиной максимума производной распределения температуры по пространству в середине расчетной области (х = 0,5). Её начальное значение максимально, а конечное должно стремиться к нулю.
Из рис. 2 видно, что при приближении к критической точке (уменьшении T2-Tc) скорость релаксации падает.
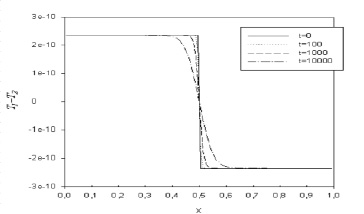
Рис. 1. Релаксация начального возмущения температуры T1-T2 при Т2-Тс = 450 мК
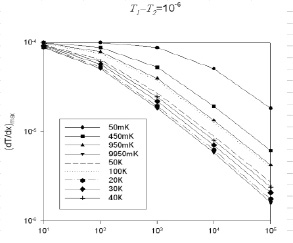
Рис. 2. Зависимость максимума производной распределения возмущения температуры по пространству от времени для различных значений разности начальной и критической температуры (Т2-Тс = 50 мК, 450 мК, 950 мК, 9950 мК, 20 К, 30 К, 40 К, 50 К, и 100 К)
Начальная стадия распада слабого разрыва температуры и давления вблизи границ расчетной области. Этот пример иллюстрирует особенности нагрева толщи среды при приближении к критической точке на временах порядка акустического времени.
Предполагается, что в начальный момент существует две поверхности разрыва: на расстоянии 0,1 от левой и правой границ области. Перепад температуры равен T1-T2 = 10 мК, а начальная температура Т2 = Тс + 450 мК. С течением времени наблюдается формирование импульсов, двигающихся навстречу друг другу со звуковой скоростью, их столкновение, обратное движение к границам и отражение от границ.
Предметом исследования является поведение термодинамических параметров и скорости в центре расчетной области (х = 0,5). Форма распределений и величина генерируемых импульсов температуры, плотности, скорости и давления существенно зависят от близости критической точки и различны для газа Ван-дер-Ваальса и совершенного газа.
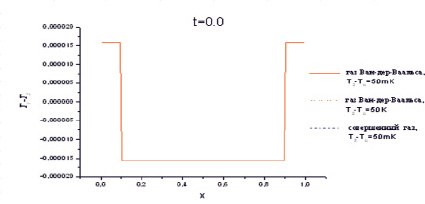
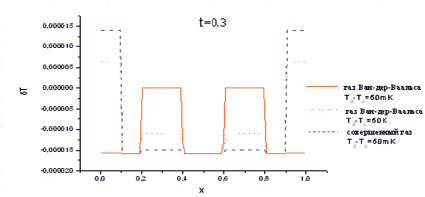
На рис. 3 представлены распределения температуры в начальный момент времени (рис. 3, а) и в момент времени t = 0,3 (рис. 3, б) для газа Ван-дер-Ваальса при Т2-Тс = 50 мК и 50 К.
а)
б)
Рис. 3. Распределения возмущений температуры в расчетной области (а) в начальный момент времени и (б) в момент времени t = 0,3 для газа Ван-дер-Ваальса (vdW) при Т2-Тс = 50 мК и 50 К и для совершенного газа (perf.). Начальное распределение температуры одинаково для всех трех случаев
Здесь же приведены распределения температуры для совершенного газа, которые практически не зависят от выбранных начальных температур. Из рисунка видно, что вблизи критической точки (50 мК) формируется значительно больший импульс, чем на существенном от неё удалении (50 К). При этом в совершенном газе сформировавшийся импульс температуры еще меньше, чем на значительном удалении от критической точки для газа Ван-дер-Ваальса. Стоит отметить, что вдали от критической точки характер распределения и высота импульсов температуры приближается к их значениям для совершенного газа.
Рассчитанные временные распределения температуры использовались для нахождения аналогичной зависимости для средней температуры в центре исследуемой области. На рис 4 представлена зависимость от времени среднего значения возмущений температуры для случая газа Ван-дер-Ваальса и совершенного газа. В случае газа Ван-дер-Ваальса наблюдается быстрый рост, а затем довольно быстрый спад температуры. В совершенном газе в этот период времени происходит относительно медленный подъем температуры. На больших временах температура в том и другом случае стремится к конечной (средней по объему) величине.
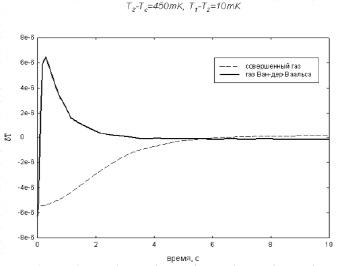
Рис. 4. Зависимость среднего значения возмущения температуры в центре расчетной области от времени (в секундах) для газа Ван-дер-Ваальса (сплошная линия) и совершенного газа (пунктирная линия)
Заключение
На основе точных решений линеаризованной системы уравнений Навье-Стокса, полученной методом возмущений механического равновесия, проведено исследование особенностей процесса распространения возмущений температуры, плотности, скорости и давления в замкнутом объеме среды вблизи термодинамической критической точки. В качестве уравнения состояния использовались уравнения состояния совершенного газа и газа Ван-дер-Ваальса. Полученное решение показало, что при приближении к критической точке происходит аномальное ускорение прогрева толщи среды и замедление темпа релаксации волн.
Предложенный метод возмущений механического равновесия уравнений Навье-Стокса может быть применен для исследований особенностей распространения возмущений термодинамических параметров, вызванных лазерно-индуцированным нагревом сверхкритического флюида, и имеет несомненные преимущества перед прямым численным расчетом на больших временах с точки зрения экономии машинного времени.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант № 15-01-02012).

