В классической механике динамика материальной точки описывается дифференциальными уравнениями для ее радиус-вектора, использующими обычную производную второго порядка по времени. Именно ее использование обеспечивает Галилей-инвариантность уравнений. Если соединить множество массивных материальных точек невесомыми упругими нитями в единую струну, то ее колебание будет описываться Галилей-инвариантной системой дифференциальных уравнений. Но если совершить предельный переход, устремив число материальных точек к бесконечности, а их массы и длины отдельных нитей – к нулю, то мы получим одномерное волновое уравнение (уравнение колебаний струны), не инвариантное относительно преобразований Галилея, но зато инвариантное относительно группы псевдоортогональных преобразований (гиперболических поворотов, сохраняющих псевдоевклидову метрику). Виновник такой странной и неожиданной метаморфозы при переходе от «материально-точечной механики к сплошной среде – этот предельный переход с подменой обычной производной на частную, который, вообще говоря, аналитически законен [1], но сужает область физической применимости уравнения. Реальный волновой процесс механических колебаний струны остается Галилей-инвариантным, но его уравнение уже лишено математических средств описания перехода от одной инерциальной системы отсчета к другой, а всецело привязывает процесс к одной конкретной системе отсчета, закрепляя в ней концы струны. Так классико-полевая естественнонаучная парадигма вскрыла фундаментальное противоречие между непрерывностью и дискретностью [5-6], не преодоленное до сих пор, но приведшее к торжеству в теоретической физике сомнительного принципа геометризации [7].
Открытие волнового уравнения в механике не привело к пересмотру представлений о пространстве и времени, но к этому привело открытие того же самого уравнения в электродинамике. В теории относительности соответствующая группа псевдоортогональных преобразований для электромагнитных волн в вакууме (преобразования Лоренца) получила статус подгруппы движения метрики единого мирового физического пространства-времени. Но возникает сомнение в оправданности использования традиционных уравнений электродинамики, в частности, волнового уравнения, для адекватного извлечения из них представлений о пространстве и времени. Легко предположить, что эти уравнения, используя частные производные полевых функций по времени, подобно уравнению механических колебаний, попросту лишены математических средств адекватного описания перехода от одной инерциальной системы отсчета к другой и так же всецело привязывают процесс к одной конкретной системе отсчета. Так возникает вопрос возможности подходящего уточнения или обобщения уравнений электродинамики, начиная с уравнений индукции электрического поля магнитным и магнитного – электрическим. Обстоятельное рассмотрение данного вопроса в [8] привело к появлению идеи о том, что такое совершенствование электродинамики должно предполагать существование зависимости электромагнитного поля от скорости движения наблюдателя, обусловленной не геометрией пространства-времени, а физической природой поля.
В теории относительности электромагнитное поле тоже зависит от скорости движения наблюдателя, но только опосредованно через зависимость от нее интервалов времени и пространственных расстояний (преобразования Лоренца), следствием чего оказывается релятивистская инвариантность электрического заряда. Более фундаментальная же (непосредственная) зависимость поля от скорости сопряжена с наличием такой зависимости даже абсолютной величины электрического заряда. До последнего времени такая не инвариантность заряда подтверждалась лишь косвенными эмпирическими данными, заключавшимися в появлении электрического потенциала на сверхпроводящих обмотках и торах при введении в них постоянного тока, а также в наблюдении электрического импульса ядерных взрывов. В частности, 9 июля 1962 года при взрыве в космосе над Тихим океаном водородной бомбы с тротиловым эквивалентом 1,4 Мт по программе США «Starfish» напряженность электрических полей превзошла предсказанные нобелевским лауреатом Бете Х.А. в 1000 раз. Однако 2015 год ознаменовался уже прямым экспериментальным подтверждением этого феномена в результате обнаружения и исследования импульса электрического поля, возникающего при разогреве плазмы в результате разряда через разрядники конденсаторов большой ёмкости [10]. Оказалось, что в процессе разогрева плазмы при равном количестве в ней электронов и положительных ионов в ней образуется унитарный отрицательный заряд свободных электронов, не скомпенсированный более медленными положительными ионами. Этот факт противоречит не только классическим, но и релятивистским преобразованиям электромагнитного поля при переходе от одной инерциальной системы отсчета к другой, свидетельствуя о несовершенстве не только классических, но и релятивистских представлений о пространстве.
Однако последовательное развитие такой радикальной идеи, как не инвариантность заряда, требует глубокого пересмотра математического аппарата электродинамики, призванного к созданию математических средств более адекватного описания перехода от одной инерциальной системы отсчета к другой. Естественно ожидать, что это должно привести к очередному пересмотру представлений о пространстве и времени с отказом от релятивистских и переходом к новым представлениям, которые мы называем гиперконтинуальными.
Понятие пространственно-временного гиперконтинуума введено в [3] в результате совместного изучения алгебраической и геометрической структур коммутативных алгебр с единицей, элементами которых являются функции синусоидальных волн. Гипотеза гиперконтинуума (об иерархической гиперконтинуальной структуре мирового физического пространства-времени) является отправной точкой научных исследований, направленных на обобщение представлений о структуре пространства и времени в русле перехода от современной квантовой научной парадигмы к новой системной, одновременно конструктивно соединяющей в своих рамках непрерывность и дискретность, динамичность и статичность, а также глобальность и локальность [5-6]. Иерархичность гиперконтинуума ограничивает применимость общепринятого принципа геометризации в физике и связанных с ним идей симметрии в геометрии за счет введения в теоретическую физику идей иерархичности [7], эффективность которых апробирована нами при создании эталонной модели защищенной автоматизированной системы (ЭМЗАС) и математического аппарата ЭМЗАС-сетей [4].
Цель исследования
Цель исследования – предложить новый подход к развитию математического аппарата электродинамики в направлении более адекватного описания перехода от одной инерциальной системы отсчета к другой на основе гиперконтинуальных представлений о пространстве и времени за счет совершенствования дифференциального исчисления полевых функций в предположении их зависимости от скорости движения наблюдателя.
Материалы и методы исследования
Рассмотрим две инерциальные системы отсчета с единым для них временем t∈ℝ. Одну из них (с системой прямоугольных декартовых пространственных координат OXYZ) назовем лабораторной (не штрихованной) и будем интерпретировать ее, как относительно неподвижную. Вторую (с системой прямоугольных декартовых пространственных координат O’X’Y’Z’) назовем субстанциональной (штрихованной) и будем интерпретировать ее, как связанную с некой движущейся реальной или воображаемой средой. Примем, что при t = 0 системы пространственных координат обеих систем отсчета совпадают. Координаты по осям OX, OY, OZ, O’X’, O’Y’, O’Z’ будем задавать переменными x1, x2, x2, x’1, x’2, x’3 соответственно. Через v = (vα) обозначим вектор скорости движения субстанциональной системы отсчета относительно лабораторной. Событие в данных двух системах отсчета имеет вид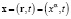 
, 
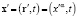, где r, r’ – радиус-векторы. Будем считать, что физическая эквивалентность событий x и x’ означает справедливость преобразования Галилея
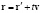. (1)
Классическое физическое поле описывается в лабораторной и субстанциональной системах отсчета своими полевыми функциями Ф(r, t) и Ф’(v, r’, t), причем Ф’(0, r’, t) = Ф’(r’, t), а равенство v = 0 означает vα = 0. Их значения называют полевыми переменными. Для полей разной физической природы могут подходить разные математические представления полевых функций, так что полевые переменные могут быть, например, скалярными или векторными с вещественными или комплексными значениями самих переменных или их векторных компонент. Если в роли такого поля выступает электрическое поле, то в данной роли могут выступать функции его напряженности E = Ф(r, t), E’ = Ф’(v, r’, t), а в случае магнитного поля имеем функции магнитной индукции B = Ф(r, t), B’ = Ф’(v, r’, t).
В классической нерелятивистской теории поля считается, что имеет место равенство:
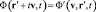, (2)
математически выражающее физическую концепцию инвариантности поля относительно скорости движения наблюдателя. В теории относительности (2) уже не выполняется, а вместо преобразований Галилея используются преобразования Лоренца. Но эта не инвариантность поля не имеет фундаментальной, не связанной с геометрией пространства-времени физической природы, а оказывается просто следствием эффектов сокращения длин и замедления времени в движущихся системах отсчета. Развиваемые нами гиперконтинуальные представления о пространстве и времени [3] предусматривают широкие возможности инвариантности тех или иных физических процессов относительно тех или иных групп преобразований координат при том, что особую роль в пространственно-временном гиперконтинууме играют преобразования Галилея (1), так как они при этом трактуются, как уровневые преобразования Лоренца бесконечно высокого уровня и, тем самым, позволяют единым образом синхронизировать все события во всех отдельных континуумах, иерархически структурирующихся в единый гиперконтинуум. Естественно считать, что в гиперконтинууме поле также не инвариантно относительно скорости движения наблюдателя, но объяснять это уже фундаментальными причинами, не связанными с геометрией отдельных континуумов.
Возникает вопрос о возможных вариантах полного дифференцирования по времени полевой функции в лабораторной системе отсчета Ф(r, t), производимого в зависимости от субстанциональной системы отсчета. В гидроаэромеханике и классической механике широко используется производная Лагранжа (субстанциональная производная), имеющая те же аргументы, что и исходная полевая функция:
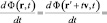
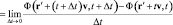. (3)
Но можно рассматривать также производную (назовем ее производной Галилея), аргументы которой будут совпадать с аргументами полевой функции уже не в лабораторной, а в субстанциональной системе отсчета:
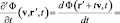
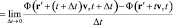. (4)
Если аргументы производных Лагранжа и Галилея связаны равенством (1), то их соответствующие значения равны и разлагаются в одну и ту же сумму частной по времени и конвективной производных полевой функции в лабораторной системе отсчета:
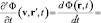
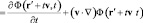. (5)
Поясним различие физического смысла лагранжевой и галилеевой производных полевой функции. Производная Лагранжа (3) есть полная производная по времени функции поля в лабораторной системе отсчета, измеряемого в точке пространства, которая в лабораторной системе отсчета в момент времени t имеет радиус-вектор r, определяемый равенством (1). А производная Галилея (4) есть полная производная по времени функции поля в лабораторной системе отсчета, измеряемого в точке пространства, которая в субстанциональной системе отсчета имеет радиус-вектор r’. Понятия лагранжевой и галилеевой производных (3)-(5) естественным образом обобщаются на случай производных высших порядков (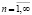
):
;
;
;
.
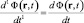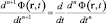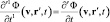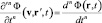В рамках концепции инвариантности поля относительно скорости движения наблюдателя, то есть при условии выполнения (2), имеем:
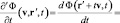
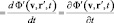, (6)
то есть галилеева производная функции поля в лабораторной системе отсчета неотличима от частной производной по времени функции поля в субстанциональной системе отсчета. Поэтому введение в рамках этой концепции производной Галилея, как какого-то нового математического объекта со своим самостоятельным физическим смыслом, излишне. В рамках релятивистских же представлений рассмотрение производной Галилея бессодержательно по причине бессодержательности самих преобразований Галилея (в отличие от преобразований Лоренца). Но гиперконтинуальные представления о пространстве и времени делают использование галилеевой производной весьма востребованным, а равенство (6) – ложным.
Применим производную Галилея к электродинамике. В отсутствие свободных зарядов и токов, в изотропных и однородных средах без дисперсии интегральная форма закона индукции Фарадея и теоремы о циркуляции магнитного поля в лабораторной системе отсчета имеет вид (ε, μ, c, s, l – диэлектрическая и магнитная проницаемость, скорость света в вакууме, произвольная двумерная открытая поверхность и ограничивающий ее замкнутый контур, не обязательно совпадающий с электрическим контуром):
,
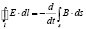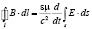. (7)
Эти два закона имеют взаимно симметричный вид с точностью до скалярного множителя, в силу чего их анализ идентичен. Рассмотрим более подробно, например, первый закон. В опытах Фарадея экспериментально установлено, что в контуре возникают одинаковые токи независимо от того, движется ли этот контур относительно токонесущего контура или же он покоится, а движется токонесущий контур, лишь бы их относительное движение в обоих случаях было одинаковым (галилеева инвариантность закона Фарадея). Поэтому поток через контур может изменяться вследствие изменения магнитного поля во времени, а также из-за того, что при перемещении контура изменяется положение его границы [2]. Соответствующее обобщение законов (7) на случай контура, движущегося в лабораторной и покоящегося в субстанциональной системе отсчета, имеет вид:
,
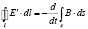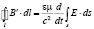, (8)
где E’ и B’ описывают поля в элементе dl в субстанциональной системе отсчета, то есть в такой инерциальной системе отсчета, в которой dl покоится; именно такое электрическое поле вызывает появление тока в случае наличия реального электрического контура в этом месте. Уравнения (8) весьма интересны и необычны с математической точки зрения, так как они связывают между собой полевые переменные в разных инерциальных системах отсчета (назовем такие уравнения транскоординатными). Именно использование транскоординатных уравнений позволяет адекватно описывать физические поля в гиперконтинууме. При этом в данном случае речь идет не просто о транскоординатности уравнений (8), а об их глобальной транскоординатности (связываемые ими инерциальные системы отсчета могут двигаться друг относительно друга с произвольной скоростью, а не обязательно бесконечно малой).
Уравнения (8) известны в классической электродинамике [2, 9]. Возникает вопрос, как перейти от уравнений в интегральной форме (8) к соответствующим уравнениям в дифференциальной форме наиболее адекватным физической реальности образом. В [2] на примере закона Фарадея сформулирован следующий подход: «Закон Фарадея можно записать также и в дифференциальной форме, если воспользоваться теоремой Стокса и считать контур покоящимся в выбранной системе отсчета (для того, чтобы E и B были определены в одной и той же системе отсчета)». Этот подход отвечает концепции инвариантности физического поля относительно скорости движения наблюдателя, предполагая простой отказ от транскоординатности уравнений посредством применения (2). Но если мы отвергаем данную концепцию, то должны отвергнуть и данный подход. Тем самым, дифференциальная форма соответствующих уравнений должна быть такой же транскоординатной, как и интегральная (8).
В соответствии с данным традиционным подходом, в [9] вводится операция дифференцирования по времени в движущейся (субстанциональной) системе отсчета, обозначаемая там через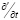 
. При этом негласно полагается, что в точке пространства, которая в субстанциональной системе отсчета имеет радиус-вектор r’, измерение полевой переменной в лабораторной системе отсчета равносильно ее измерению в той же самой субстанциональной системе отсчета. Но вне концепции инвариантности физического поля относительно скорости движения наблюдателя эти измерения не равносильны. Поэтому измерение нужно ограничивать лабораторной системой отсчета, не перенося его результаты на субстанциональную. Тем самым, мы приходим к производной Галилея (4), оставляющей уравнения электродинамики в дифференциальной форме глобально транскоординатными.
Результаты исследования и их обсуждение
Искомые глобально транскоординатные дифференциальные уравнения электродинамики, использующие галилееву производную, имеют вид:
, 
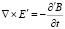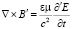. (9)
Они являются обобщением на случай несовпадения лабораторной и субстанциональной систем отсчета (v ≠ 0) известных дифференциальных уравнений Максвелла:
, 
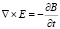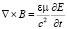. (10)
Векторным произведением оператора набла на обе части уравнений (10) с их взаимной подстановкой друг в друга получают известные волновые дифференциальные уравнения
, 
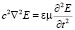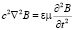. (11)
Их недостатком является отсутствие транскоординатности, они справедливы только в случае совпадения лабораторной и субстанциональной систем отсчета (v = 0). Аналогично, то есть векторным произведением оператора набла на обе части уравнений (9) с их взаимной подстановкой друг в друга, получим новые уравнения электродинамики – глобально транскоординатные волновые дифференциальные уравнения, использующие галилееву производную полевых функций и обобщающие уравнения (11) на случай v ≠ 0:
, 
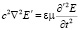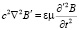. (12)
Исследуем более подробно уравнение вида (12) применительно к произвольным полевым функциям Ф(x, t) и Ф’(v, x’, t) и для случая плоской волны с волновым вектором, коллинеарным вектору v = (v,0,0) и осям OX, O’X’, координаты по которым задаются переменными x, x’. В этом случае уравнение оказывается одномерным, а полевые функции – скалярными:
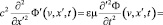
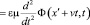. (13)
Если взять производную в правой части (13), это уравнение примет вид:
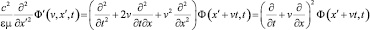. (14)
При v = 0 (13) и (14) вырождается в одномерный вариант волнового уравнения вида (11):
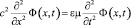. (15)
Любое решение (15) определяется надлежащей суперпозицией монохроматических волн
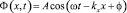(16)
с подходящими значениями параметров A ≥ 0, ω > , kx ≠ 0, φ∈ℝ – амплитуда, круговая частота, проекция волнового вектора на ось OX и начальная фаза волны. При этом все волны (16) должны иметь одну и ту же фазовую скорость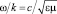 
, где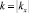 
– волновое число. Будем искать функцию Ф’(v, x’, t), удовлетворяющую (13)-(16), тоже в виде монохроматической волны, но с зависящими от v параметрами A’(v), ω’(v), kx’(v), φ’(v):
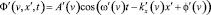, (17)
, 
, 
, 
, 
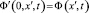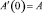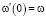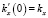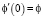. Подставим (16)-(17) в (14):
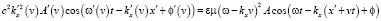. (18)
Приравнивая одноименные параметры волны в левой части (18) и волны в правой, имеем:
, 
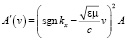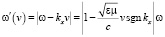, (19)
, 
, 
, 
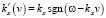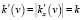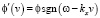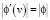. (20)
Таким образом, при переходе от лабораторной к субстанциональной системе отсчета изменяются амплитуда и частота (19) монохроматической волны, а ее волновое число и модуль начальной фазы (20) остаются неизменными. При этом частота изменяется таким образом, что фазовая скорость волны в субстанциональной системе отсчета получается по классическому правилу сложения скоростей из ее фазовой скорости в лабораторной системе отсчета и скорости субстанциональной системы отсчета относительно лабораторной:
,
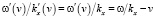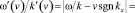
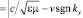. (21)
Из (19)-(21) видно, что если вектор фазовой скорости волны в лабораторной системе отсчета совпадает с вектором скорости субстанциональной системы отсчета в ней (kx > 0, v = ω/k), то в субстанциональной системе отсчета волна вообще исчезает (A’(v) = 0). Таким образом, в отличие от теории относительности, в теории гиперконтинуума такую волну всегда можно уничтожить подходящим выбором системы отсчета. Если же относительно лабораторной системы отсчета субстанциальная система отсчета перегоняет волну, то при переходе от лабораторной системы отсчета к субстанциональной направление распространения волны меняется на противоположное. Если в лабораторной системе отсчета волна распространяется в положительном направлении, то при переходе в субстанциональную она будет удовлетворять волновому уравнению (22), а если в отрицательном, то уравнению (23):
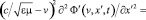
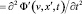; (22)
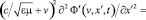
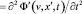. (23)
Выбор инерциальной системы отсчета на роль лабораторной, вообще говоря, условен. Так, субстанциальную систему отсчета можно в свою очередь принять за лабораторную, а в роли субстанциальной рассматривать некую третью (дважды штрихованную) инерциальную систему отсчета с направленной в ту же сторону, что и OX, O’X’, пространственной осью координат O’’X’’, координата по которой задается переменной x’’. Пусть, например, точка O’’ движется в положительном направлении оси O’X’ со скоростью Δv. Волна в новых лабораторной и субстанциональной системах отсчета будет иметь одинаковое волновое число и модуль начальной фазы и будет описываться полевыми функциями Ф’(v, x’, t) и Ф’(v + Δv, x’’, t) соответственно. Роль уравнения (15) будет играть (22) или (23), роль функции волны (16) – функция (17), а роль уравнений (22), (23) – следующие волновые уравнения:
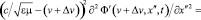
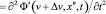; (24)
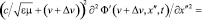
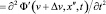. (25)
Для (24) роль равенств (19), (20) будут играть следующие преобразования параметров волны:
,
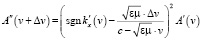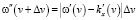, (26)
,
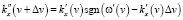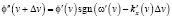. (27)
Для (25) соответствующие (26)-(27) преобразования параметров определяются аналогично.
Последовательный переход от не штрихованной к штрихованной и далее к дважды штрихованной системе отсчета равносилен непосредственному переходу от не штрихованной к дважды штрихованной. Например, при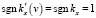 
из (19), (26) можно получить
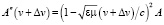, (28)
что получается и при непосредственном переходе к дважды штрихованной системе отсчета, так как (28) получается из (19) заменой v на v + Δv. В данном случае роль уравнения (14) будет играть следующее уравнение:
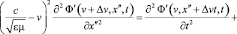
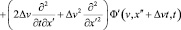. (29)
Для производных произвольного n-го порядка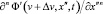 
и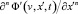 
можно использовать единое обозначение 
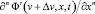и 
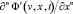соответственно (
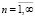), означающее просто производную по второму аргументу. В соответствии с этим после подстановки (22) в (29) получим:
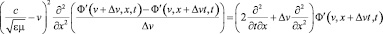. (30)
Пусть Δv →0. Введем еще одну новую производную, которую назовем транскоординатной и которая в случае одномерной системы пространственных координат имеет вид:
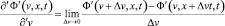. (31)
В определении (31) величины Ф’(v, x + Δvt, t) и Ф’(v + Δv, x, t) описывают физическое поле в одной и той же точке пространства, но в разных системах отсчета (штрихованной и движущейся относительно нее со скоростью Δv дважды штрихованной соответственно). В рамках концепции инвариантности поля относительно скорости движения наблюдателя они равны:
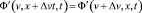, (32)
причем равенства (2) и (32) имеют одинаковый физический смысл, но применительно к разным парам систем отсчета. Однако вне рамок указанной концепции при переходе от штрихованной к дважды штрихованной системе отсчета полевая функция в данной точке пространства испытывает приращение, предел отношения которого к Δv при Δv →0 дает транскоординатную производную (31). Ее можно обобщить на случай высших порядков (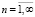
):
;
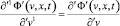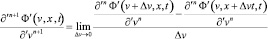. (33)
Используя транскоординатные производные первых двух порядков (33), можно представить приращение полевой функции в виде соответствующей частичной суммы ряда Тейлора:
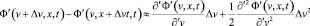. (34)
Подставляя (34) в (30), приравнивая между собой члены с одинаковыми степенями Δv в левой и правой частях получившегося равенства, устремляя Δv →0, учитывая то, что при этом Ф’(v, x + Δvt, t) → и Ф’(v, x, t) и добавляя равенство (22) в новой форме записи (с использованием переменной x вместо x’, получим следующую систему трех уравнений:
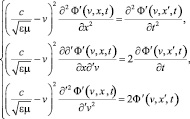(35)
Систему уравнений (35) можно записать в следующей проиндексированной по α форме:
, 
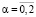(36)
или в операторной форме
۞Φ’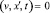
, (37)
где ۞=(۞ α);
۞ 
–
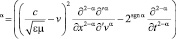подходящий вариант одномерного (случай одной оси пространственных координат) дифференциального оператора Дубровина, обобщающего оператор Даламбера □, который оказывается одной из трех (нулевой) его компонент для лабораторной системы отсчета, то есть α = 0, v = 0. Дифференциальное уравнение (36) или (37) есть гиперконтинуальное одномерное однородное волновое уравнение, обобщающее, подобно дифференциальному уравнению (13) или (14), известное одномерное однородное волновое уравнение (15). Принципиальное отличие между ними состоит в том, что (13)-(14) является глобально транскоординатной формой гиперконтинуального волнового уравнения, а (36)-(37) – его локально транскоординатной формой. Локальная транскоординатность означает, что уравнение связывает инерциальные системы отсчета, движущиеся друг относительно друга с бесконечно малой скоростью.
Транскоординатность гиперконтинуальных волновых уравнений обеспечивается использованием в них подходящих производных полевых функций. А именно, использование производной Галилея сообщает уравнению глобальную транскоординатность, а транскоординатной производной – локальную.
Заключение
Таким образом, мы предлагаем новый подход к развитию математического аппарата электродинамики в направлении более адекватного описания перехода от одной инерциальной системы отсчета к другой на основе гиперконтинуальных представлений о пространстве и времени за счет введения в рассмотрение глобально и локально транскоординатных уравнений, использующих новые галилееву и транскоординатную производные полевых функций, а также новый дифференциальный оператор Дубровина, обобщающий оператор Даламбера. Последовательное внедрение данного подхода в фундаментальные и прикладные научные исследования способно не только вывести на новый качественный уровень представления о пространстве и времени, но и открыть принципиально новые горизонты развития техники и технологий за счет открытия и освоения новых физических явлений и эффектов.