Scientific journal

International Journal of Applied and fundamental research

ISSN 1996-3955

ИФ РИНЦ = 0,593

Разработка численных алгоритмов решения краевых задач, описывающих процесс теплопроводности, продолжает оставаться актуальной задачей фундаментального и прикладного характера. Различные виды нелинейности описывающих этот процесс уравнений, которые обусловлены зависимостью коэффициента теплопроводности от параметров процесса, требуют разных подходов к решению. В данной работе рассматривается нелинейное параболическое уравнение

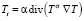, (1)

описывающее процесс теплопроводности в случае степенной зависимости коэффициента теплопроводности от температуры [2]. Здесь T = T(t, x) – температура, α > 0, σ > 0. Уравнение (1) стандартной заменой u = T^σ, t’ = αt сводится к уравнению

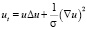. (2)

Важной особенностью уравнения (2) является вырождение параболического типа при u = 0. В данной работе рассматривается краевая задача для этого уравнения при заданном нулевом фронте тепловой волны, впервые сформулированная в работах А.Ф. Сидорова [6]. Численные алгоритмы для решения подобных задач в случае одной пространственной переменной разработаны ранее в работах [3, 4, 9]. Полученные в них результаты показывают эффективность применения метода граничных элементов (МГЭ) для решения задач на заданном конечном промежутке времени. Данная работа посвящена совершенствованию алгоритмов применения МГЭ на основе метода двойственной взаимности (МДВ). Смысл применения МДВ состоит в сведении интегралов по области решения задачи, возникающих вследствие нелинейности, к вычислениям на границе путем разложения по радиальным базисным функциям (РБФ). Оптимальный подбор системы РБФ и их параметров позволяет наиболее эффективно и точно решить задачу. В данной работе разработана программа, реализующая алгоритм решения задачи с применением МДВ, проведен анализ решения при различных системах РБФ, определена наиболее подходящая система и ее параметры.

Постановка краевой задачи

Рассматривается уравнение (2) в одномерном случае,

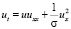, (3)

при краевом условии

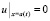. (4)

Предполагается, что 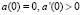. При наличии вырождения, не теряя общности рассмотрения, можно считать, что 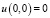. Условие (4) задает, таким образом, нулевой фронт тепловой волны. Задача состоит в определении функции 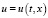в области , .

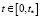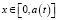Алгоритм решения МГЭ

Классический подход к решению уравнения параболического типа методом граничных элементов предполагает использование фундаментального решения, зависящего от времени [1], численное решение при этом строится по шагам по времени. Однако нелинейность и вид краевого условия (4), при котором область решения задачи (область ненулевых значений искомой функции) изменяется с течением времени, делает такое решение затруднительным. В связи с этим предлагается решать на каждом шаге по времени краевую задачу для уравнения эллиптического типа.

Можно показать, что при выполнении условия (4) справедливо соотношение

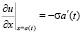. (5)

Представим в произвольный момент времени t уравнение (3) в виде

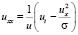. (6)

Граничные условия (4), (5) в момент t представим следующим образом:

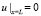, (7)

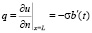, (8)

где L = a(t), n – вектор внешней нормали к границе рассматриваемой области, q – поток. Задачу (6) – (8) будем рассматривать как краевую задачу для уравнения Пуассона в области x∈[0, L]. Решение этой задачи методом граничных элементов для эллиптических задач теории потенциала [1] приводит к соотношению

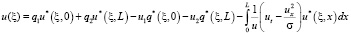, (9)

где 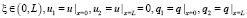, 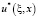– фундаментальное решение [1]:

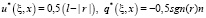. (10)

Здесь r = x – ξ, l – некоторое число (примем l = L). Переходя в уравнении (9) к пределам при ξ → 0 и ξ → L, получим систему граничных уравнений

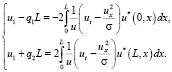(11)

в которой u₁ и q₁ являются неизвестными, а q₂ задано граничным условием (8). Итерационное решение системы (11), предполагающее подстановку в правые части искомой функции, полученной на предыдущей итерации, определит значения u₁ и q₁, а следовательно, и решение (9) в рассматриваемый момент времени в области .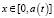

Для вычисления интегралов, стоящих в правых частях уравнений (11), применим метод двойственной взаимности [10]. Представим входящий в подынтегральные выражения множитель 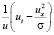в виде

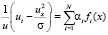, (12)

где для функций f_i существуют такие функции 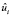, что 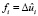. В качестве функций f_i применяются радиальные базисные функции, значения которых зависят от расстояния между текущей точкой и заданными точками коллокации x₁, x₁,…, x_n, лежащими на отрезке [0, L]: .

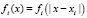С учетом (12), интегралы могут быть вычислены следующим образом:

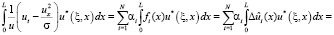
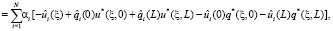(13)

где 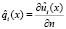. Все вычисления, таким образом, сводятся на границу области решения задачи, и основное преимущество МГЭ – уменьшение размерности задачи – сохраняется. Полученные соотношения позволяют решить исходную задачу (3), (4) следующим образом. На каждом шаге по времени, t = t_k = kh, где h – величина шага, решаем задачу для отрезка [0, L], L = a(t_k), с граничными условиями u₂ = 0, 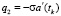, используя метод простых итераций:

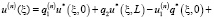
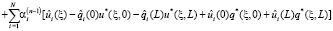, (14)

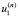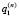где и – решение системы система уравнений, полученной из (11):

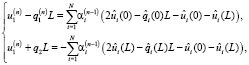(15)

а коэффициенты 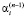определяются из системы линейных уравнений

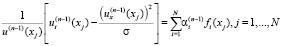, (16)

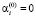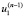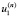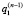записанной для предыдущей итерации. Отметим, что . Итерационный процесс заканчивается на n-й итерации, если значения и , и 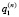достаточно близки.

Сравнение решения МГЭ и точного решения

Ключевым вопросом эффективности представленного алгоритма является выбор системы РБФ и их параметров, наиболее подходящих для рассматриваемого класса задач. Для анализа применения различных видов РБФ построенный алгоритм был реализован в виде программы. Анализ проводился на основе сравнения результатов расчетов с известными точными решениями задачи вида

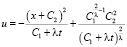, (17)

где 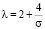, C₁ и C₂ – положительные константы [5]. Нулевой фронт, соответствующий этому решению, имеет вид

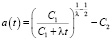. (18)

В качестве факторов анализа были приняты вид РБФ, их параметры, связанные с расположением точек коллокации, и шаг по времени.

Рассматривались три системы РБФ: полигармонические сплайны (ПС) 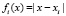; функции Гаусса 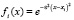; мультиквадрики 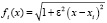. Целью анализа было подобрать систему РБФ и значения параметра формы ε, при которых решение по предложенному алгоритму наиболее близко к точному.

Результаты расчетов при различных значениях параметров C₁ и C₂ хорошо согласуются с точным решением (17). Приведенные ниже результаты были получены при характерных значениях σ = 3, C₁ = 10, C₂ = 1.

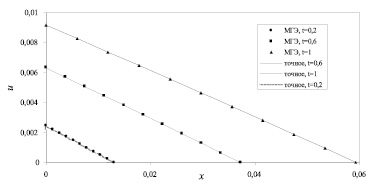
Полученные решения при различных РБФ и значениях параметров достаточно близки. Для примера на рисунке приведено сравнение точного решения и решения, полученного при использовании ПС, с шагом по времени h = 0,05.

Во всех вариантах расчетов наибольшее отклонение численного решения от точного в различные моменты времени наблюдалось при х = 0, что вполне соответствует виду краевого условия (4). Поэтому в качестве оценки точности численного решения мы использовали его отклонение от точного в этой точке. Результаты оценки точности решения приведены в табл. 1–3. В табл. 1 приведены значения и отклонения от точного решения при х = 0 в некоторые моменты времени для решений, полученных при использовании ПС, с шагами по времени h = 0,1 и h = 0,05. В табл. 2 и 3 приведены аналогичные результаты, полученные соответственно при использовании функций Гаусса и мультиквадриков с различными значениями параметра формы. В качестве базовых значений параметра формы были приняты значения 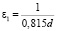, где 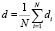, di – расстояние от i-й точки коллокации до ближайшей другой [8], и 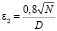, где D – диаметр наименьшего круга, содержащего все точки коллокации [7].

Таблица 1

Отклонение решения МГЭ с использованием полигармонических сплайнов от точного решения при х = 0

Сравнение решения МГЭ и точного решения

Таблица 2

Отклонение решения МГЭ с использованием функций Гаусса от точного решения при х = 0

Таблица 3

Отклонение решения МГЭ с использованием мультиквадриков от точного решения при х = 0

Анализ результатов и выводы

Проведенные расчеты показали, что точность решения возрастает с уменьшением шага по времени, что свидетельствует об устойчивости разработанного алгоритма. Сравнение результатов использования разных систем РБФ позволяет делать следующие выводы. Полигармонические сплайны, не зависящие от параметра формы, обеспечивают высокую точность решения, что говорит об их универсальности. Решения, полученные с использованием мультиквадриков при любых значениях параметра формы, имеют заметно меньшую точность, чем при использовании ПС. Более высокую по сравнению с ПС точность можно обеспечить использованием функций Гаусса с параметром формы, принадлежащим интервалу ε∈[ε₂; ε₁]. Наибольшая точность достигается при ε∈[0,5ε₁; 2ε₂].

Таким образом, применение метода двойственной взаимности позволяет с высокой точностью решать задачи вида (3) – (4) на конечном промежутке времени. Полученные результаты будут использованы для разработки алгоритмов решения аналогичных задач большей размерности.

Работа выполнена при поддержке программы фундаментальных научных исследований УрО РАН, проект № 15-7-1-17.