При рассмотрении процессов падения тела или скольжения тела без
трения вниз по наклонной плоскости используется закон сохранения механической
энергии в виде: 
, где h -
первоначальная высота тела над поверхностью Земли, Vk- конечная скорость. Обозначим длину наклонной
плоскости S, а угол её
наклона к горизонту - α, тогда h=S∙sinα. В соответствии с законом
сохранения энергии, конечная скорость будет одна и та же: и в случае
вертикального падения, и в случае скольжения по наклонной плоскости: 
и т.д. Говорят,
что сила тяжести во всех случаях совершила одну и ту же работу mgh. Представим себе, что
угол α очень мал. Тогда тело окажется на значительном удалении от места
вертикального падения. При этом оно будет обладать точно такой же кинетической
энергией, как и при вертикальном падении. При скольжении по наклонной плоскости
тело не только спускается к Земле, но и совершается работа перемещения на
значительное расстояние. Работа при скольжении должна быть больше работы при
вертикальном падении.
При движении тела без трения по наклонной плоскости сила тяжести P=mg может быть разложена на две
составляющие: скатывающую силу Fα=mg sinα и нормальную реакцию опоры N=mg cosα. Квадрат времени скольжения по наклонной плоскости равен
.
Работа скатывающей силы
Её можно выразить через импульс скатывающей силы Ia=Fatk
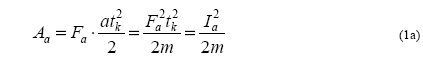
Работу нормальной силы запишем через импульс силы IN=Ntk
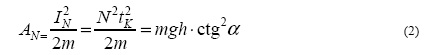
Т.к. силы Fa и N ортогональны, то работы этих сил аддитивны. Тогда суммарную работу этих сил можно найти арифметическим сложением
:
. При угле α=10º работа силы тяжести A∑≈33mgh.
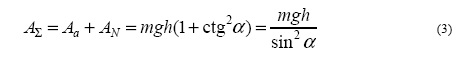
Если наклонная плоскость шероховата, то движение происходит с
некоторым коэффициентом трения
. Будем рассматривать случай самопроизвольного
скольжения тела
(μ<tgα). В этом
случае равноускоренное скольжение вниз будет происходить под действием силы Fa=mg(sinα - μcosα). Время скольжения.
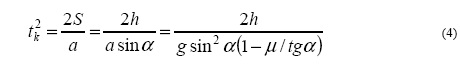
Скорость в конце наклонной плоскости
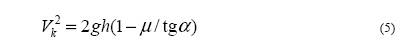
Работа, совершаемая силой тяжести, при скольжении с трением по наклонной поверхности.
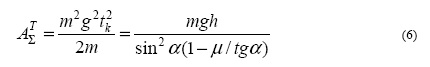
При коэффициенте трения μ=0 получаем соотношение (3). Отношение работы с трением A∑T к работе силы тяжести A∑ при отсутствии трения в зависимости от отношения μ/tgα приведены в таблице 1.
Таблица 1
|
μ/tgα |
0 |
0,2 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
|
A∑T/ A∑ |
1 |
1,25 |
1,667 |
2 |
2,5 |
3,33 |
5 |
10 |
20 |
При коэффициенте трения μ = 0,9tα и угле α=10º работа
силы тяжести
.
Более подробный вывод формул для вычисления работы различных сил приведен в [1,2].
Список литературы
1. Иванов Е.М. Работа и энергия в классической механике и первый закон термодинамики. Димитровград: ДИТУД УлГТУ, 2004.
2. Ivanov E.M. Work of centripetal and gyroscopic Forces.//European Journal Natural History, 2006, #1, p.80.