Рассматривается нестационарная нелинейная дескрипторная система
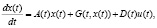(1)
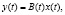(2)
где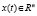 
– функция состояния, 
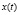– управление, 
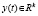– измеряемая выходная функция, коэффициенты 
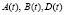– матрицы соответствующих размеров, нелинейное слагаемое 
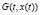устанавливает соответствие между компонентами вектор функции 
, 
(
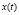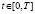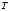– конечно или бесконечно). Наблюдаемая система (1), (2) сводится за конечное число шагов к эквивалентной системе с элементами меньшей размерности. Указанный метод ранее применялся при решении задач с контрольными точками, при исследовании полной наблюдаемости и полной управляемости различных систем, жесткости дескрипторных динамических систем, инвариантности систем относительно различных возмущений ([1 – 4]).
Итогом поэтапной декомпозиции исходной системы является построение функции управления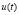 
и состояния 
.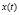