В современном мире цифровых технологий каналы передачи данных и носители информации остаются далекими от совершенства. Магнитные и оптические носители информации чувствительны к физическим повреждениям, делающим невозможным чтение информации из отдельных участков на поверхности носителя. Кабельные и беспроводные линии передачи информации подвержены воздействию внешних помех, искажающих форму передаваемых сигналов и тем самым делающих невозможным однозначное распознавание информации на стороне приемника.
В настоящее время в системах хранения и передачи данных применяют различные технологии информационного резервирования с применением специальных алгоритмов кодирования на базе корректирующих кодов, в частности, кодов Рида-Соломона [1], которые за счет использования избыточной информации делают возможным исправление искажений. Однако, алгоритмы кодирования и декодирования информации с применением кодов Рида-Соломона достаточно нетривиальны, и для эффективной программной или аппаратной реализации требуется достаточно глубокая математическая проработка с применением алгебры конечных полей Галуа [2]. В частности, алгоритм декодирования состоит из блока вычисления синдрома искажений, полинома локаторов искажений, самих локаторов искажений и значений искажений, и все блоки имеют дело с полиномами, заданными над конечным полем Галуа. Особое место занимает блок вычисления значений искажений на базе метода Форни, использующего усеченную свертку полиномов, заданных над полем Галуа, и здесь требуется особый подход для построения эффективного алгоритма вычисления значения усеченной свертки полиномов при заданном аргументе.
В рамках научных исследований автора в области надежности систем хранения, передачи и обработки данных [3-9], а также в области информационного резервирования [10] возникла научная задача разработки эффективного алгоритма вычисления усеченной свертки полиномов Ψ(х) и ξ(х), заданных над полем Галуа GF(pm), при заданном аргументе x, и аппаратной реализации для поля Галуа GF(2m).
Полином над полем Галуа. Пусть задано поле Галуа GF(pm). Тогда полиномом, заданным над полем Галуа, будем называть функцию:
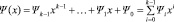 ;
;
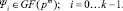 (1)
(1)
Над полиномами можно производить алгебраические операции, также на место переменной x можно подставлять конкретное значение, являющееся элементом поля Галуа GF(pm), и вычислять значение функции. При пересчете коэффициентов полинома при выполнении операции или вычислении значении функции, строго соблюдаются правила арифметики для поля GF(pm).
Сумма полиномов. Сложение полиномов выполняется путем сложения по правилам арифметики поля Галуа GF(pm) соответствующих коэффициентов, стоящих перед переменной в одной степени. Отсутствующие в полиномах коэффициенты, считаются равными нулю.
Пусть заданы два полинома Ψ(х) и ξ(х). Тогда, сумма этих полиномов определяется следующим образом:
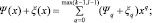
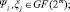
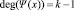 ;
;
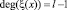 . (2)
. (2)
Пример. Сложим полиномы Ψ(х) = 49x2 + 50x + 51 и ξ(х) = 19x2 + 93x + 1, заданные над полем GF(28), заданного с помощью неприводимого многочлена p(х) = x8 + x4 + x3 + x3 + 1. Используя арифметику поля GF(28) для сложения коэффициентов полиномов, имеем: (49 + 19)x2 + (50 + 93)x + (51 + 1) = 34x2 + 111x + 50.
Произведение полиномов. Умножение полиномов осуществляется путем вычисления суммы результатов умножения одного полинома на каждый член другого полинома. Соответственно, степень результирующего полинома равна сумме степеней перемножаемых полиномов.
Пусть заданы два полинома Ψ(х) и ξ(х). Тогда, произведение этих полиномов определяется следующим образом:
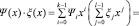
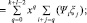
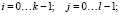
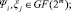
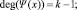
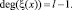 (3)
(3)
Пример. Умножим полиномы Ψ(х) = 49x2 + 50x + 51 и ξ(х) = 19x2 + 93x + 1, заданные над полем GF(28), заданного с помощью неприводимого многочлена p(х) = x8 + x4 + x3 + x3 + 1. Используя арифметику поля GF(28) для сложения и умножения коэффициентов полиномов, получаем: Ψ(х)∙ξ(х) = (49∙19)x4 + (49∙93 + 50∙19)x3 + (49∙1 + 50∙93 + 51∙19)x2 + (50∙1 + 51∙93)x + 51∙1 = 100x4 + 218x3 + 31x2 + 3x + 51.
Особо отметим, что если мы будем подразумевать, что любые «отсутствующие» коэффициенты в полиномах, в том числе коэффициенты с индексами больше степени полиномов, равны нулю: 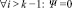 и
и 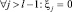 , то мы внутреннее суммирование по двум индексам можем преобразовать суммирование по одному индексу. Для этого мы изменим верхние границы для обоих индексов: i ≤ q и j ≤ q, при этом мы ничего не теряем, поскольку i ≥ 0, j ≥ 0 и i + j = q. Случаи, когда i > q (при k – 1 > q), или j > q (при l – 1 > q), все равно никогда не пройдут условие i + j = q, так как i ≥ 0 и j ≥ 0. А при i > k – 1 (при q > k – 1) коэффициенты Ψi = 0, а при j > l – 1 (при q > l – 1) коэффициенты ξj = 0. Тогда в итоге мы получаем следующие три условия: i + j = q, 0 ≤ i ≤ q и 0 ≤ j ≤ q.
, то мы внутреннее суммирование по двум индексам можем преобразовать суммирование по одному индексу. Для этого мы изменим верхние границы для обоих индексов: i ≤ q и j ≤ q, при этом мы ничего не теряем, поскольку i ≥ 0, j ≥ 0 и i + j = q. Случаи, когда i > q (при k – 1 > q), или j > q (при l – 1 > q), все равно никогда не пройдут условие i + j = q, так как i ≥ 0 и j ≥ 0. А при i > k – 1 (при q > k – 1) коэффициенты Ψi = 0, а при j > l – 1 (при q > l – 1) коэффициенты ξj = 0. Тогда в итоге мы получаем следующие три условия: i + j = q, 0 ≤ i ≤ q и 0 ≤ j ≤ q.
Заметим, что оба индекса неотрицательны и ограничены одним и тем же верхним пределом, причем сумма индексов также равна верхнему пределу. Тогда, очевидно, можно избавиться от одного из индексов, попросту выразив его через другой: j = q – i, и мы ничего не теряем, поскольку 0 ≤ q – i ≤ q, так как 0 ≤ i ≤ q.
В итоге мы получаем следующую «оптимизированную» формулу произведения:
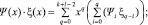
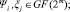
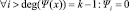 ;
;
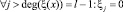 . (4)
. (4)
Усеченная свертка полиномов. Пусть заданы два полинома Ψ(х) и ξ(х). Тогда, усеченной линейной сверткой полиномов будем называть остаток от произведения этих полиномов по модулю полинома xr, иными словами 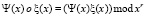 .
.
По сути, усеченная линейная свертка – это произведение полиномов, в котором «отброшены» члены, степень переменной x в которых больше либо равна r:
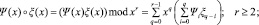
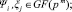
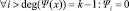
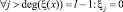 . (5)
. (5)
Пример. Найдем усеченную свертку полиномов Ψ(х) = 49x2 + 50x + 51 и ξ(х) = 19x2 + 93x + 1, заданных над полем GF(28), по модулю полинома x2. Получаем:
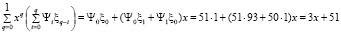 .
.
Вычисление значения усеченной свертки полиномов при заданном аргументе над полем Галуа GF(pm). Выше мы определили, что усеченная свертка Ω(х) двух полиномов Ψ(х) и ξ(х), заданных над полем Галуа GF(pm), и при заданном r, определяется как:
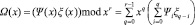 .
.
Нетрудно заметить, что вычисление значения полинома-свертки при заданном аргументе по вышеприведенной формуле в общей сложности требует 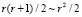 итераций для вычисления двойной суммы. Выполним ряд преобразований формулы:
итераций для вычисления двойной суммы. Выполним ряд преобразований формулы:
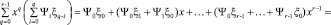
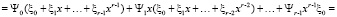
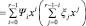 .
.
Преобразуем формулу для использования рекуррентной схемы вычисления:
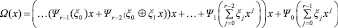 .
.
Тогда, в первом приближении имеем следующую итерационную схему вычисления значения полинома-свертки Ω(х) при заданном аргументе х*:
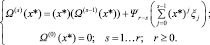 (6)
(6)
Заметим, что хотя и итерационная процедура вычисляет Ω(х*) за r итераций, но на каждой итерации, требуется вычисление суммы 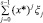 , количество слагаемых в которой с каждой итерацией s = 1…r только растет. Однако заметим, что количество слагаемых в сумме в точности совпадает с номером итерации, и можно не заново пересчитывать сумму на каждой итерации s, а лишь добавлять очередное слагаемое к сумме, вычисленной на предыдущей итерации s 1. Обозначив
, количество слагаемых в которой с каждой итерацией s = 1…r только растет. Однако заметим, что количество слагаемых в сумме в точности совпадает с номером итерации, и можно не заново пересчитывать сумму на каждой итерации s, а лишь добавлять очередное слагаемое к сумме, вычисленной на предыдущей итерации s 1. Обозначив 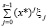 , имеем рекуррентное соотношение:
, имеем рекуррентное соотношение: 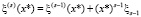 , причем
, причем 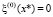 . Очевидно, можно совместить обе итерационные схемы, на каждой итерации вычисляя сначала очередную
. Очевидно, можно совместить обе итерационные схемы, на каждой итерации вычисляя сначала очередную 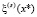 , используя
, используя 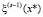 , а затем и
, а затем и 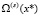 , используя
, используя 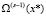 и
и 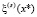 . Наконец, отметим, что для вычисления
. Наконец, отметим, что для вычисления 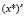 также необязательно на каждой итерации возводить аргумент х* в степень s, можно использовать соотношение
также необязательно на каждой итерации возводить аргумент х* в степень s, можно использовать соотношение 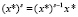 , причем
, причем 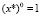 . Тогда, имеем «оптимизированную» итерационную схему вычисления значения полинома-свертки Ω(х) при заданном аргументе х*:
. Тогда, имеем «оптимизированную» итерационную схему вычисления значения полинома-свертки Ω(х) при заданном аргументе х*:
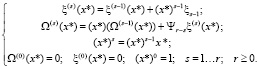 (7)
(7)
Пример. Вычислим значение свертки полиномов Ψ(х) = 49x2 + 50x + 51 и ξ(х) = 19x2 + 93x + 1, заданных над полем GF(28), по модулю полинома x2 (т.е. r = 2) при заданном аргументе x* = 64, используя итерационную схему.
Имеем следующие начальные значения: 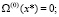
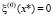 ;
; 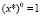 .
.
Далее, на итерации s = 1 выполняем следующие вычисления:
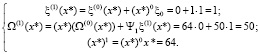
Наконец, на итерации s = 2 (последняя итерация) получаем:
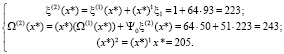
Тогда, искомое значение свертки полиномов равно 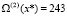 .
.
Для проверки полученного значения, подставим заданный аргумент x* = 64 в полином-свертку 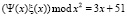 , полученный в рассмотренном выше примере для полиномов Ψ(х) = 49x2 + 50x + 51 и ξ(х) = 19x2 + 93x + 1. Имеем: 3∙64 + 51 = 243. Таким образом, очевидно, результат вычисления по рекуррентной схеме верен.
, полученный в рассмотренном выше примере для полиномов Ψ(х) = 49x2 + 50x + 51 и ξ(х) = 19x2 + 93x + 1. Имеем: 3∙64 + 51 = 243. Таким образом, очевидно, результат вычисления по рекуррентной схеме верен.
Аппаратная реализация для поля Галуа GF(2m). Теперь рассмотрим аппаратную реализацию вычисления значения полинома-свертки Ω(х) при заданном аргументе х* над полем Галуа GF(2m). Аппаратная реализацию можно построить при помощи трех m-битных регистров, а также двух сумматоров и четырех умножителей элементов поля Галуа GF(2m). Аппаратная реализация быстрых сумматоров и умножителей элементов поля Галуа GF(2m) хорошо освещены в литературе [1, 2].
Ниже на рисунке представлена предлагаемая автором функциональная схема вычислителя значения полинома-свертки Ω(х) при заданном аргументе х*.
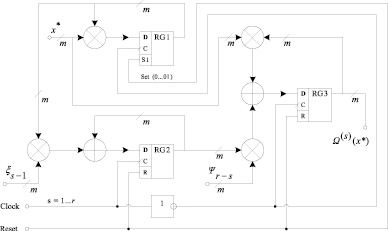
Функциональная схема последовательного вычислителя значения полинома-свертки 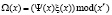 при заданном аргументе х*
при заданном аргументе х*
Регистр RG1 используется для хранения вычисленного на предыдущей итерации степени аргумента 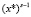 , регистр RG2, соответственно,
, регистр RG2, соответственно, 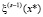 , наконец, в регистре RG3 хранится
, наконец, в регистре RG3 хранится 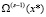 . Перед началом работы по сигналу сброса, поступающего на вход Reset, регистр RG1 устанавливается в значение (0…01), соответствующее элементу «1» поля
. Перед началом работы по сигналу сброса, поступающего на вход Reset, регистр RG1 устанавливается в значение (0…01), соответствующее элементу «1» поля 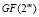 , а регистры RG2 и RG3 сбрасываются в нулевое значение.
, а регистры RG2 и RG3 сбрасываются в нулевое значение.
Далее на вход Clock поступают тактовые сигналы в течение итераций s = 1…r. Особо отметим, что вход синхронизации (С) регистра RG2 подключен к Clock напрямую, и, соответственно, регистр принимает информацию со своего информационного входа (D) по фронту тактового сигнала. Что же касается регистров RG1 и RG2 то они принимают информации по спаду тактового сигнала, так как и входы синхронизации подключены к Clock через инвертор.
Такая «двухтактная» синхронизации регистров позволяет на каждом такте s = 1…r сначала вычислять и записывать в регистр RG2 значение 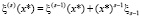 , и только потом вычислять и записывать
, и только потом вычислять и записывать 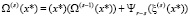 в регистр RG1, и одновременно с этим также вычислять и записывать очередную степень аргумента
в регистр RG1, и одновременно с этим также вычислять и записывать очередную степень аргумента 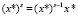 в регистр RG3, и таким образом, соблюдать правильную «очередность» вычислений на каждом такте.
в регистр RG3, и таким образом, соблюдать правильную «очередность» вычислений на каждом такте.
В результате за r тактов схема вычисляет искомое значение полинома-свертки 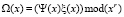 при аргументе х*.
при аргументе х*.
Заключение
Таким образом, в рамках данной статьи рассматривается алгоритм вычисления усеченной свертки полиномов над полем Галуа. В статье приведено определение полинома, усеченной свертки полиномов и формула для ее вычисления над полем Галуа GF(pm). Также в статье рассматривается алгоритм вычисления значения усеченной свертки полиномов над полем Галуа GF(2m) при заданном аргументе и предлагаемая автором аппаратная реализация алгоритма.
Полученные результаты были использованы автором для разработки обучающей программы и лабораторных стендов для изучения студентами технических специальностей технологии кодирования информации при применении кодов Рида-Соломона.

